DBRX, Continual Pretraining, RewardBench, Faster Inference, and More
A deep dive into recent and impactful advancements in LLM research...
If you like the newsletter, feel free to subscribe below, get in touch, or follow me on Medium, X, and/or LinkedIn.
Research on large language models (LLMs) is evolving rapidly. Recently, even models and techniques that have achieved state-of-the-art performance for long durations of time are being quickly dethroned. For example, GPT-4 was (arguably) surpassed by Claude-3, while DBRX replaced Mixtral as the highest-performing open LLM. Within this overview, we will take an in-depth look at numerous recent advancements in LLM research, including:
New models like DBRX and Jamba (and new architectures!).
Dynamic training algorithms that allow us to efficiently train LLMs over expanding and evolving datasets to eliminate knowledge cutoffs.
Benchmarks that give us a new understanding of how LLMs function.
Faster decoding algorithms that increase the inference speed of LLMs by more than 10×.
Although these advancements address a wide set of topics, they work towards a unified goal—making LLMs more practical to train and use. By releasing new models, evaluating those models, developing better training algorithms, and devising more cost-efficient hosting methods, we are exploring new avenues of making LLMs more performant in terms of accuracy or cost. Given the staggering pace of LLM research, the practical effectiveness of these models is beginning to improve exponentially as research continues to progress towards this unified goal.
🧱DBRX🧱: A New State-of-the-Art Open LLM [21]
DBRX is the next model in the series of Open LLMs released by Mosaic. Two versions of the model are released—a base model (DBRX base) and a finetuned model (DBRX Instruct)—under an open license (i.e., the Databricks open model license). Mosaic entered the space of open LLMs with their proposal of MPT-7B in May of 2023—less than a year ago! Since then, Mosaic has been acquired for $1.3B, trained thousands of specialized LLMs for customers, and still found time to release several open LLMs—DBRX being the latest—and improve the end-to-end efficiency of LLM pretraining by over 4×. The MoE-based DBRX model achieves new state-of-the-art performance for open language models in terms of both quality and efficiency across a massive suite of evaluations.
Model architecture. DBRX is a Mixture-of-Experts (MoE) model that is pretrained on 12T tokens1 of curated text. Compared to popular models like ST-MoE [23] that use a smaller number of large experts, DBRX takes an opposite strategy, using a fine-grained MoE architecture with a larger number of small experts. The model has 132B parameters in total with 36B parameters active at any given time (i.e., each MoE layer has 16 experts in total and four experts are chosen in each forward pass). Relative to models like Mixtral and Grok-1 that have only eight experts (and two active experts), DBRX has 65× more potential combinations of experts that can be used, which is found to improve model quality. Notably, MoE models are hard to train (and finetune) due to instabilities that arise during training and communciation bottlenecks. However, Mosaic has created a robust and repeatable recipe for efficiently training such models.
“We estimate that our new pretraining data is at least 2x better token-for-token than the data used to train MPT-7B. In other words, we estimate that half as many tokens are necessary to reach the same model quality.” - from [21]
More DBRX details. Although the pretraining dataset for DBRX is much larger than prior models, authors in [21] also claim that the data used to train DBRX is higher-quality2. As a result of this quality increase, the statistical training efficiency of DBRX is higher than normal—training is faster because we achieve higher accuracy with fewer tokens. Additionally, a curriculum learning strategy— meaning that the data mixture is dynamically changed throughout pretraining—is adopted for training DBRX and found to improve model quality.
DBRX has a longer context length of 32K and uses the GPT-4 tokenizer3 (available via tiktoken) instead of the GPT-NeoX tokenizer used by prior MPT models. According to researchers at Mosaic, the GPT-4 tokenizer was selected partly due to performance and partly due to the practical consideration that it makes pricing comparisons to competing models (i.e., GPT-4) more direct/simple.
Better efficiency. The proposal of DBRX comes with large improvements in terms of both training and inference efficiency. As mentioned above, DBRX is trained over an optimized dataset that improves training efficiency by roughly 2×. However, a variety of other factors yield further boosts in training efficiency:
The MoE architecture, which is found in smaller-scale experiments (i.e., on DBRX MoE-B, a 23.5B parameter model with 6.6B active parameters) to require 1.7× fewer FLOPS during training compared to a performance-matched LLaMA-2-13B model.
Other modifications to the decoder-only architecture (i.e., RoPE, GLU activation, and GQA).
“Better optimization strategies” (hopefully more details coming soon).
When considering all data, architecture, and optimization changes, the end-to-end training process of DBRX requires 4× less compute than prior models released by Mosaic. To determine this number, authors in [21] compare a smaller variants of DBRX, DBRX MoE-A (i.e., a 7.7B parameter LLM with 2.2B active parameters) to MPT-7B, finding that DBRX MoE-A achieves similar performance on the Databricks Gauntlet while using 3.7× fewer FLOPS during training.
DBRX also comes with improvements to inference efficiency—up to 2× faster than LLaMA-2-70B at 150 tokens per second per user in load tests. Mosaic has an optimized serving infrastructure that uses TensorRT-LLM and 16 bit precision, which is very fast (try it out here). The MoE architecture of DBRX also aids inference efficiency due to the relatively low number of active parameters. For example, DBRX is 40% of the size of Grok-1 in both total and active parameters.
“Using an MoE architecture makes it possible to attain better tradeoffs between model quality and inference efficiency than dense models typically achieve.” - from [21]
Empirical evaluation. In comparison to other open LLMs, we see that DBRX Instruct achieves the best performance on composite benchmarks by a large margin compared to Mixtral; see below. Notably, DBRX has impressive programming skills, outperforming models like Grok-1 that are more than twice its size and specialized coding models like CodeLLaMA-70B (despite being a general-purpose LLM!). DBRX also performs well on reasoning/math tasks4.
Compared to closed models, DBRX surpasses the performance of GPT-3.5 and is competitive with Gemini Pro. Gemini Pro only outperforms DBRX on GSM8K, while Mixtral-Medium performs better on a select few tasks that are considered; see below. At a high level, DBRX seems to be good at general knowledge and commonsense reasoning tasks, as well as programming and math. DBRX is also shown in [21] to perform competitively with models like Mixtral and GPT-3.5/4-Turbo on tasks involving RAG and long context.
The research process. Although my take is definitely biased, Mosaic has one of the best (if not the best) LLM research teams in the world. DBRX was created in less than three months using a cluster of 3K H100 GPUs with a budget of around $10M. Mosaic is an applied research team, meaning that a lot of their work is customer-focused—they have trained thousands of specialized LLMs for various Databricks customers. However, this focus upon applications is exactly what makes the team so interesting—it forces researchers to sift through the noise of AI research and find techniques that work. Plus, the team still finds enough free time to conduct legitimate research and has had a massive impact on the trajectory of open-source LLMs through the MPT/DBRX models. For more details on Mosaic’s research team and the building of DBRX, check out the awesome article below.
Competing LLMs. Almost immediately after the release of DBRX, several companies responded by releasing new models of their own:
xAI released Grok-1.5 [link]
AI21 release Jamba [link]
Qwen released Qwen1.5-MoE [link]
SambaNova released Samba-CoE v0.2 [link]
The Samba-CoE model has received a lot of pushback for claiming to outperform DBRX because i) the model is not released openly and ii) it is a composition of experts (CoE) model, or an ensemble of multiple LLMs with output coordinated via a (proprietary) router. In other words, this is a complete “apples-to-oranges” comparison, but Samba-CoE v0.2 does seem to perform well (see below) and is fast (i.e., 330 tokens per second) despite being a CoE.

Qwen1.5-MoE [25] is a smaller MoE model that has 14.3B total parameters and 2.7B active parameters. This model is competitive with similarly-sized state-of-the-art dense models like Mistral-7B or Gemma-7B. Compared to the prior Qwen1.5-7B dense model, Qwen’s MoE model achieves a 75% decrease in training costs and has 1.74× faster inference. Similarly to DBRX, Qwen1.5-MoE uses fine-grained experts, but each MoE layer has a larger number of experts—64 for each layer instead of 16. Interestingly, four of these experts are set to always be active during any forward pass. Additionally, a custom weight initialization strategy is used that begins by re-purposing the weights of Qwen-1.8B for the MoE model (with some added randomness), which authors find to improve convergence speed. Despite its smaller size, Qwen1.5-MoE performs quite well; see below.
Grok-1.5—which is a followup to the open release of Grok-1, a 304B parameter (~76B active) MoE with open weights—is (unfortunately) not an open model, but it will be available on X in the near future. The model comes with an expanded context length (128K tokens), as well as improved capabilities on reasoning, math, and coding tasks; see below. Despite the longer context, Grok-1.5 achieves nearly perfect results on the needle in the haystack test—a benchmark commonly used to determine how well an LLM pays attention to a large context window.

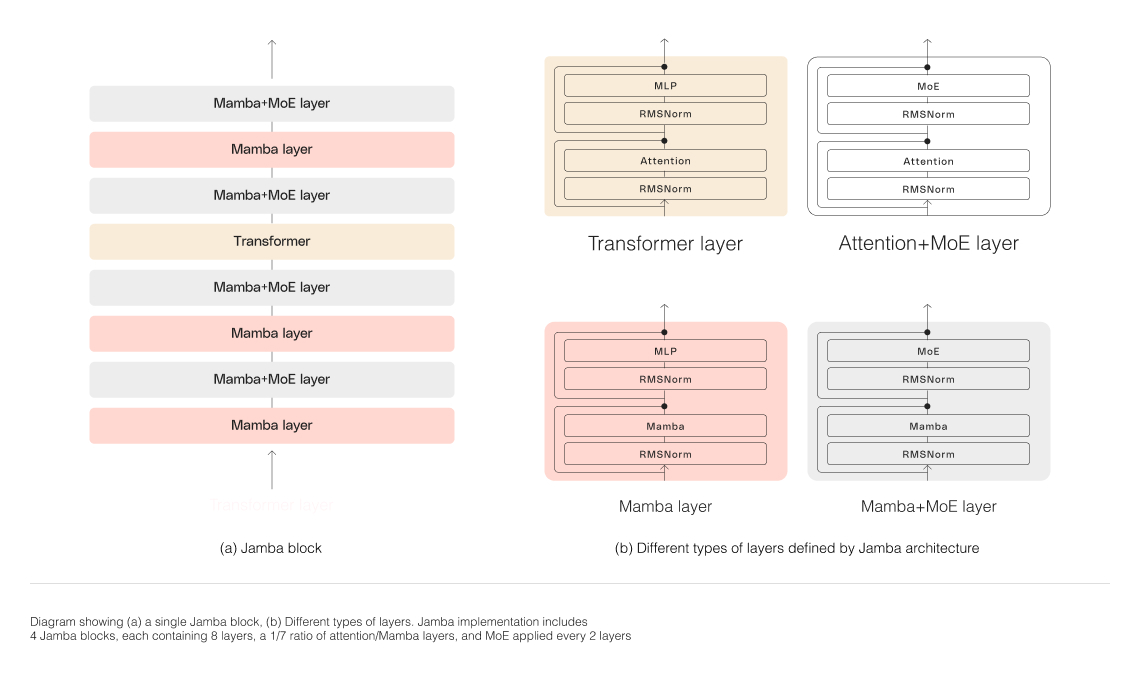
“Each Jamba block contains either an attention or a Mamba layer, followed by a multi-layer perceptron (MLP), producing an overall ratio of one Transformer layer out of every eight total layers.” - from [24]
The most interesting of the DBRX launch competitors is Jamba [24], an open (Apache 2.0 license) model (download it here) based upon a state space model (SSM), called Mamba, that has recently shown promise in the language modeling domain. Jamba is an SSM-transformer model that is the first production-scale variant of Mamba, derived by combining SSMs with key components of the transformer architecture. In particular, Jamba is composed of MoE layers, as well as selected parts from Mamba and the transformer; see below. MoE layers are used to add extra capacity to the model, and authors in [24] mention that number of experts is tuned to maximize quality/throughput on a single 80GB GPU.
The model has a 256K context window and can even fit 140K tokens of context on a single GPU! Compared to LLMs like Mixtral, Jamba has 3× faster inference due to the ability of SSMs (like Mamba) to address key limitations of the vanilla transformer architecture, such as:
Larger memory footprint with long contexts.
Slow inference with long contexts (self-attention cost grows quadratically).
Typically, the downside of Mamba is that it does not match the quality of top LLMs due to not performing attention over the entire context. However, the performance of Jamba is actually quite impressive, as shown below.
RAFT: Adapting Language Model to Domain Specific RAG [1]
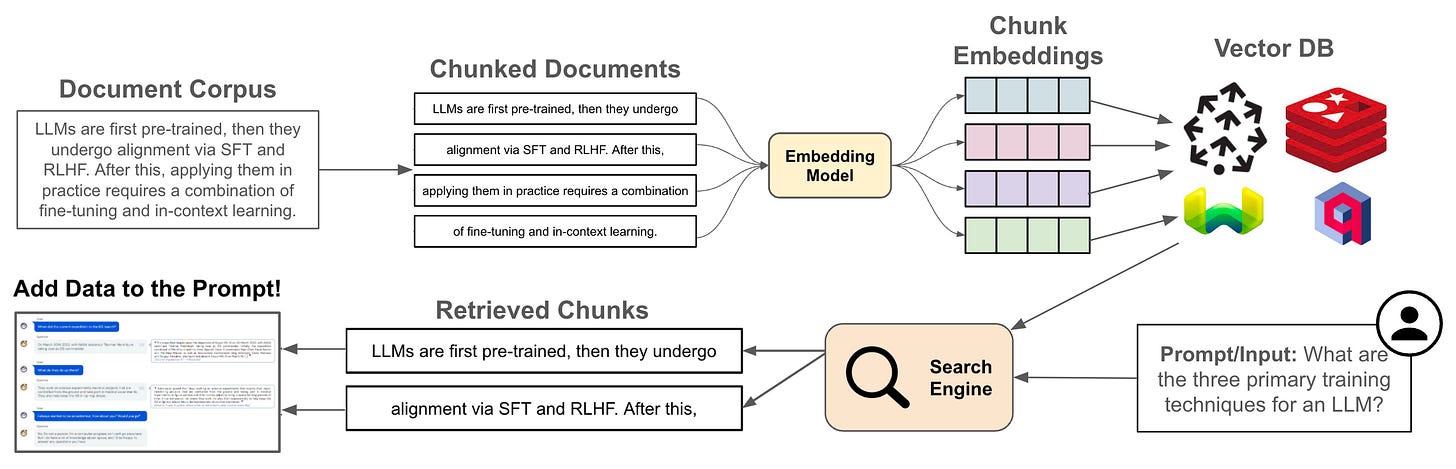
Most use cases with LLMs require specializing the model to understand new information that was not present during pretraining or finetuning. For example, we might have a set of company documents about which we want the model to answer questions. What is the best way to bake this knowledge into our LLM? This question has been studied a lot recently, spurring the creation of a research topic referred to as knowledge injection. Within this line of research, we have seen that retrieval augmented generation (RAG) is an effective approach [2], but authors in [1] extend this technique by proposing retrieval augmented finetuning (RAFT)—a finetuning recipe for making LLMs better at RAG.
Different QA setups. When performing RAG, we assume access to information that can be used by the LLM to better answer a question; see above. However, there are a few different problem setups that are commonly considered for performing question answering with an LLM:
Closed book: use the LLM as a chatbot and rely upon its internal (parametric) knowledge to answer the question properly.
Open book: allow the LLM to refer to external sources of information5 when answering the question.
In [1], we study a modification of the open book setup called domain-specific open book question answering. This setup assumes that we have both i) an open book setup and ii) prior knowledge of the domain in which the LLM will be tested. By having access to relevant, domain-specific information ahead of time, we can finetune the model on this data to aid the knowledge injection process.
For example, if we want to build an LLM to answer questions based on a fixed set of internal company documents, we can finetune our model on these documents prior to performing any question answering. As we will see, RAFT is just a particular finetuning strategy that is proposed for domain-specific open book question answering tasks. This finetuning strategy focuses upon improving the LLM’s ability to perform RAG, thus boosting the quality of knowledge injection.

What is RAFT? The first step in performing RAFT is to construct a training dataset. Each data example in this training dataset has three components:
A question that the LLM is expected to answer.
A set of documents that the LLM can use to help answer the question.
A chain-of-thought (CoT)-style [3] answer generated from one of the documents.
Using these components, we can use a prompt template to construct training examples with the structure shown below. Here, we should notice that portions of the response that are directly sampled from a document are surrounded by the special ##begin_quote## and ##end_quote## tokens, which allow the model to learn to rely upon document context when producing an answer.
We can then finetune the LLM—using supervised finetuning (SFT)—on such data to produce answers from the provided documents. When creating training examples for RAFT, we use CoT-style responses (i.e., these are usually generated with the help of GPT-4) in particular to hone the model’s reasoning capabilities. The model learns to output CoT-style answers based upon the question and provided context. This finetuning process is the core of the RAFT approach.
Document types. Although each training example in RAFT contains a set of documents, we can further classify these documents as one of two types:
Oracle documents: the answer to the question can be reasonably deduced from these documents.
Distractor documents: these documents do not contain useful (answer-related) information.
During training with RAFT, we set a hyperparameter P, such that P% of questions in the dataset have both oracle and discriminator documents included within the training example. For 1-P% of the documents, we only use distractor documents and remove the oracle document. By doing this, RAFT trains the model to disregard documents that have no useful information for crafting a response.
“By removing the oracle documents in some instances of the training data, we are compelling the model to memorize domain-knowledge.” - from [1]
Additionally, excluding relevant documents also forces the LLM to learn new, domain-specific information during finetuning to a certain extent. See below for a depiction of the RAFT pipeline and its comparison to standard RAG.
The RAFT approach is very similar to finetuning strategies proposed for teaching LLMs to make valid API calls; e.g., Gorilla [4] or RAT. However, RAFT generalizes these approaches beyond just API calls, focusing on making the model generally better at using any form of context for RAG applications.
Empirical evaluation. In [1], authors finetune a LLaMA-2-7B model using the RAFT approach. When evaluating this model, we see that it becomes much better at performing RAG on the documents upon which it is trained; see below.
Although these results are exactly what we would expect, they truly demonstrate the benefit of RAFT for domain-specific open book question answering. Namely, if we have access to the documents about which we want an LLM to answer questions ahead of time, then we can finetune the LLM over these documents (using RAFT) to significantly improve the quality of RAG!
Language models scale reliably with over-training and on downstream tasks [5]
“We fit scaling laws that extrapolate in both the number of model parameters and the ratio of training tokens to parameters.” - from [5]
Prior work has discovered scaling laws [6, 7] for language models, which show that model performance improves as we i) make the model larger and ii) increase the amount of data over which the model is pretrained. However, there are two main limitations of this work that make scaling laws less practical:
These works always study the compute-optimal regime [6], but language models are rarely trained in a compute-optimal manner in practice. Usually, we train smaller models over a larger number of tokens (i.e., overtraining) relative to the compute-optimal approach6 because smaller models are cheaper to use at inference time.
Performance is measured in terms of next-token prediction loss when measuring scaling laws, but performance on downstream tasks is what actually matters in most applications.
With this in mind, we might wonder: Do scaling laws still hold for more practical settings? In [5], authors aim to answer this question by training language models with sizes ranging from 0.011B to 6.9B parameters over a variable number of tokens samples from RebPajama, C4, or RefinedWeb. From these models, we can measure scaling laws for overtrained models, as well as study the correlation between model loss and aggregate performance on downstream tasks.
What is a power law? To understand scaling laws, we first need to understand the concept of a power law. In its most basic form, a power law is expressed as shown in the equation above7. A power law simply tells us that two variables (x and y) have a relationship—changing x produces a scale-invariant change in y. The shape of this relationship is controlled by the values of constants λ and α. If we plot this power law (with settings λ = 1.0, α = 0.5, and 0 < x, y < 1) regularly and in log-log format, we get the graphs shown in the figure below.
The linear log-log plot shown above, which has a slope of -α and a y-intercept of log(λ), is the signature of a power law. For LLMs, the quantity y is typically the next-token prediction loss on a validation set, while x can be several different quantities of interest. For example, we can study the validation loss with respect to compute used during training, number of model parameters, or amount of pretraining data. By plotting the power laws with respect to each of these quantities, we get a familiar picture; see below. The model’s loss decreases smoothly—according to a power law—as each of these quantities are increased.
Why is this useful? As we know, training a language model is an expensive process. The benefit of power laws is that they can help us to mitigate this expense. Namely, we can
Train several smaller models.
Fit a power law to their performance.
Use this power law to extrapolate and predict the performance of larger (and more expensive) training runs.
Using this approach, we can predict the performance of our LLM in advance and determine the optimal training settings without wasting compute on tuning!
“To reduce the cost of finding successful training recipes, researchers first evaluate ideas with small experiments and then extrapolate … to larger scales.” - from [5]
If we can extrapolate LLM performance reliably, we can iterate quickly at smaller scales and select the best settings for large-scale training runs. In the literature, this strategy has been used to predict compute-optimal settings by solving the formulation shown below, which tells us the optimal model and dataset size to use for achieving the best possible test loss given a fixed compute budget.
Overtrained LLMs. Authors in [5] begin by generalizing the compute-optimal training regime to the overtrained regime, where we train smaller models on more tokens. Although this approach is not compute-optimal, it is often adopted in practice due to the simple fact that the compute-optimal training formulation shown above completely ignores the inference cost of the resulting LLM. In most cases, we will happily pay a larger training cost to reduce the size of the model—assuming the model still achieves competitive performance—that we have to deploy.
“While loss should be higher than in the compute-optimal allocation for a given training budget, the resulting models have fewer parameters and thus are cheaper at inference.” - from [5]
To study overtraining, we can first introduce a ratio called the token multiplier that can be computed as M = D / N. Compute-optimal settings typically have a token multiplier of M ≈ 20. Exploring the overtraining regime, we see in [5] that scaling laws hold for different values of M ranging from 20 to 640; see below.
From this analysis, we learn that overtrained models obey similar power laws as those trained in a compute-optimal manner. Going further, we see in [5] that the value of M does not change the slope of the power law! Rather, only the y-intercept is changed, creating the group of parallel lines shown in the figure above. From these scaling laws, we can easily predict the performance of larger, overtrained models. For example, authors in [5] predict the validation loss of 1.4B and 6.9B parameter LLMs trained on 900B and 138B tokens, respectively, from a group of smaller-scale experiments that use 300× less compute.
Downstream performance. Taking the same group of LLMs used to discover scaling laws based upon the validation loss, we can plot their average top-1 error over a set of downstream evaluation tasks8. When the authors in [5] create these plots, they see that top-1 error in downstream tasks exponentially decays with respect to the model’s validation loss on the C4 dataset; see below.
This analysis reveals a clear trend in downstream task performance that authors in [5] use to propose a scaling law for top-1 error. Although the relationship between validation loss and top-1 error is dataset-dependent, we can fit a function to predict top-1 error as a function of compute and the amount of over-training. In [5], this strategy is used to predict the average top-1 error over downstream tasks for 1.4B and 6.9B parameter LLMs using 20× less compute.
Empirical evaluation. The first step of experiments in [5] is to train smaller LLMs with different values of M. We can then use scaling laws to extrapolate model performance to larger values of N and M. The main results of these experiments are shown in the figure above, where we see that the performance of larger-scale training runs—in terms of both validation loss and top-1 error on downstream tasks—can be reliably predicted using the scaling laws outlined in [5]. In particular, we see 0.7% relative error in predicting validation loss and 3.6% relative error in predicting top-1 error. As such, we clearly see in [5] that scaling laws are useful for predicting the performance of large-scale training runs in practice.
RewardBench: Evaluating Reward Models for Language Modeling [8]
Reinforcement learning from human feedback (RLHF) is almost universally used to power the LLM alignment process. Through alignment, practitioners can instill a variety of capabilities within an LLM; e.g., instruction following, steerability, safety, etc. One key component of RLHF is the reward model (RM), a copy of the original LLM that has been finetuned to predict whether a human user will prefer one piece of text over another. Despite the key role of RMs in RLHF, however, RMs—and the entire RLHF process in general!—are rarely documented and poorly analyzed within the AI research community. Many types of RMs and training strategies exist, which makes best practices for training effective RMs that yield good downstream results with RLHF unclear.
“Reward models (RMs) are at the crux of successful RLHF to align pretrained models to human preferences, yet there has been relatively little study that focuses on evaluation of those reward models.” - from [8]
To mitigate these issues, authors in [8] propose RewardBench—a common framework for comprehensively evaluating many different types of RMs. The goal of RewardBench is to create an open benchmark (i.e., meaning that all data and evaluation code is released) that can be used to granularly chart the landscape of 50+ RMs that are publicly available—authors in [8] even create a public leaderboard to fulfill this purpose. This benchmark is an easily-extendable piece of infrastructure that can be expanded to new RMs and datasets that are proposed over time.
RewardBench, which includes new evaluation datasets across several categories of RM performance, is the most comprehensive evaluation suite yet created for RMs9, and it can be easily extended to include new evaluation suites or custom sources of data. By studying the performance of RMs on RewardBench, we can better understand why RMs work. RewardBench aims to create a common framework that allows us to evaluate RMs in a structured manner across many capabilities that might be created during alignment.
What is RLHF? Oftentimes, the goal of LLM alignment is difficult to concretely define. Instead, we usually construct a set of alignment criteria (e.g., helpfulness, safety, steerability, instruction following, etc.) that can be used to characterize a high-quality response from an LLM. Following this strategy, the first step of the RLHF process (depicted above) is constructing a preference dataset. Each example in this dataset contains a prompt and at least two responses, where the responses are ranked by a human annotator according to their quality. In most cases, we assume that each prompt has two responses, and the human annotator simply identifies the “better” response according to the alignment criteria.
“The prevalence of RLHF stems from its efficacy at circumventing one of the greatest difficulties in integrating human values and preferences into language models: specifying an explicit reward” - from [8]
From the preference data, we can train an RM to identify whether a human user will prefer one piece of text over another. Then, we can use a reinforcement learning (RL) algorithm like PPO to finetune the LLM according to the signal from the RM. This process finetunes the LLM to produce outputs that are more preferable to humans, as measured by the RM. In this way, we can instill the alignment criteria into the LLM without explicitly specifying a reward function, which is the core characteristic that underlies the popularity of RLHF. For more details on RL and how it can be used to finetune an LLM, check out the articles below:
Basics of Reinforcement Learning for LLMs [link]
Policy Gradients: The Foundation of RLHF [link]
Proximal Policy Optimization (PPO) [link]
RLHF variants. In the typical setup, an RM outputs a single, scalar value that captures the human preference score for an LLM’s output. The architecture of the RM is identical to the original LLM, but we append a linear layer to the end of this model that predicts a single value (or logit). As formulated in the figure below, the RM in most cases is trained using a classification objective to predict human preference probabilities according to the Bradley-Terry model [10].
However, there are also popular alternatives to RLHF, such as Direct Preference Optimization (DPO) [11] that use different RM structures. In the case of DPO, we completely eliminate the need for a separate reward model during alignment. Instead, an implicit reward is constructed using probabilities of the model being trained, as well as probabilities of the base model. Such an approach has gained in popularity recently due to its simplicity and lower compute footprint. However, the DPO models and the difference between DPO and classifier-based RMs has not been extensively analyzed—an issue that authors in [8] aim to solve.
RewardBench design. The RewardBench dataset is comprised of prompts paired with two responses—one good and one bad. To evaluate an RM, we can simply test whether it is capable of identifying the preferred response. This ability to correctly identify the preferred response can be easily captured via an accuracy metric, as shown within the figure above. Then, we can compare different RMs by seeing where they agree or disagree across this dataset. To study RMs on a more granular level, authors also create difficult preference examples that have subtle, but verifiable, reasons why one response should be preferred to another. Ideally, the RM should capture these subtle differences and assign credit to the preferable response in a stable manner. To ensure that length bias [12] does not skew results, authors ensure that all response pairs within RewardBench are of similar length.
Evaluation subsets. As previously mentioned, RewardBench aims to capture RM performance across all relevant categories. For this reason, five different subsets are created for evaluating different capabilities:
Chat: tests the RM’s ability to distinguish correct chat responses; data is selected from AlpacaEval and MT Bench.
Chat Hard: tests the RM’s ability to identify trick questions and subtle differences between responses; data selected from response pairs with similar ratings on MT Bench and adversarial data taken from LLMBar.
Safety: tests refusals of dangerous prompts and ability to avoid incorrect refusals (even with similar trigger words); data selected from XSTest, Do-Not-Answer, and an internal dataset from AI2.
Reasoning: tests coding and reasoning abilities; data selected from HumanEvalPack10 and PRM800K.
Prior datasets: existing preference datasets (e.g., Anthropic’s HH dataset, Stanford Human Preferences dataset, and OpenAI’s learning to summarize dataset) are also aggregated and added into their own category of RewardBench to encourage consistency with prior work.
Within each category of RewardBench, models are evaluated in terms of their accuracy. To generate an aggregate score per category, we take a weighted average of examples within that category. For example, the chat subset takes a weighted average of accuracy on AlpacaEval and MT Bench based on the size of each dataset, while the reasoning category weights coding and reasoning subsets equally. To get a top-level score on RewardBench, we just take a uniform average of accuracy across all of the different data subsets.
Analysis of RMs. The empirical results from [8] are outlined above. The empirical analysis of [8] is extensive, and I would recommend reading the paper for all of the details. However, the high-level takeaways of this analysis can be summarized as follows:
The performance of 50+ different RMs with sizes ranging from 300M to 70B parameters is measured, and results are grouped into categories based on the size of the RM (i.e., small, medium or large).
Only large RMs perform well consistently on the more difficult Chat Hard and Reasoning subsets of RewardBench. Most RMs struggle with the Chat Hard and Reasoning subsets, revealing an area of improvement for RMs.
We see a clear, monotonic performance improvement as DPO models become larger, but this trend is less clear for classifier-based RMs—there are striations in performance that resemble standard LLM evaluations.
Results on prior evaluation datasets are not entirely consistent with RewardBench. For example, DPO models consistently perform well on RewardBench but struggle on legacy benchmarks.
RMs have various training strategies that result in different distributions and magnitudes of rewards assigned by each RM (see below). The research community has yet to select a standard output distribution for RMs that results in the best downstream performance with RLHF.
Work in [8] is just the start of an entire movement—largely pioneered by Nathan Lambert at AI2—for democratizing understanding of LLM alignment and RLHF. In fact, Nathan has already began partnering with proprietary LLM providers like Cohere—see here for a discussion—to benchmark their RMs on RewardBench and provide more transparency into the alignment process.
Simple and Scalable Strategies to Continually Pre-train Large Language Models [13]
As shown in the figure above, the first step of the LLM training pipeline is to pretrain the randomly-initialized model over a massive corpus of raw text. However, there are two key limitations of this approach:
Pretraining is very expensive.
Training data is constantly evolving/expanding in the real world.
Ideally, we would want the ability to easily train or adapt the LLM to understand fresh data as it becomes available, but frequently re-running the pretraining process is cost prohibitive. Such a dilemma has caused the topic of knowledge injection, which refers to the process of teaching an LLM new or domain-specific knowledge, to become popular in recent research.
“Our results demonstrate that LLMs can be successfully updated via simple and scalable continual learning strategies, matching the re-training baseline using only a fraction of the compute.” - from [13]
In prior work [14], we have seen that retrieval-based approaches for knowledge injection—retrieval-augmented generation (RAG) in particular—are effective in practice and outperform continued pretraining (or finetuning) handily in most cases. In [13], however, authors focus on the continued pretraining regime and show that these findings are less applicable in settings where we are adapting the LLM to larger amounts (i.e., several hundred billion tokens) of incoming data. In these cases, continued pretraining is surprisingly effective when tuned properly.
Continual pretraining. Authors in [13] propose a particular training setup, called continual pretraining (see above), in which we have a sequence of N datasets, where N >= 2 and each dataset is no smaller than 100B tokens. There may be large distribution shifts (e.g., the introduction of a new language or skill) between each of these datasets, and our goal is to learn from these datasets in sequence. One popular training strategy that follows this structure is continued pretraining of a publicly-available base model (e.g., LLaMA-2) on domain-specific data.
The naive approach. Given the continual pretraining setup described above, we might wonder how we can incorporate a new, large corpus of data into an LLM. Immediately, there are two naive approaches that we might consider:
Combine this data with the original pretraining set and re-run the pretraining process (from scratch) over the full dataset.
Finetune the LLM over this data using a continued pretraining approach.
Unfortunately, these approaches have limitations: i) pretraining is expensive and cannot be performed frequently, ii) the model might not adapt well to the new dataset, and iii) finetuning (or continued pretraining) on the new data in isolation may lead to catastrophic forgetting11. To get around these issues, we need a simple and scalable continual learning strategy that does not deteriorate the LLM’s understanding of prior data—this is exactly the core contribution of [13].
Training strategies. To study continual pretraining, authors in [13] derive two different training setups12:
Continual pretraining: given an LLM that has been pretrained on
D1, we further pretrain the model onD2.Combined pretraining: we combine datasets
D1andD2together, then pretrain a randomly-initialized model on the full data.
Of the two approaches outlined above, we know that combined pretraining will work well. However, this approach is expensive, as we must pretrain the LLM from scratch each time we want to incorporate new data. Simply continuing the pretraining process over the new data would be much easier and more dynamic, but this approach could also lead to catastrophic forgetting if handled incorrectly.
A practical strategy for continual pretraining. In [13], authors discover that—given a few additional tricks—we can achieve impressive performance with continual pretraining, even matching or exceeding the performance of combined pretraining! The key details for performing effective continual pretraining, which are outlined in the figure above, are twofold:
We must perform a linear warmup and cosine decay of the learning rate during continued pretraining, just as is done during pretraining.
We must add a small amount of the previous data into the continual pretraining process to avoid catastrophic forgetting (i.e., similar to using a replay buffer in continual learning).
“We demonstrate, across two model sizes and distribution shifts, that a simple and scalable combination of LR re-warming, LR re-decaying, and compute-equivalent replay allows continually pre-trained models to attain similar performance to models re-trained on the union of all data while using significantly less compute.” - from [13]
When we adopt these simple tricks, LLMs perform surprisingly well in the continual pretraining setting; see below. Plus, authors in [13] even show that this approach is robust to relatively large domain shifts; e.g., learning a new language.
Brief personal note. I am especially fond of this paper because I studied similar topics during my PhD. My findings, documented in this paper, were that we can develop practical (and surprisingly effective) methods for continual training of neural networks by just storing previous data in a replay buffer and sampling data from this buffer throughout the training process. This approach, although very simple, yields impressive results—even exceeding the performance of models trained using standard training strategies—if we are sure to tune the hyperparameters properly. As we see in [13], such a strategy generalizes almost perfectly to LLMs!
Sequoia: Scalable, Robust, and Hardware-aware Speculative Decoding [17]
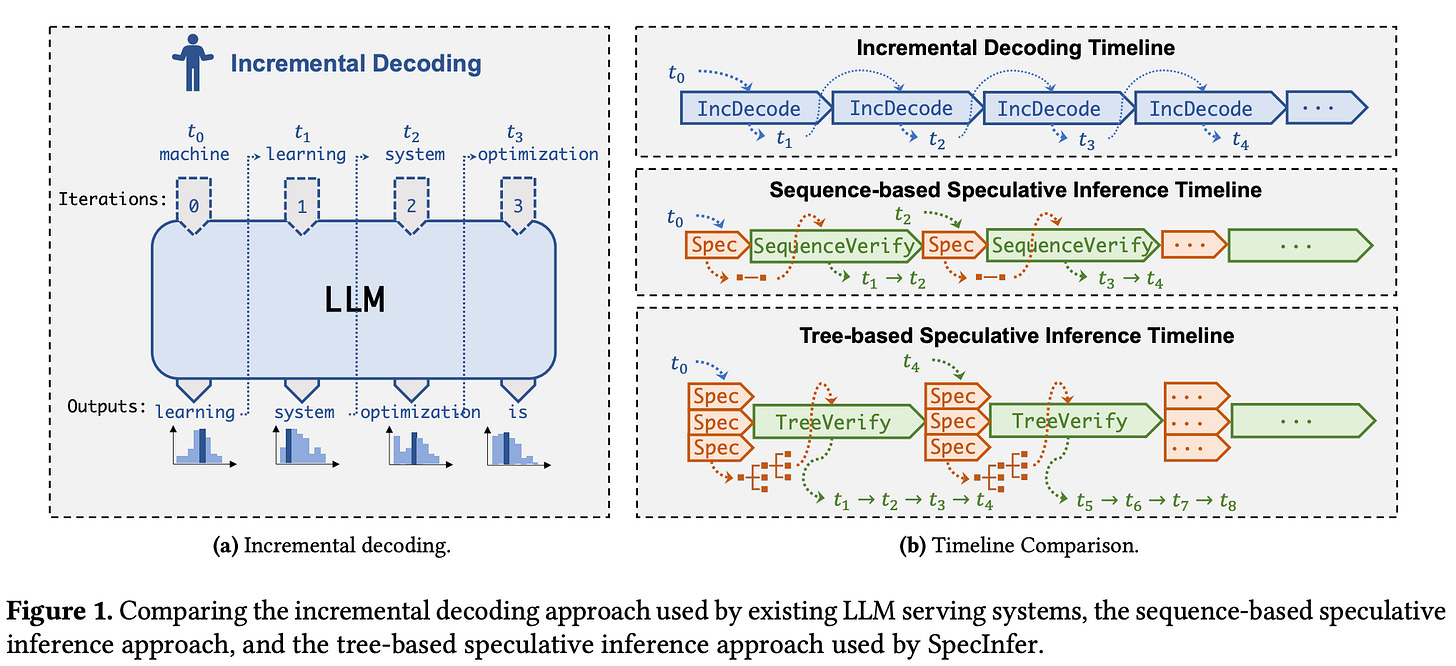
Despite the rapid adoption of LLMs, efficiently serving these models is difficult. LLMs generate tokens using an autoregressive next token prediction process; see below. This process generates a single token at a time, but generating this token requires the use of all model parameters, which creates an IO bottleneck and causes hardware to be poorly utilized during inference/decoding. Authors in [17] propose a hardware-aware speculative decoding strategy, called Sequoia, that mitigates these issues. Sequoia can serve LLMs efficiently on consumer GPUs, increases decoding speed up to 10X (see above13), and maintains the original output distribution of the LLM (i.e., no approximations are made).
What is speculative decoding? Speculative decoding is a widely-used technique for speeding up the inference process of an LLM without changing its output distribution. To do this, we create one or more smaller “draft” models that can predict (or “speculate”) output tokens that the LLM will produce. The predictions of draft model(s) can then be organized into a tree structure, where nodes within the tree represent sequences of speculated tokens; see below. The correctness of the speculations are then verified in parallel through a single forward pass of the actual LLM. By storing speculated tokens in a tree (i.e., as opposed to a sequence) we can increase the number of tokens accepted by the LLM during verification by providing several options for each token position instead of a single option.
In the figure above, we see a comparison of incremental decoding (i.e., the vanilla, autoregressive token generation process for LLMs) to both sequence and tree-based speculative decoding. Although tree-based speculative decoding yields improved inference throughput in many cases, there are still issues with existing techniques! For example, algorithms like SpecInfer [18] and Spectr [19] are sub-optimal for larger token trees, are sensitive to inference hyperparameter (e.g., temperature), and cannot optimize the size and shape of the speculated tree based upon the available hardware configuration. With this in mind, authors in [17] aim to answer the following question: “How can we design an optimal tree-based speculative decoding method to maximize speedups on modern hardware?”
Sequoia [17], as depicted within the figure above, can obtain up to 10× speedups compared to incremental decoding strategies. To obtain these speedups, authors in [17] make three key contributions:
Optimize the tree structure: In Sequoia, tree construction is formulated as a constrained optimization problem14, and a dynamic programming (DP) approach is used to discover the optimal speculative token tree.
Avoiding the same mistakes: Sequoia samples tokens without replacement from the draft model, which i) prevents the draft model from making the same mistake twice and ii) still maintains the LLM’s output distribution.
Considering the hardware: Sequoia uses a hardware-aware tree optimizer, where verification time is a hardware dependent function of the number of tokens being verified, to solve for the optimal tree shape and depth.
At a high level, Sequoia [17] goes beyond prior work by considering the impact of hardware configuration on verification time and investing heavily into finding an optimal tree structure. The result is a hardware-aware speculative decoding framework that can drastically improve the efficiency of serving large LLMs, even on consumer GPUs (e.g., Nvidia RTX-4090 or 2080Ti). When implemented on top of HuggingFace / Accelerate, the results of Sequoia are impressive; see below.
“We can serve a Llama2-70B on a single RTX-4090 with an average time between tokens (TBT) as low as 0.57s, which is 8X faster than a highly optimized offloading serving system, 9X faster than DeepSpeed-Zero Offloading. On a single 2080Ti GPU (only 11GB memory), Vicuna-33B can be served with a TBT of 0.87s.” - from [17]
DenseFormer: Enhancing Information Flow in Transformers via Depth Weighted Averaging [20]
The transformer architecture is used almost universally across domains, but researchers are still making fundamental improvements to this architecture. In [20], a simple modification is proposed that provides—at each layer of the transformer—direct access to the output of prior layers. In particular, we take a weighted average of all prior layers’ output representations after each transformer block, and the weights used in this average are learned during training; see above. This operation, called a Depth Weighted Average (DWA), is used to create the DenseFormer architecture in [20], which requires fewer layers to perform well and has better data efficiency, a lower memory footprint, and faster inference times compared to the vanilla transformer model.
Making it efficient. Added DWA operations in the DenseFormer have minimal memory15 and compute overhead. However, the DWA operation is IO intensive, as we must consider all prior layers’ output representations when computing the current layer’s output. To solve this, authors in [20] add dilation and periodicity to DWA. At a high level, this means that we modify DWA to sparsely consider prior layers’ outputs (i.e., instead of always considering all prior outputs). When depicting the weights of DWA as a matrix (shown above), dilation and periodicity just sparsify the row and column entries of this matrix, respectively, ensuring that each layer of the DenseFormer only considers a subset of prior layer outputs in DWA. By adding sparsity to DWA, the DenseFormer achieves the same perplexity gains while matching the speed of the vanilla transformer model.
Why does this work well? To understand the inner workings of the DenseFormer, authors investigate patterns within the learned DWA weights. As shown in the figure above, there are three visible patterns that emerge in the weights of DWA:
Diagonal entries always have high weights, indicating that we consider the current layer’s output heavily relative to prior layers.
The first column of the matrix is weighted heavily, indicating that the DenseFormer assigns high weights to the model’s initial embedding vectors.
A block of high weights exists near the final layer, which seems to perform an aggregation over outputs of the last several layers.
Overall, adding DWA operations into the transformer allows the model to more easily re-use features from earlier layers without propagating them through many layers—there is a direct path from early layers to later layers. This property seems to improve data efficiency and heighten the model’s accuracy in general.
Performance and implementation. With direct access to all previous blocks’ outputs (i.e., no sparsity in DWA), the 48-block DenseFormer far outperforms the vanilla transformer model, but this performance comes at the cost of degraded inference and training speeds. As shown above, however, we can modify the dilation and periodicity to mitigate this issue, eventually achieving comparable improvements in performance without degrading the model’s speed. The DenseFormer can be implemented in only a few lines of code by using the Python package created by the authors of [20]. Despite its benefits, one notable criticism of the DenseFormer architecture is its lack of compatibility with pipeline parallelism—an important component of scaling training for LLMs.
Honorable Mentions
We covered a variety of papers and topics within this post, but research on LLMs is moving incredibly fast. New techniques and models are being proposed every day. Here are some other interesting, recent contributions that I’ve had my eye on:
“MM1: Methods, Analysis & Insights from Multimodal LLM Pre-training”: An extensive empirical writeup on training multimodal large language models (MLLMs) from Apple [link]
“Recurrent Drafter for Fast Speculative Decoding in Large Language Models”: Another speculative decoding algorithm that claims to improve inference efficiency for LLMs (also from Apple16) [link]
“Stealing Part of a Production Language Model”: This paper shows that you can exploit the logprobs returned from an LLM API to extract information about the model behind the API, such as the hidden dimension or even the entire token embedding projection layer [link]
“Training great LLMs entirely from ground up in the wilderness as a startup”: Very interesting blog post that details the process (and difficulties) of setting up necessary infrastructure from scratch for training LLMs at a startup [link]
“tinyBenchmarks: evaluating LLMs with fewer examples”: The evaluation process for LLMs is typically very expensive, but this paper explores cheaper methods for evaluating LLMs with similar reliability [link]
“Set the Clock: Temporal Alignment of Pretrained Language Models”: LLMs are trained on data from varying points in time, but this paper explores the alignment of an LLM’s internal knowledge to a certain point in time (i.e., “temporal alignment”) [link]
“A Survey on Data Selection for Language Models”: An extremely thorough survey of existing research on how to optimally construct pretraining datasets for LLMs [link]
New to the newsletter?
Hi! I’m Cameron R. Wolfe, and this is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews of relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on Medium, X, and LinkedIn!
Bibliography
[1] Zhang, Tianjun, et al. "RAFT: Adapting Language Model to Domain Specific RAG.” arXiv preprint arXiv:2403.10131 (2024).
[2] Ovadia, Oded, et al. "Fine-tuning or retrieval? comparing knowledge injection in llms." arXiv preprint arXiv:2312.05934 (2023).
[3] Wei, Jason, et al. "Chain of thought prompting elicits reasoning in large language models." arXiv preprint arXiv:2201.11903 (2022).
[4] Patil, Shishir G., et al. "Gorilla: Large Language Model Connected with Massive APIs." arXiv preprint arXiv:2305.15334 (2023).
[5] Gadre, Samir Yitzhak, et al. "Language models scale reliably with over-training and on downstream tasks." arXiv preprint arXiv:2403.08540 (2024).
[6] Hoffmann, Jordan, et al. "Training compute-optimal large language models." arXiv preprint arXiv:2203.15556 (2022).
[7] Kaplan, Jared, et al. "Scaling laws for neural language models." arXiv preprint arXiv:2001.08361 (2020).
[8] Lambert, Nathan, et al. "RewardBench: Evaluating Reward Models for Language Modeling." arXiv preprint arXiv:2403.13787 (2024).
[9] Stiennon, Nisan, et al. "Learning to summarize with human feedback." Advances in Neural Information Processing Systems 33 (2020): 3008-3021.
[10] Bradley, Ralph Allan, and Milton E. Terry. "Rank analysis of incomplete block designs: I. The method of paired comparisons." Biometrika 39.3/4 (1952): 324-345.
[11] Rafailov, Rafael, et al. "Direct preference optimization: Your language model is secretly a reward model." Advances in Neural Information Processing Systems 36 (2024).
[12] Prasann Singhal, Tanya Goyal, Jiacheng Xu, and Greg Durrett. A long way to go: Investigating length correlations in rlhf. arXiv preprint arXiv:2310.03716, 2023.
[13] Ibrahim, Adam, et al. "Simple and Scalable Strategies to Continually Pre-train Large Language Models." arXiv preprint arXiv:2403.08763 (2024).
[14] Ovadia, Oded, et al. "Fine-tuning or retrieval? comparing knowledge injection in llms." arXiv preprint arXiv:2312.05934 (2023).
[15] Ouyang, Long, et al. "Training language models to follow instructions with human feedback." Advances in neural information processing systems 35 (2022): 27730-27744.
[16] Glaese, Amelia, et al. "Improving alignment of dialogue agents via targeted human judgements." arXiv preprint arXiv:2209.14375 (2022).
[17] Chen, Zhuoming, et al. "Sequoia: Scalable, Robust, and Hardware-aware Speculative Decoding." arXiv preprint arXiv:2402.12374 (2024).
[18] Miao, Xupeng, et al. "Specinfer: Accelerating generative llm serving with speculative inference and token tree verification." arXiv preprint arXiv:2305.09781 (2023).
[19] Sun, Ziteng, et al. "Spectr: Fast speculative decoding via optimal transport." Advances in Neural Information Processing Systems 36 (2024).
[20] Pagliardini, Matteo, et al. "DenseFormer: Enhancing Information Flow in Transformers via Depth Weighted Averaging." arXiv preprint arXiv:2402.02622 (2024).
[21] “Introducing DBRX: A New State-of-the-Art Open LLM.” Databricks Mosaic AI Research, 27 March 2024, https://www.databricks.com/blog/introducing-dbrx-new-state-art-open-llm.
[22] Madaan, Aman, et al. "Language models of code are few-shot commonsense learners." arXiv preprint arXiv:2210.07128 (2022).
[23] Zoph, Barret, et al. "St-moe: Designing stable and transferable sparse expert models." arXiv preprint arXiv:2202.08906 (2022).
[24] “Introducing Jamba: AI21's Groundbreaking SSM-Transformer Model” AI21 Labs, 28 March 2024, https://www.ai21.com/blog/announcing-jamba.
[25] “Qwen1.5-MoE: Matching 7B Model Performance with 1/3 Activated Parameters”, Qwen, 28 March 2024, https://qwenlm.github.io/blog/qwen-moe/
This is a massive dataset! For reference, MPT-7B and MPT-30B were trained on 1T tokens of text.
The quality of datasets used to train DBRX are a result of the research by Cody Blakeney and the rest of the Data Research team at Mosaic. In fact, some members of this team have even branched off to form an entirely new startup that is 100% focused upon improving data quality.
According to researchers at Mosaic, the GPT-4 tokenizer was selected partly due to performance and partly due to the practical consideration that it makes pricing comparisons to competing models (i.e., GPT-4) more direct/simple.
This comes as no surprise because the model has strong coding abilities—likely because the pretraining data mixture contains a lot of code—and training on more code is known to yield improved reasoning capabilities in the LLM [22].
Usually, this information is surfaced via a retrieval mechanism. For example, RAG typically retrieves the K most relevant documents to include in the model’s prompt when answering a question.
For example, if the compute-optimal approach to achieve a given loss L is a 7B parameter model trained over 800B tokens, maybe we will instead train a 3.5B parameter model over 2T tokens to achieve the same loss L.
Here, we consider an inverse power law (i.e., p is negative) because scaling laws are always inverse for language models. The loss decreases with more compute.
In [5], authors use the evaluation gauntlet within Mosaic AI’s LLM foundry to compute downstream performance metrics.
Some analysis of RMs has been conducted, but it is usually done on datasets with known issues. For example, both Anthropic’s helpful and harmless dataset, as well as OpenAI’s learning to summarize dataset are commonly used to evaluate RMs despite being known to have high levels of inter-annotator disagreement.
Examples are created by pairing correct code from the existing dataset with code that is known to contain bugs.
“Catastrophic forgetting” is a common term in active/online learning research. Put simply, it refers to the phenomenon of a neural network completely forgetting about previously learned skills or data when being trained on new data.
In describing these setups, we assume that N = 2. However, we can adapt similar training strategies for N >= 3.
This video depicts the decoding/inference process (at 4X speed) of LLaMA-2-70B on a single RTX-4090 GPU both with and without Sequoia.
“In this optimization problem, we aim to maximize the expected number of tokens F(T ) generated by verifying a token tree T , under a constraint on the size of T .” - from [17]
The number of total added weights is d(d + 3) / 2, where d is the depth of the transformer. This number is negligible in comparison to the parameter count of modern transformer models (e.g., LLMs).
Apple seems to be publishing a lot of AI-related technical reports recently, indicating that they may be trying to heighten their reach and involvement within the AI research community.




























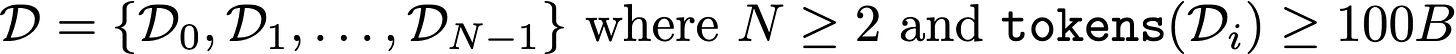








Hi Cameron, congratulations on these numbers, the academic depth and clarity with which they are written is impressive! I also write a paper-based newsletter, so that's even more inspirational!
I was curious: do you usually choose a topic first and then do research on the topic or is it usually a paper that inspires you and then you go accordingly?
how can you find and updata latest paper about all this is interesting, you have source or technique to do this, please suggest me, I'm new to this.