Policy Gradients: The Foundation of RLHF
Understanding policy optimization and how it is used in reinforcement learning...
This newsletter is presented by Rebuy, the commerce AI company.
If you like the newsletter, feel free to get in touch with me or follow me on Medium, X, and LinkedIn. I try my best to produce useful/informative content.
Although useful for a variety of applications, reinforcement learning (RL) is a key component of the alignment process for large language models (LLMs) due to its use in reinforcement learning from human feedback (RLHF). Unfortunately, RL is less widely understood within the AI community. Namely, many practitioners (including myself) are more familiar with supervised learning techniques, which creates an implicit bias against using RL despite its massive utility. Within this series of overviews, our goal is to mitigate this bias via a comprehensive survey of RL that starts with basic ideas and moves towards modern algorithms like proximal policy optimization (PPO) [7] that are heavily used for RLHF.
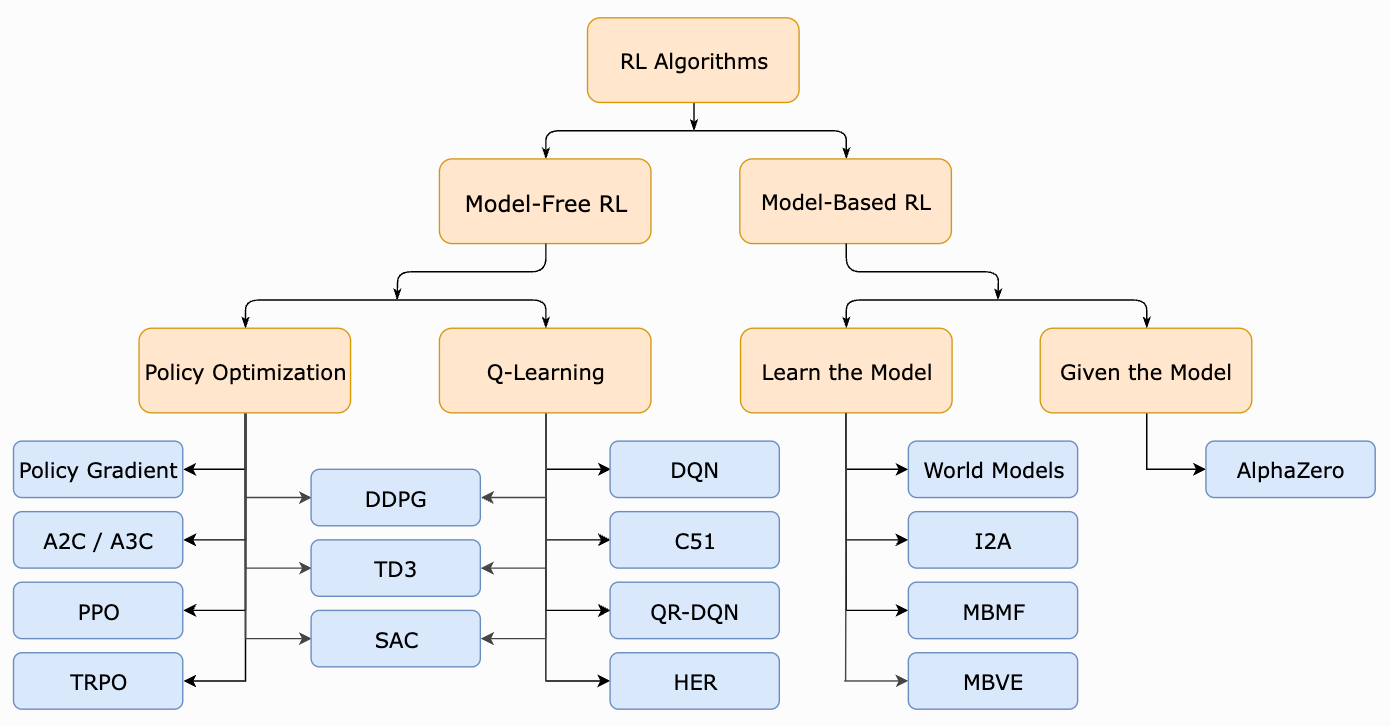
This overview. As shown above, there are two types of model-free RL algorithms: Q-Learning and Policy Optimization. Previously, we learned about Q-Learning, the basics of RL, and how these ideas can be generalized to language model finetuning. Within this overview, we will overview policy optimization and policy gradients, two ideas that are heavily utilized by modern RL algorithms. Here, we will focus on the core ideas behind policy optimization and deriving a policy gradient, as well as cover a few common variants of these ideas. Notably, PPO [7]—the most commonly-used RL algorithm for finetuning LLMs—is a policy optimization technique, making policy optimization a fundamentally important concept for finetuning LLMs with RL.
Reinforcement Learning Basics
“In a nutshell, RL is the study of agents and how they learn by trial and error. It formalizes the idea that rewarding or punishing an agent for its behavior makes it more likely to repeat or forego that behavior in the future.” - from [5]
In a prior overview (linked below), we learned about the problem structure that is typically used for reinforcement learning (RL) and how this structure can be generalized to the setting of fine-tuning a language model.
Understanding these fundamental ideas is important, as it lays a foundation for more complex RL algorithms. Here, we will briefly overview these key ideas and introduce some extra concepts that are related to policy optimization.
MDPs and Fundamental Components in RL
The RL framework can be formalized as a Markov Decision Process (MDP), which has states, actions, rewards, transitions, and a policy; see below.
For the purposes of this post, we will assume that our policy is a machine learning model (e.g., a deep neural network) with parameters θ. This policy takes a state as input and predicts some distribution over the action space. We use this output to decide what action should be taken next within the MDP; see below.
By using our policy to predict each next action, we can traverse an environment, receive rewards, and form a sequential trajectory of states and actions. Typically, we refer to the entity traversing the environment as an agent, and our agent implements the policy shown above when choosing each action. The process of exploring an environment according to some policy is shown below.
Reward and return. As our agent traverses the environment, it receives positive or negative reward signals for the actions it chooses and the states that it visits. Our goal is to learn a policy from these reward signals that maximizes total reward across an entire trajectory sampled from the policy. This idea is captured by the return, which sums the total rewards over an agent’s trajectory; see below.
Here, the return is formulated with a discount factor. However, this discount factor is not always present or necessary. The two major types of returns considered within RL are the infinite-horizon discounted reward and the finite-horizon undiscounted reward; see below. For the infinite-horizon variant, the discount factor is necessary mathematically to ensure that the infinite sum converges; see here for more discussion on the role of the discount factor.
Value and Advantage Functions
One final concept that will be especially relevant to this post is that of a value function. In RL, there are four basic value functions (shown above), all of which assume the infinite-horizon discounted return:
On-Policy Value Function: expected return if you start in state
sand act according to policy π afterwards.On-Policy Action-Value Function: expected return if you start in state
s, take some actiona(may not come from the current policy), and act according to policy π afterwards.Optimal Value Function: expected return if you start in state
sand always act according to the optimal policy afterwards.Optimal Action-Value Function: expected return if you start in state
s, take some actiona(may not come from the current policy), and act according to the optimal policy afterwards.
There is an important connection between the optimal policy in an environment and the optimal action-value function. Namely, the optimal policy selects the action in state s that maximizes the value of the optimal action-value function.
Advantage functions. Using the value functions described above, we can define a special type of function called an advantage function, which is heavily used in RL algorithms based on policy gradients. Put simply, the advantage function characterizes how much better it is to take a certain action a relative to a randomly-selected action in state s given a policy π ; see above. Here, we should notice that the advantage function can be derived using the on-policy value and action-value functions defined before, as these functions assume that the agent acts according to a randomly-selected action from the policy π .
“The value of your starting point is the reward you expect to get from being there, plus the value of wherever you land next.” - from [5]
Connection to Bellman equations. Finally, we should note that each of the value functions have their own Bellman equation that quantifies the value of a particular state or state-action pair in RL. Bellman equations are the foundation of RL algorithms such as Q-Learning and Deep Q-Learning. See here for more details on how the Bellman Equation for each value function can be derived.
Policy Optimization
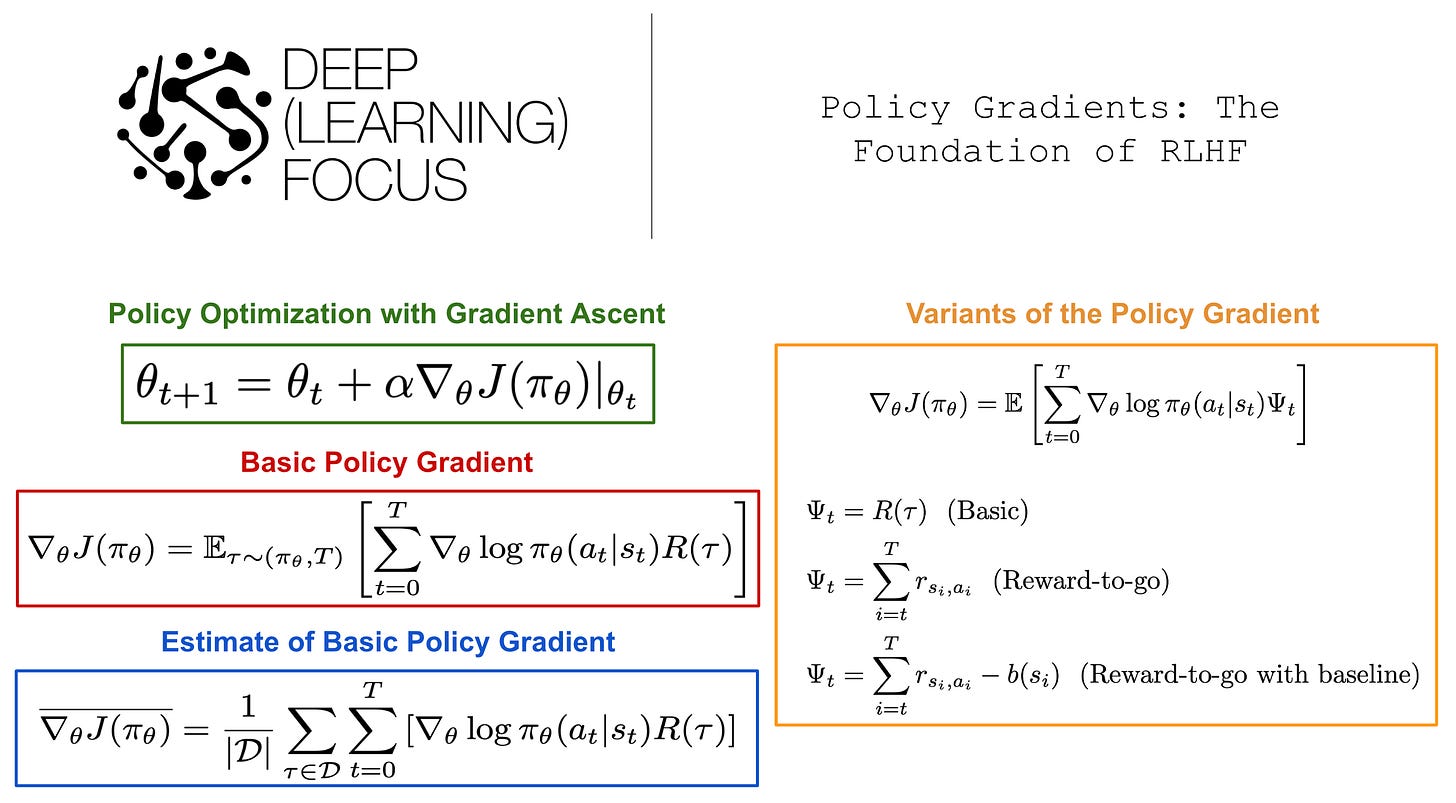
We will now explore the basic idea behind policy optimization, how this idea can be used to derive a policy gradient, and several variants of the policy gradient that commonly appear within RL literature. During the learning process, we aim to find parameters θ for our policy that maximize the objective function below.
In words, this objective function measures the expected return of trajectories sampled from our policy within the specified environment1. If we want to find parameters θ that maximize this objective function, one of the most fundamental techniques that we can use is gradient ascent, which iterates over parameters θ using the update rule shown below.
Gradient ascent/descent is a fundamental optimization algorithm that—along with its many variants—is heavily used for training machine learning models across a variety of different applications. See here for a more comprehensive survey of gradient descent/ascent in ML and the popular variants that exist. At each step of gradient ascent/descent, the above update rule executes the following steps:
Compute the gradient of the objective with respect to the current parameters.
Multiply this gradient by the learning rate.
Tweak the parameters by the addition/subtraction2 of this scaled gradient.
If we select the correct learning rate and perform sufficient iterations of this gradient ascent update, our policy should begin to increase the desired objective—this is the fundamental idea behind policy optimization. However, the number of required updates to reach convergence and whether we global or locally maximize the objective (if at all) depends upon the properties of the objective function. Though we will not cover the details here, there is an entire field of research, called optimization, that focuses upon mathematically analyzing the convergence of such (gradient-based) algorithms3 for optimizing objective functions.
Deriving (and using) a Basic Policy Gradient
If we want to implement the basic idea of policy optimization outlined above, the first question we might ask is: How do we compute the gradient of our objective? To answer this question, we need a bit of math. We will outline the basic ideas for how to do this here, but we will not go too in depth, choosing instead to focus on practical takeaways and resulting algorithms. If you’re not interested in math, skip to the bottom of this section and pay attention to the final expression that we derive for the policy gradient (highlighted clearly).
To start, let’s use the definition of the expected value in statistics to “unroll” the gradient of our objective.
What we see here is that the gradient of our objective relies upon the expected value of the return for our current policy. We can compute this expected return similarly to computing any other average value. Put simply, we consider all possible trajectories from our policy, compute their probability, multiply the return of each trajectory by its probability, and sum all of this together; see below.
Because our policy can have a potentially infinite number of trajectories, we have to express this operation as an integral instead of a discrete sum over trajectories. However, we see here that integrals are not super difficult to understand—they are just a different way of computing an average over a potentially infinite number of values!
From here, we should notice that this expression depends upon two quantities: the return of a trajectory and the probability of a trajectory under our current policy. Computing the return is easy—we just get this from our environment. We can compute the probability of a trajectory under the current policy as shown below.
Here, we use the chain rule of probability to derive the probability of the overall trajectory under the current policy by just multiplying the probability of each state and action in the trajectory. Then, by combining the expressions we have derived so far and applying the log-derivative trick, we arrive at the expression shown below; see here for a full derivation.
Now, we have an actual expression for the gradient of our objective function that we can use in gradient ascent! Plus, this expression only depends on the return of a trajectory and the gradient of the log probability of an action given our current state. As long as we instantiate our policy such that the gradient of action probabilities is computable (e.g., this is pretty easy to do if our policy is implemented as a neural network), we can easily derive both of these quantities!
Computing the policy gradient in practice. Computing the expectation used in the expression above analytically would require an integral. In practice, however, we can estimate the value of this expectation by sampling a fixed number of trajectories. In other words, we can just:
Sample several trajectories by letting the agent interact with the environment according to the current policy.
Estimate the policy gradient using an average of relevant quantities over the fixed number of sample trajectories.
See below for a formal expression of this idea, where we sample several trajectories and use their sample mean as an estimate of the policy gradient.
We compute the policy gradient shown above4 in every training iteration—or gradient ascent step. This constitutes one epoch of the training process. Intuitively, this update rule works well because performing gradient ascent with the above estimate for the policy gradient increases the log probability of actions within a trajectory that achieves a large return. Notably, this simple formulation of the policy gradient is used by the REINFORCE algorithm [1], which is a well-known and widely-used baseline within RL literature.
An implementation. Now that we have a basic understanding of policy gradients, we can look at an example implementation. A great example of policy gradients is provided within OpenAI’s spinning up tutorial series for RL; see the link below. In this example, we can use one of several possible environments available within OpenAI’s gym package, the policy is implemented as a feed-forward neural network, and we can see a concrete example of a policy gradient being computed (in PyTorch) from a batch of experience data collected with our agent.
Variants of the Basic Policy Gradient
There are several variants of the policy gradient that can be derived. Each of these variants address issues associated with the simple policy gradient that we learned about in the previous section. We will now overview some of these variants to gain a better grasp of the different policy gradient algorithms that exist.
Reward-to-go trick. Our initial policy gradient expression (copied above) increases the probability of a given action based upon the total return of a trajectory, which is a sum of all (potentially discounted) rewards obtained along the entire trajectory. However, we might wonder: Why should we consider rewards that are obtained before this action is even taken? Shouldn’t we only encourage actions based on rewards obtained after they are taken? The short answer is yes—this simple change leads to a new variant of the policy gradient expression that is commonly referred to as the “reward-to-go” policy gradient5; see below.
We can derive the reward-to-go policy gradient using the expected grad-log-prob (EGLP) lemma. One of the main problems with our original expression for the policy gradient is that estimating this gradient accurately requires a large number of sample trajectories. Using the EGLP lemma, we can show that the reward-to-go policy gradient—despite not changing the expected value of the policy gradient—reduces the variance of our estimate and, therefore, reduces the total number of trajectories required to derive an accurate estimate of the policy gradient.
Adding a baseline. Going further with the EGLP lemma, we can use it to show that the modified expression above also maintains the desired expectation of the policy gradient, while (again) reducing the variance. Here, we add a baseline function to our expression that only depends on the current state. Interestingly, there are several useful functions that we can consider as a baseline. For example, we could use the on-policy value function, which characterizes the expected return for an agent starting in a given state and acting according to the current policy. In this case, the above expression would only positively reinforce trajectories that achieve an above average return (i.e., greater than the baseline).
Vanilla Policy Gradient
So far, we have seen three variants of the policy gradient; see above. The vanilla policy gradient has a similar structure to the formulations above, but it uses the advantage function as shown below. Again, this formulation of the policy gradient maintains the same expectation while reducing variance, meaning that we can accurately estimate the policy gradient with fewer sample trajectories.
Similarly to other policy gradient algorithms, we can estimate the above expression using a sample mean (i.e., by sampling several trajectories in practice and taking a discrete average of the quantities within the above expression) and optimize a policy with this estimate of the vanilla policy gradient via gradient ascent. Given that vanilla policy gradient is an on-policy algorithm, we do this by allowing the current policy to interact with the environment and collect a sufficient amount of data. Then, we i) collect these experiences into a mini-batch of data, ii) compute a sample estimate of the above policy gradient, and iii) update the parameters of our policy via gradient ascent. See below for pseudocode.
Estimating the advantage function. Although we have already discussed computing estimates of policy gradient via sampling, the expression for the vanilla policy gradient is a bit different from what we have seen so far due to its use of the advantage function. However, policy gradients are commonly formulated with the advantage function in RL, and various techniques have been proposed for deriving estimates of the advantage function. One of the most widely-used techniques is Generalized Advantage Estimation (GAE) [3]. The details of this technique are beyond the scope of this post, but the interested reader should see Section 3 of [3] for the derivation of this technique.
Connection to language models. Formulating the policy gradient with an advantage function is extremely common. In fact, RL algorithms that are commonly used for finetuning language models—such as trust region policy optimization (TRPO) [6] and proximal policy optimization (PPO) [7]—are also based upon a formulation of the policy gradient with an advantage function. Plus, both of these techniques use the GAE technique to estimate the advantage function as well! We will dive more into these more recent RL algorithms in future posts.
Takeaways
We should now have a basic grasp of policy gradients, how they are derived, and the common variants of policy gradients that are used by popular RL algorithms. Some high-level takeaways are summarized in the points below.
Policy optimization aims to learn a policy that maximizes the expected return over sampled trajectories. To learn this policy, we can use common gradient-based optimization algorithms, such as gradient ascent. However, doing this requires that we (approximately) compute the gradient of the expected return with respect to the current policy—the policy gradient; see above.
Basic policy gradient. The most simple formulation of the policy gradient is shown above. We can compute this expression in practice by taking a sample mean over trajectories that are gathered from the environment by acting according to our current policy. A simple policy gradient implementation will i) allow the current policy to interact and gather data from the environment, ii) use this data to estimate the policy gradient shown above, and iii) perform a gradient ascent update using this estimate.
Policy gradient variants. Unfortunately, the simplest variant of the policy gradient requires many trajectories to be sampled to generate an accurate estimate of the policy gradient. To mitigate this problem, several variants of the policy gradient can be derived, including the reward-to-go and baseline policy gradients. One especially notable formulation of the policy gradient, however, is the vanilla policy gradient (shown above). To estimate this quantity in practice, we can follow a similar approach as before. However, we need to adopt a specialized technique—such as GAE [4]—to estimate the advantage function.
New to the newsletter?
Hi! I’m Cameron R. Wolfe, deep learning Ph.D. and Director of AI at Rebuy. This is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews of relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on Medium, X, and LinkedIn!
Bibliography
[1] Simple statistical gradient-following algorithms for connectionist reinforcement learning, Williams, Machine learning 1992
[2] Sutton, Richard S., et al. "Policy gradient methods for reinforcement learning with function approximation." Advances in neural information processing systems 12 (1999).
[3] Schulman, John, et al. "High-dimensional continuous control using generalized advantage estimation." arXiv preprint arXiv:1506.02438 (2015).
[4] Schulman, John. Optimizing expectations: From deep reinforcement learning to stochastic computation graphs. Diss. UC Berkeley, 2016.
[5] Achiam, Josh. Spinning Up in Deep RL. OpenAI, 2018: https://spinningup.openai.com/en/latest/index.html
[6] Schulman, John, et al. "Trust region policy optimization." International conference on machine learning. PMLR, 2015.
[7] Schulman, John, et al. "Proximal policy optimization algorithms." arXiv preprint arXiv:1707.06347 (2017).
Remember, the environment specifies the transition function and reward in a model-free RL setup.
Gradient ascent uses addition, while gradient descent uses subtraction.
This is actually the area of research that I studied during my PhD! It is a really interesting field, as it lays the theoretical foundations for all of the practical algorithms that we use for training large neural networks today.
Here, the overline that we place over the gradient of the objective is used to indicate that we making an estimation. In other words, this is not an exact/analytical expression for the policy gradient.
For simplicity, we assume that the return is finite horizon, meaning that there are a total number of steps T in the trajectory, and that the return is undiscounted, meaning that there is no discount factor applied to the rewards when computing the return.