Decoder-Only Transformers: The Workhorse of Generative LLMs

Building the world's most influential neural network architecture from scratch...

Mar 04, 2024

The current pace of AI research is staggering. Keeping up with the most recent publications is a difficult feat, leaving even experts in the field feeling as if they are failing to grasp the finer details of this evolving frontier. In the domain of large language models (LLMs) especially, impactful research is being released constantly, including anything from new foundation models (e.g., Gemma [15] and OLMo [12]) to better alignment techniques (e.g., DPO [32] versus PPO [33] versus REINFORCE [34]) to exotic topics like model merging. Despite these rapid advancements, however, one component of LLMs has remained constant—the decoder-only transformer architecture. Shockingly, the architecture used by most modern LLMs is nearly identical to that of the original GPT model. We just make the model much larger, modify it slightly, and use a more extensive training (and alignment) process. For this reason, the decoder-only transformer architecture is one of the most fundamental and important ideas in AI research. Within this overview, we will comprehensively explain this architecture, implement all of its components from scratch, and explore how it has evolved in recent research.

The Self-Attention Operation

Given that the transformer architecture was proposed in a paper titled “Attention Is All You Need” [1], it probably comes as no surprise that self-attention is at the core of all modern language models. Put simply, self-attention transforms the representation of each token in a sequence based upon its relationship to other tokens in the sequence; see above. But, how exactly does this work? In this section, we will explain the concepts behind self-attention step-by-step, as well as build an implementation (in PyTorch) of the self-attention variant used by LLMs.

Understanding Scaled Dot Product Attention

“An attention function [maps] a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.” - from [1]

Projecting the input. The input to a self-attention layer is simply a batch of token sequences, where each token in the sequence is represented with a vector. Assuming we use a batch size B and each sequence is of length T, then our self-attention layer receives an tensor of shape [B, T, d] as input, where d is the dimensionality of the token vectors. For simplicity, we will first outline the self-attention operation using only one sequence of tokens as input; see below. However, the same concepts can be easily applied to a batch of sequences.

Sequence of token vectors in list and matrix form

The first step of self-attention is to perform three separate (linear) projections of the token vectors in our input sequence, forming key, query, and value vector sequences. To do this, we have three weight matrices—corresponding to the key, query, and value projections—that are used to project each of the input token vectors, forming new sequences of transformed token vectors. Because we do this three times, we end up with three separate sequences of token vectors; see below.

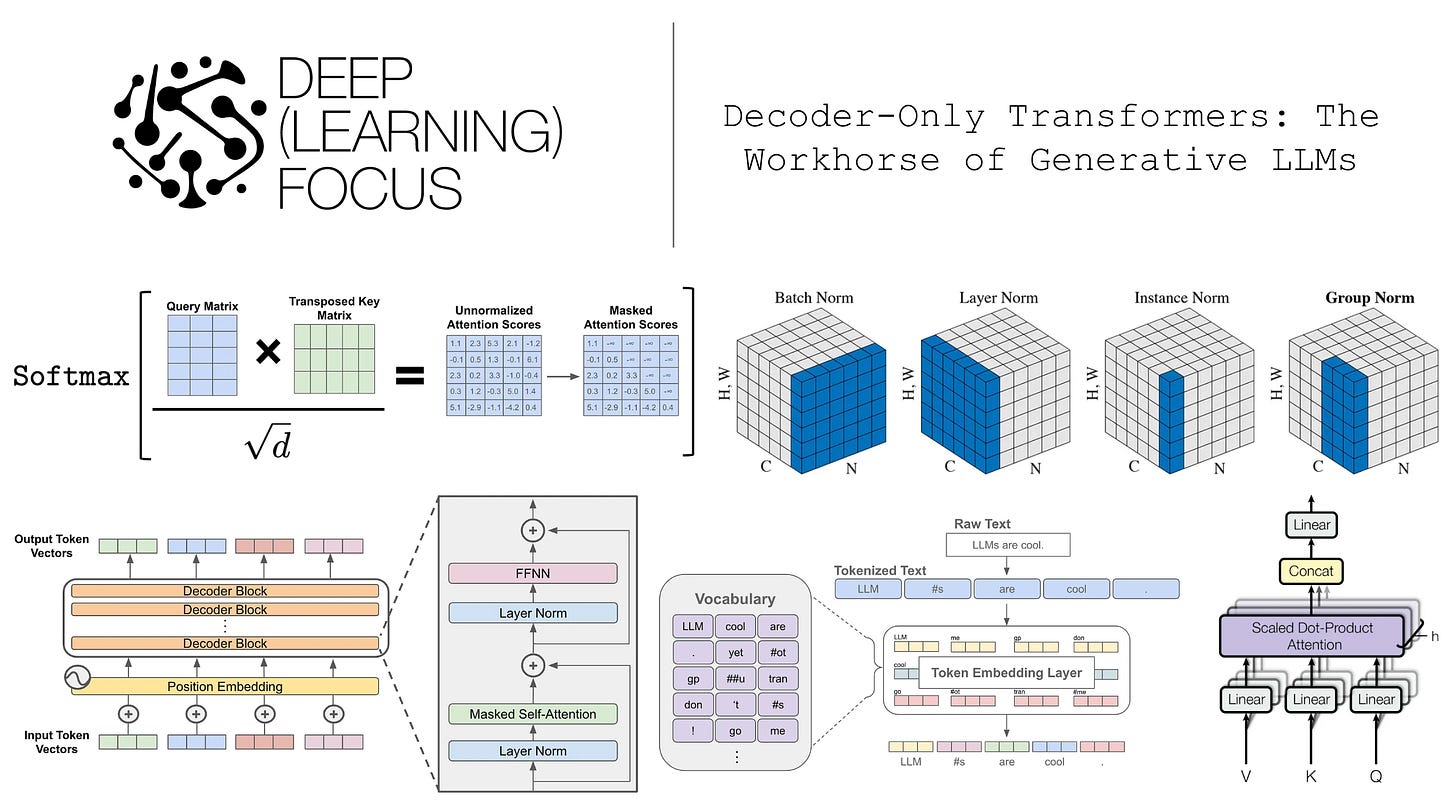
Creating the query, key, and token vectors

Computing attention scores. After projecting the input, attention scores are generated using the key and query vectors. We compute an attention score a[i, j] for every pair of tokens [i, j] within the sequence. Attention scores lie in the range [0, 1] and quantitatively characterize how much token j should be considered when computing the new representation for token i. Practically, we compute a[i, j] by taking the dot product of the query vector for token i with the key vector for token j; see below.

Computing attention scores from query and key vectors

We can efficiently compute all pairwise attention scores in a sequence by stacking the query and key vectors into two matrices and multiplying the query matrix with the transposed key matrix. The result of this operation is a matrix of size [T, T]—we will call this the attention matrix—that contains all pairwise attention scores in the sequence. From here, we divide each value in the attention matrix by the square root of d—an approach that has been found to improve training stability [1]—and apply a softmax operation to each row of the attention matrix; see below. After softmax has been applied, the attention scores for each token lie within the range [0, 1] and form a valid probability distribution.

Value vectors. Once we have the attention scores, deriving the output of self-attention is easy. The output for each token is simply a weighted combination of value vectors, where the weights are given by the attention scores. To compute this output in batch, we can simply stack all value vectors into a matrix and take the product of the attention matrix with the value matrix. Notably, self-attention preserves the size of its input—a transformed, d-dimensional output vector is produced for each token vector within the input. If we write out this matrix multiplication by hand, we will see that each token’s output representation is just a weighted average of value vectors with weights given by attention scores.

Causal Self-Attention for LLMs

The self-attention operation described above forms the basis of the transformer architecture. However, the transformer’s decoder uses a slightly more complex version of self-attention called masked, multi-headed self-attention. First, we will learn the differences between masked and bidirectional self-attention. Then, we will discuss how attention can be computed across multiple “heads” in parallel.

Masked self-attention. Decoder-only transformers use a variant of self-attention called masked (or causal) self-attention. While vanilla (or bidirectional) self-attention—as described in the previous section—allows all tokens within the sequence to be considered when computing attention scores, masked self-attention modifies the underlying attention pattern by “masking out” tokens that follow a given token within the sequence. For example, let’s consider our token sequence [“LLM”, “#s”, “are”, “cool”, “.”] and assume we are trying to compute attention scores for the token “are”. So far, we have learned that self-attention will compute an attention score between “are” and every other token within the sequence. With masked self-attention, however, we only compute attention scores for “LLM”, “#s”, and “are”. Masked self-attention prohibits us from looking forward in the sequence during self-attention.

Masking attention scores in causal self-attention

Masked self-attention is implemented similarly to bidirectional self-attention in practice. Once the query and key matrices have been multiplied, we have an attention matrix of size [T, T] with each token’s attention scores across the full sequence. Prior to performing the softmax operation across each row of this matrix, however, we can set all values above the diagonal of the attention matrix to negative infinity; see above. By doing this, we ensure that, for each token, all tokens that follow this token in the sequence are given an attention score of zero after the softmax operation has been applied. In other words, we mask each token’s attention scores to exclude any future tokens within the sequence.

Attention heads. The attention operation we have described so far uses softmax to normalize attention scores that are computed across the sequence. Although this approach forms a valid probability distribution, it also limits the ability of self-attention to focus on multiple positions within the sequence—the probability distribution can easily be dominated by one (or a few) words. To solve this issue, we typically compute attention across multiple “heads” in parallel; see below.

Within each head, the masked attention operation is identical. However, we i) use separate key, query, and value projections for each head and ii) reduce the dimension of the key, query, and value vectors to keep computational costs reasonable. Typically, we will change the dimensionality of these vectors from d to d // H1, where H is the number of attention heads. Using this approach, each attention head can learn a unique representational subspace and focus on different parts of the underlying sequence. Plus, we avoid added computational costs by reducing the dimension of vectors used by each attention head.

Finally, there’s one more detail that we have to consider with multi-headed self-attention: How do we combine the output of each head? Well, there are a variety of different options (e.g., concatenation, averaging, projecting, etc.). However, the vanilla implementation of multi-headed self-attention typically:

Concatenates the output of each head.
Linearly projects the concatenated output.

Because each attention head outputs token vectors of dimension d // H, the concatenated output of all attention heads has dimension d (i.e., same as the attention layer’s input dimension).

Implementing Causal Self-Attention in PyTorch

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

Show hidden characters

	"""
	Source: https://github.com/karpathy/nanoGPT/blob/master/model.py
	"""

	import math
	import torch
	from torch import nn
	import torch.nn.functional as F

	class CausalSelfAttention(nn.Module):

	def __init__(
	self,
	d,
	H,
	T,
	bias=False,
	dropout=0.2,
	):
	"""
	Arguments:
	d: size of embedding dimension
	H: number of attention heads
	T: maximum length of input sequences (in tokens)
	bias: whether or not to use bias in linear layers
	dropout: probability of dropout
	"""
	super().__init__()
	assert d % H == 0

	# key, query, value projections for all heads, but in a batch
	# output is 3X the dimension because it includes key, query and value
	self.c_attn = nn.Linear(d, 3*d, bias=bias)

	# projection of concatenated attention head outputs
	self.c_proj = nn.Linear(d, d, bias=bias)

	# dropout modules
	self.attn_dropout = nn.Dropout(dropout)
	self.resid_dropout = nn.Dropout(dropout)
	self.H = H
	self.d = d

	# causal mask to ensure that attention is only applied to
	# the left in the input sequence
	self.register_buffer("mask", torch.tril(torch.ones(T, T))
	.view(1, 1, T, T))

	def forward(self, x):
	B, T, _ = x.size() # batch size, sequence length, embedding dimensionality

	# compute query, key, and value vectors for all heads in batch
	# split the output into separate query, key, and value tensors
	q, k, v = self.c_attn(x).split(self.d, dim=2) # [B, T, d]

	# reshape tensor into sequences of smaller token vectors for each head
	k = k.view(B, T, self.H, self.d // self.H).transpose(1, 2) # [B, H, T, d // H]
	q = q.view(B, T, self.H, self.d // self.H).transpose(1, 2)
	v = v.view(B, T, self.H, self.d // self.H).transpose(1, 2)

	# compute the attention matrix, perform masking, and apply dropout
	att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1))) # [B, H, T, T]
	att = att.masked_fill(self.mask[:,:,:T,:T] == 0, float('-inf'))
	att = F.softmax(att, dim=-1)
	att = self.attn_dropout(att)

	# compute output vectors for each token
	y = att @ v # [B, H, T, d // H]

	# concatenate outputs from each attention head and linearly project
	y = y.transpose(1, 2).contiguous().view(B, T, self.d)
	y = self.resid_dropout(self.c_proj(y))
	return y

view raw causal_self_attention.py hosted with ❤ by GitHub

The implementation of masked, multi-headed self-attention (full code is shown above) should be pretty easy to follow if we have understood the discussion up to this point! First, we perform the key, query, and value projections using a simple linear layer in PyTorch. We can perform the key, query, and value projections for all self-attention heads using a single linear layer! This layer takes a sequence of token embeddings of dimension d as input and produces token embeddings of size 3 * d as output. From here, we can split the output into sequences of d-dimensional key, query, and value vectors. Then, each d-dimensional vector can be reshaped into H smaller vectors—one for each attention head—and we can transpose the tensor to yield an output of shape [B, H, T, d // H], where B is the number of sequences in the batch being processed; see below.

q, k, v  = self.c_attn(x).split(self.d, dim=2)
k = k.view(B, T, self.H, self.d // self.H).transpose(1, 2)
q = q.view(B, T, self.H, self.d // self.H).transpose(1, 2)
v = v.view(B, T, self.H, self.d // self.H).transpose(1, 2)

From here, we can compute attention scores across all tokens within each head and across the entire batch using basic matrix/tensor multiplication. First, we multiply the query tensor by the transpose of the key matrix, thus computing the unnormalized attention matrix of size [B, H, T, T]. We then divide this result by sqrt(d) and apply softmax over the last dimension, thus transforming each token’s attention scores across the sequence into a probability distribution. Prior to the softmax, however, we fill all entries of the attention matrix above the diagonal with a value of negative infinity; see below.

att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
att = att.masked_fill(self.mask[:,:,:T,:T] == 0, float('-inf'))
att = F.softmax(att, dim=-1)
att = self.attn_dropout(att)

Optionally, we can also perform dropout on attention scores [2]2, which has been shown to regularize the training process and improve generalization. Once the attention matrix has been computed, we can derive the final output of self-attention by multiplying the attention matrix with the value matrix, which takes a weighted average of value vectors for each token based on attention scores. The result of this computation is a tensor of size [B, H, T, d // H], but we can concatenate the output of each attention head by simply transposing and reshaping the tensor to be of size[B, T, d]; see below.

y = att @ v
y = y.transpose(1, 2).contiguous().view(B, T, self.d)
y = self.resid_dropout(self.c_proj(y))

Finally, we perform one last linear projection of this concatenated output (optionally with dropout) to get our final result, as shown in the code above.

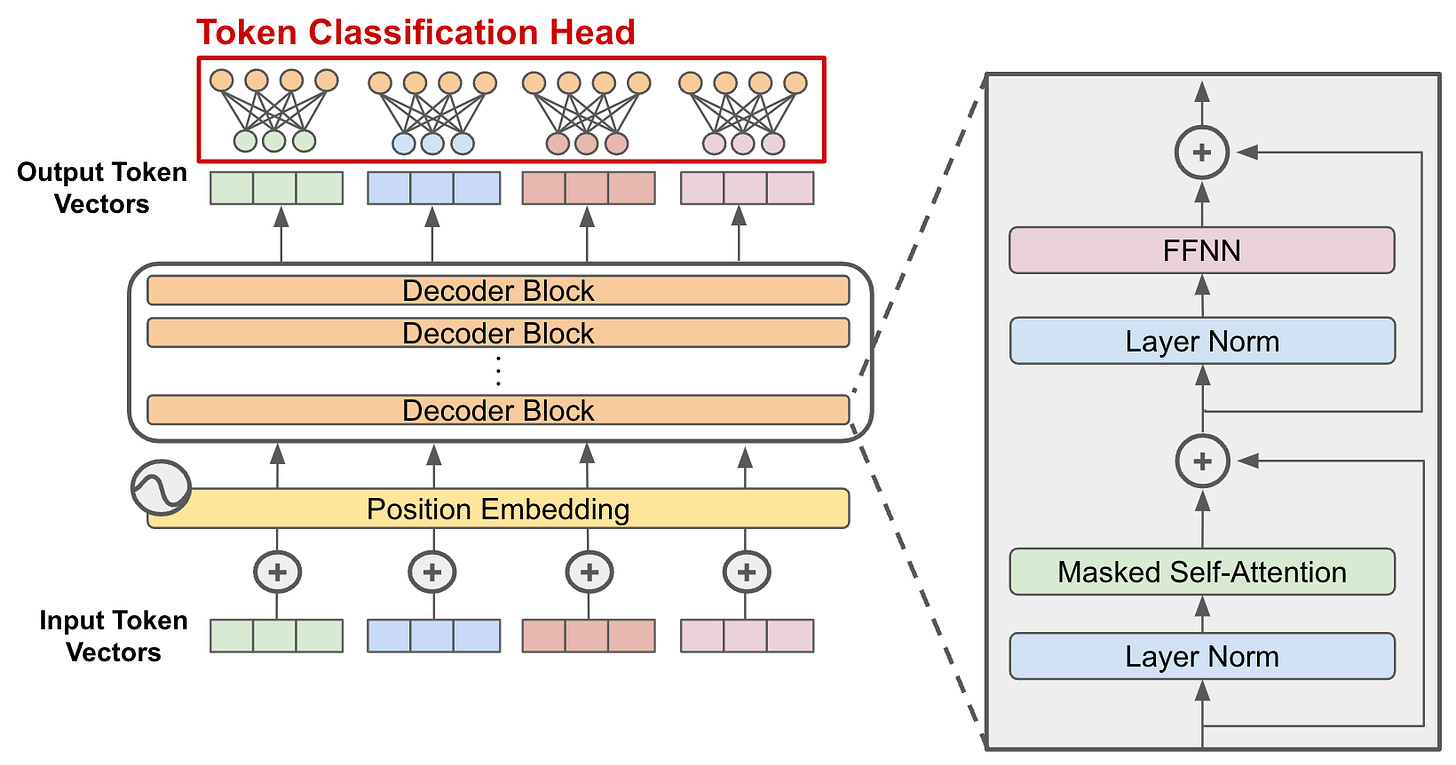
The Decoder-Only Transformer Block

The decoder-only transformer architecture is comprised of several “blocks” with identical structure that are stacked in sequence. Within each of these blocks, there are two primary components:

Masked, multi-headed self-attention.
A feed-forward transformation.

Additionally, we usually surround these components with a residual connection and a normalization layer. Within this section, we will discuss this block structure in more detail and provide a concrete implementation in PyTorch.

Layer Normalization

Although high-performance GPUs and advancements in model architectures may make us think otherwise, training large, deep neural networks has not always been a breeze! Early attempts at training neural networks with many layers were largely unsuccessful due to issues with vanishing, exploding, and unstable gradients. Several advancements have been proposed to address these issues:

Better methods of initializing weights (e.g., Xavier or He initialization).
Replacing sigmoid activation functions with ReLU [5] (i.e., this keeps gradients in the activation function from becoming very small).
Normalizing intermediate neural network activations [6].

Within this section, we will focus on the final advancement mentioned above—normalization. The motivation behind normalization is quite simple. The intermediate activation values of a deep neural network can become unstable (i.e., very large or very small) because we repeatedly multiply them by a matrix of model parameters. For example, if we run the PyTorch code snippet below, we will see that repeating the same (random) matrix multiplication many times in a row causes the values of our output to become incredibly large!

Show hidden characters

	import torch

	# experiment settings
	d = 5
	nlayers = 100
	normalize = False # set True to use normalization

	# create vector with random entries between [-1, 1]
	input_vector = (torch.rand(d) - 0.5) * 2.0

	# create matrix with random entries between [-1, 1]
	# by which we can repeatedly multiply the input vector
	weight_matrix = (torch.rand(d, d) - 0.5) * 2.0

	output = input_vector
	for i in range(nlayers):
	# optionally perform normalization
	if normalize:
	output = (output - torch.mean(output)) / torch.std(output)

	# repeatedly multiply the vector by the matrix
	output = weight_matrix @ output

	# observe output values
	print(output)

view raw exploding_activations.py hosted with ❤ by GitHub

To solve this, we can normalize3 the activation values between each matrix multiplication, allowing activation values to remain stable over time. This is exactly the idea that is used by normalization layers within a neural network. Let’s take a look at a few popular variants of normalization that exist.

Normalization variants. Depending up the domain and architecture being used, there are several normalization techniques that we can adopt. The two most common forms of normalization are4:

Batch Normalization [6]
Layer Normalization [7]

These techniques are quite similar. For both of them, we just transform activation values using the equation shown below. The difference between them lies in how we choose to compute the mean and standard deviation.

Batch normalization—as the name indicates—computes a per-dimension mean and standard deviation over the entire mini-batch; see below. Although this approach works well, it is limited by the fact that we must process a sufficiently large mini-batch of inputs to get a reliable estimate of the mean and variance. This becomes an issue during inference, where processing only a small number of input examples at once is common. For this reason, we must compute a running estimate5 of the mean and standard deviation during training that can be used for inference. Nonetheless, batch normalization is widely used and is the standard choice of normalization technique within computer vision applications.

Layer normalization eliminates batch normalization’s dependence upon the batch dimension by computing the mean and standard deviation over the final dimension of the input. In the case of decoder-only transformers, this means that we compute normalization statistics over the embedding dimension; see above.

Currently, batch normalization is commonly used for computer vision tasks, while layer normalization is standard for natural language processing tasks. The original transformer architecture adopted layer normalization within its implementation [10], and this choice has been a standard for the transformer ever since. However, layer normalization was also used by earlier language models—those based on recurrent neural networks6—prior to the proposal of the transformer.

Affine transformation. Normalization layers in deep networks are also typically combined with an affine transformation. This might sound complicated, but it just means that we modify layer normalization as shown in the equation below. After normalizing the activation value, we multiply it by a constant γ, as well as add a constant β. Both of these constants are learnable and treated the same as a normal model parameter. Additionally, we see below that layer normalization uses a slightly modified form of standard deviation in the denominator that incorporates a small, fixed constant ε to avoid issues with dividing by zero.

Layer normalization with an affine transformation

Layer normalization is implemented in PyTorch and can be easily accessed either via the associated module or its functional form.

Feed-Forward Transformation

Each decoder-only transformer block contains a pointwise7 feed-forward transformation; see above. This transformation passes every token vector within its input through a small, feed-forward neural network. This neural network consists of two linear layers—with optional bias8—that are separated by a non-linear activation function. The neural network’s hidden dimension is usually larger—4X larger in the case of GPT [3], GPT-2 [4], and many other LLMs—than the dimension of the token vector it takes as input.

Activation function. Which activation function should we use in an LLM’s feed-forward layers? In [13], authors compare the performance of numerous activation functions, finding that the SwiGLU activation (shown above) yields the best performance given a fixed amount of compute. For this reason, SwiGLU is commonly used by popular LLMs like LLaMA-2 [11] and OLMo [12]. However, not all LLMs use SwiGLU; e.g., both Falcon [14] and Gemma [15] use GeLU.

Show hidden characters

	"""
	Source: https://github.com/karpathy/nanoGPT/blob/master/model.py
	"""

	from torch import nn

	class FFNN(nn.Module):

	def __init__(
	self,
	d,
	bias=False,
	dropout=0.2,
	):
	"""
	Arguments:
	d: size of embedding dimension
	bias: whether or not to use bias in linear layers
	dropout: probability of dropout
	"""
	super().__init__()
	self.c_fc = nn.Linear(d, 4 * d, bias=bias)
	self.gelu = nn.GELU()
	self.c_proj = nn.Linear(4 * d, d, bias=bias)
	self.dropout = nn.Dropout(dropout)

	def forward(self, x):
	x = self.c_fc(x) # [B, T, 4*d]
	x = self.gelu(x)
	x = self.c_proj(x) # [B, T, d]
	x = self.dropout(x)
	return x

view raw transformer_ffnn.py hosted with ❤ by GitHub

Implementation in PyTorch. Implementing the feed-forward component of a transformer block is simple; see above. We just need a few linear layers with an activation function in between. In the above implementation, an input of size [B, T, d] is provided to the first linear layer, which has an input dimension of d and an output dimension of h = 4 * d. The first linear layer performs a batched matrix multiplication of all d-dimensional vectors in this input by a matrix of size d x h, forming an output of size [B, T, h]. From here, we apply the non-linear activation function to this output and pass it through the next linear layer, which has an input dimension of h and an output dimension of d. Finally, we can (optionally) apply dropout to the output of the second linear layer, which has size [B, T, d], to regularize the model during training.

Residual Connections

We typically add residual connections between each of the self-attention and feed-forward sub-layers of the transformer block. The concept of a residual connection was originally proposed by the ResNet architecture [16], which is a widely used (and famous) convolutional neural network architecture for computer vision tasks like image classification and object detection. Residual connections are simple to understand conceptually. Instead of just passing neural network activations through a layer in the network, we i) store the input to the layer, ii) compute the layer’s output, and iii) add the layer’s input to the layer’s output; see below.

A generic neural network layer with a residual connection

Residual connections are a generic idea that can be applied to any neural network layer that does not change the dimension of the input9. By adding residual connections, we can mitigate problems with vanishing and exploding gradients, as well as improve the overall ease and stability of the training process. Residual connections provide a “shortcut” that allows gradients to flow freely through the network during backpropagation10. The benefits of residual connections have been extensively explored and analyzed within deep learning literature, leading to a variety of interesting intuitions regarding their utility [17, 18, 19].

Putting It All Together!

To construct a full decoder-only transformer block, we have to use all of the components that we have talked about so far:

Masked, multi-headed self-attention
Layer normalization
Pointwise feed-forward transformation
Residual Connections

The layout of a decoder-only transformer block is shown in the figure above. As we will soon learn, the exact layout of the block may change depending upon the implementation. However, the schematic above matches the vanilla structure of decoder-only transformer blocks used by most GPT-style LLMs. This same structure of decoder-only transformer block is implemented in PyTorch below.

Show hidden characters

	"""
	Source: https://github.com/karpathy/nanoGPT/blob/master/model.py
	"""

	from torch import nn

	class Block(nn.Module):
	def __init__(
	self,
	d,
	H,
	T,
	bias=False,
	dropout=0.2,
	):
	"""
	Arguments:
	d: size of embedding dimension
	H: number of attention heads
	T: maximum length of input sequences (in tokens)
	bias: whether or not to use bias in linear layers
	dropout: probability of dropout
	"""
	super().__init__()
	self.ln_1 = nn.LayerNorm(d)
	self.attn = CausalSelfAttention(d, H, T, bias, dropout)
	self.ln_2 = nn.LayerNorm(d)
	self.ffnn = FFNN(d, bias, dropout)

	def forward(self, x):
	x = x + self.attn(self.ln_1(x))
	x = x + self.ffnn(self.ln_2(x))
	return x

view raw decoder_only_block.py hosted with ❤ by GitHub

The Decoder-Only Transformer

We will now take a look at the full decoder-only transformer architecture, which is primarily composed the building blocks we have seen so far. However, there are a few extra details that we have to cover, such as constructing the model’s input and using the model’s output to predict/generate text. Compared to self-attention, these details are relatively simple to understand, but covering them is necessary to get the full picture of how a decoder-only transformer architecture operates.

Constructing the Model’s Input

As outlined previously, the input to a transformer block is expected to be a (batched) sequence of token vectors, usually in the form of a tensor with shape [B, T, d]. However, the LLM usually receives input in the form of a textual prompt. How do we convert this textual prompt into a sequence of token vectors?

Tokenization. The transformer receives raw text as input. The first step in processing this text is to tokenize it, or convert it into a series of discrete words or sub-words. These words and sub-words are commonly called tokens; see below.

Converting raw text into a sequence of tokens

The tokenization process is handled by the model’s tokenizer, which uses an algorithm like Byte-Pair Encoding (BPE) [20], SentencePiece [21], or WordPiece [22] to break text into sequences of tokens; see here for more details. The tokenizer has a fixed-size vocabulary—usually containing around 50K to 300K unique tokens—that defines the set of known tokens that can be formed from a raw sequence of text. The tokenizer has its own training pipeline that derives its underlying vocabulary and typically implements two major functions:

Encode: convert a string into a sequence of tokens
Decode: convert a sequence of tokens into a string

Tokenization is an oftentimes overlooked aspect of LLM training and usage. However, failing to investigate and understand the tokenization process for an LLM is a huge mistake! Tokenization is the first step in creating the model’s input and, therefore, has a massive impact on the downstream model’s performance. Issues with an LLM can often be traced back to nuanced bugs in the tokenization process that are difficult to detect11. As such, I would highly encourage the interested reader to dive deeper into the tokenization process. For an in-depth and practical overview of BPE tokenizers—the most commonly-used tokenizers for LLMs—check out the recently published video below from Andrej Karpathy.

Building GPT's Tokenizer

Token embeddings. Once we have tokenized our text and formed a sequence of tokens, we must convert each of these tokens into a corresponding embedding vector. To do this, we create an embedding layer, which is a part of the decoder-only transformer model. This embedding layer is just a matrix with d columns and V rows, where V is the size of the tokenizer’s vocabulary. Each token within the vocabulary is associated with an integer index that corresponds to a row in this embedding matrix. We can convert tokens into a d-dimensional embedding by simply looking up the token’s entry in this embedding layer; see below.

Looking up token embeddings in an embedding layer

This embedding layer is trained during the LLM’s training process similarly to any other model parameters! Token embeddings are not fixed, but rather learned from data.

Position embeddings. Now, we have converted our raw text into a sequence of token vectors. If we do this for an entire batch of textual sequences, we will have the input of size [B, T, d] expected by our transformer blocks. However, there is one final step that we need to perform—positional embedding.

“Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence.” - from [1]

In studying the self-attention mechanism, we might notice that the position of each token in the sequence is not considered when computing the output12! However, the order of words within a sequence of text is obviously important (e.g., “I have to read this book.” vs. “I have this book to read.”). Therefore, we need some way of injecting positional information into the self-attention process. In [1], this was done by adding positional embeddings of dimension d to each token within the model’s input. Because each position within the sequence has a unique position embedding, the position of each token can be distinguished.

Similarly to token embeddings, we can store position embeddings in an embedding layer and learn them from data during the LLM’s training process—this approach is simple to implement. Alternatively, we can generate fixed token embeddings via some rule or equation. In [1], positional embeddings are generated using sine and cosine functions, as shown within the figure below.

Generating positional embeddings with sine and cosine functions (from [1])

These approaches are referred to as “absolute” positional embedding strategies, as the embedding being used is determined by the token’s absolute position in the sequence. As we will see later in this post, absolute positional embedding strategies fail to generalize to sequences that are longer than those seen during training, which has led to the proposal of more generalizable strategies.

The Full Decoder-Only Transformer Model

Structure of a decoder-only transformer model

Once we have constructed the model’s input, we simply pass this input through a sequence of decoder-only transformer blocks; see above. The total number of transformer blocks depends on the size of the model; e.g., OLMo-7B [12] has 32 layers and OLMo-65B has 80 layers; see below. Transformer blocks preserve the size of their input, so the output of the model’s body—including all transformer blocks—is a sequence of token vectors that is the same size as the input.

Increasing the number of transformer blocks/layers within the underlying LLM is one of the primary ways of increasing the size of the model. Alternatively, we can increase the value of d (i.e., the dimension of token embeddings), which increases the size of weight matrices for all attention and feed-forward layers in the model. As shown above, we typically scale up the size of a decoder-only transformer by simultaneously increasing both i) the number of layers and ii) the hidden dimension. Oftentimes, we also increase the number of heads within each attention layer, but this does not impact the number of parameters in the model if we assume that each attention head has a dimension of d // H.

Classification head. Finally, there is one final detail of the decoder-only transformer architecture that we have to consider. Once we have passed our input sequence through the model’s body, we receive as output a same-size sequence of token vectors. To generate text or perform next token prediction (see here for more details on this process), we convert each token vector into a probability distribution over potential next tokens. To do this, we can add one extra linear layer with input dimension d and output dimension V (i.e., size of the vocabulary), which serves as a classification head, to the end of the model; see below.

Adding a classification head to the decoder-only transformer

Using this linear layer, we can convert each token vector in our output into a probability distribution over the token vocabulary. From the probability distribution over tokens, we can perform:

Next token prediction: the LLM pretraining objective that trains the model to predict the next token for every token within the input sequence using a cross entropy loss function.
Inference: autoregressively sample the best next token13 to generate based upon the token distribution generated by the model.

Show hidden characters

	"""
	Source: https://github.com/karpathy/nanoGPT/blob/master/model.py
	"""

	import torch
	from torch import nn
	import torch.nn.functional as F

	class GPT(nn.Module):

	def __init__(self,
	d,
	H,
	T,
	V,
	layers,
	bias=False,
	dropout=0.2,
	):
	"""
	Arguments:
	d: size of embedding dimension
	H: number of attention heads
	T: maximum length of input sequences (in tokens)
	V: size of the token vocabulary
	layers: number of decoder-only blocks
	bias: whether or not to use bias in linear layers
	dropout: probability of dropout
	"""
	super().__init__()
	self.transformer = nn.ModuleDict(dict(
	wte=nn.Embedding(V, d), # token embeddings
	wpe=nn.Embedding(T, d), # position embeddings
	drop=nn.Dropout(dropout),
	blocks=nn.ModuleList([Block(d, H, T, bias, dropout) for _ in range(layers)]),
	ln_f=nn.LayerNorm(d),
	head=nn.Linear(d, V, bias=bias),
	))

	def forward(self, idx, targets=None):
	# idx is a [B, T] matrix of token indices
	# targets is a [B, T] matrix of target (next) token indices
	device = idx.device
	_, T = idx.size() # [B, T]
	pos = torch.arange(0, T, dtype=torch.long, device=device)

	# generate token and position embeddings
	tok_emb = self.transformer.wte(idx) # [B, T, d]
	pos_emb = self.transformer.wpe(pos) # [T, d]
	x = self.transformer.drop(tok_emb + pos_emb)

	# pass through all decoder-only blocks
	for block in self.transformer.blocks:
	x = block(x)
	x = self.transformer.ln_f(x) # final layer norm

	if targets is not None:
	# compute the loss if we are given targets
	logits = self.transformer.head(x)
	loss = F.cross_entropy(
	logits.view(-1, logits.size(-1)),
	targets.view(-1),
	ignore_index=-1,
	)
	else:
	# only look at last token if performing inference
	logits = self.transformer.head(x[:, [-1], :])
	loss = None

	return logits, loss

view raw gpt.py hosted with ❤ by GitHub

Full architecture (in PyTorch). The full implementation of the decoder-only transformer architecture is depicted above. Given that we have already discussed each component of this architecture, the code above should be relatively straightforward. The only modifications that are made are:

Applying dropout to token and position embeddings prior to passing them as input to the first decoder-only transformer block.
The addition of a final layer normalization module that normalizes the output of the decoder-only transformer blocks prior to the classification head.

Once we have passed our input through all decoder-only transformer blocks, we can either pass all output token embeddings through the linear classification layer, allowing us to apply a next token prediction loss across the entire sequence (i.e., done during pretraining). Or, we can only pass the final output token embedding through the linear classification layer, which allows us to sample the next token to include in the model’s generated output (i.e., done during inference).

Modern Variants of the Architecture

Now that we understand the decoder-only transformer architecture, we can look at some of the variants of this architecture being used by modern LLMs. In most cases, the core details of the decoder-only transformer are maintained. However, the recent spike of interest in generative LLMs has produced a variety of useful modification to the decoder-only transformer that improve performance, boost speed (both during training and inference), make the training process more stable, allow the model to handle longer input sequences, and much more.

Transformer Block Layouts

The layout of the decoder-only transformer block that we have seen so far is the standard transformer block configuration. However, the order of normalization operations within this block may change depending upon the implementation. For example, we can see in the figure above that layer normalization operations are depicted as coming after the attention and feed-forward layers in the original transformer architecture [1]. Additionally, some architectures perform normalization at both locations; e.g., Gemma [15] normalizes both the input and the output of each transformer sub-layer, as explained below.

“We normalize both input and output of each transformer sub-layer, a deviation from the standard practice of solely normalizing one or the other.” - from [15]

Parallel blocks. Alternative block structures have been explored within the literature as well. For example, Falcon [14] and PaLM [24] use a parallel transformer block structure that passes input through the attention and feed-forward layers in parallel instead of in sequence; see below. Such an approach lessens the communication costs of distributed training14 and is found by both models to yield no noticeable degradation in performance.

Normalization Strategies

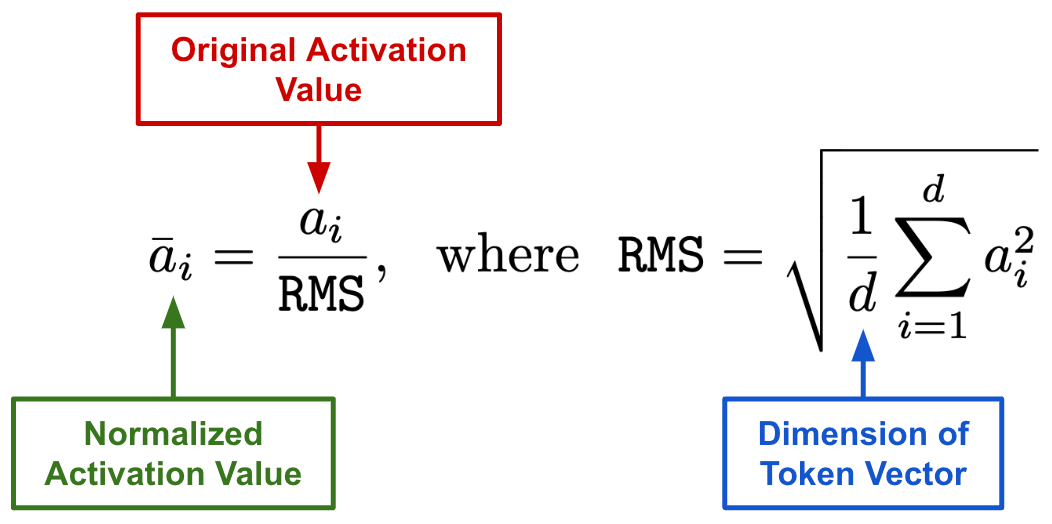
In addition to changing the exact location of normalization layers within the transformer block, the normalization strategy used varies between different models. While most models use layer normalization, Root Mean Square Layer Normalization [29] (RMSNorm for short!) is also popular. RMSNorm, which is formulated as shown above, is just a simplified version of layer normalization that has been shown to improve training stability and generalization. Plus, RMSNorm is 10-50% more efficient than layer normalization despite performing similarly, which has led models like LLaMA [30] and LLaMA-2 [11] to adopt this approach.

Better layer normalization. Going further, certain LLMs have adopted modified forms of layer normalization. For example, MPT [26] models use low precision layer normalization to improve hardware utilization during training, though this approach may cause loss spikes to arise in rare cases. Similarly, many LLMs (e.g., OLMo [12], LLaMA-2 [11], and PaLM [24]) exclude the bias terms within layer normalization; see below. In fact, many of these models also exclude bias from all layers of the transformer altogether! Excluding bias terms within the transformer maintains or improves the LLM’s performance and yields a (modest) speedup.

Efficient (Masked) Self-Attention

Although self-attention is the foundation of the transformer architecture, this operation is somewhat inefficient—it is an O(N^2) operation! For this reason, a plethora of efficient attention variants have been proposed; Reformer, SMYRF, and Performer to name a few. Many of these techniques theoretically reduce the complexity of self-attention to O(N), but they fail to achieve measurable speedups in practice. To solve this issue, FlashAttention [25] reformulates the self-attention operation in an efficient and IO-aware manner; see below.

The inner workings of FlashAttention are mostly hardware-related; see here for more details. However, the result is a drop-in replacement for the self-attention operation that has a variety of awesome benefits:

Speeds up BERT-large training time by 15%.
Improves training speed by 3X for GPT-2.
Enables longer context lengths for LLMs (due to better memory efficiency).

After the PyTorch 2.0 release, scaled dot product attention—this is the variant of self-attention we learned about in this post—can be replaced with FlashAttention to improve efficiency15! For this reason, many recent LLMs (e.g., Falcon [14] and MPT [26]) use FlashAttention. Plus, there is still active research being published in this area, which has resulted in some interesting developments:

FlashAttention-2: modifies FlashAttention to yield further gains in efficiency.
FlashDecoding: an extension of FlashAttention that focuses upon improving inference efficiency in addition to training efficiency.
Multi-query attention shares key and value projections between attention heads (from [1])

Multi and Grouped Query Attention. Beyond FlashAttention, several recent LLMs (e.g., Gemini [27], Falcon [14], and PaLM [24]) use multi-query attention, an efficient self-attention implementation that shares key and value projections between all attention heads in a layer; see above. Instead of performing a separate projection for each head, all heads share the same projection matrix for keys and the same projection matrix for values. This change does not make training any faster, but it significantly improves the inference speed of the resulting LLM.

Unfortunately, multi-query attention can cause slight deteriorations in performance, which led some LLMS (e.g., LLaMA-2) to search for alternatives. Instead of sharing all key and value projections across attention heads, grouped-query attention (GQA) [28] divides the H total self-attention heads into groups and shares key/value projections within the same group; see above. Such an approach is an interpolation between vanilla multi-headed self-attention and multi-query attention, which uses a shared key and value projection across all H heads. Interestingly, GQA maintains the performance of vanilla multi-headed causal self-attention and achieves comparable efficiency compared to multi-query attention.

Better Positional Embeddings

“We find that transformer language models (LMs) that use sinusoidal position embeddings have very weak extrapolation abilities.” - from [31]

The position embedding technique we have learned about so far uses additive positional embeddings determined by the absolute position of each token in a sequence. Although this approach is simple, it limits the model’s ability to generalize to sequences longer than those seen during training. As a result, we must pretrain the LLM over longer sequences (i.e., this can be quite expensive) if we need to accept longer inputs at inference time. For this reason, a variety of alternative position encoding schemes were proposed, including relative position embeddings that only consider the distance between tokens rather than their absolute position. Here, we will study two of the most commonly used strategies for injecting position information into an LLM—RoPE [23] and ALiBi [31].

Rotary Positional Embeddings (RoPE) [23] are a hybrid of absolute and relative positional embeddings that incorporate position into self-attention by:

Encoding absolute position with a rotation matrix.
Adding relative position information directly into the self-attention operation.

Notably, RoPE injects position information at every layer of the transformer, rather than just the model’s input sequence. Such an approach is found to yield a balance between absolute and relative position information, provides flexibility to expand to longer sequence lengths, and has decaying inter-token dependency as relative distances increase (i.e., tokens that are far apart pay less attention to each other). RoPE has gained in popularity recently, leading in its use in popular LLMs like PaLM16 [24], Falcon [14], OLMo [12], LLaMA/LLaMA-2 [11, 30], and more!

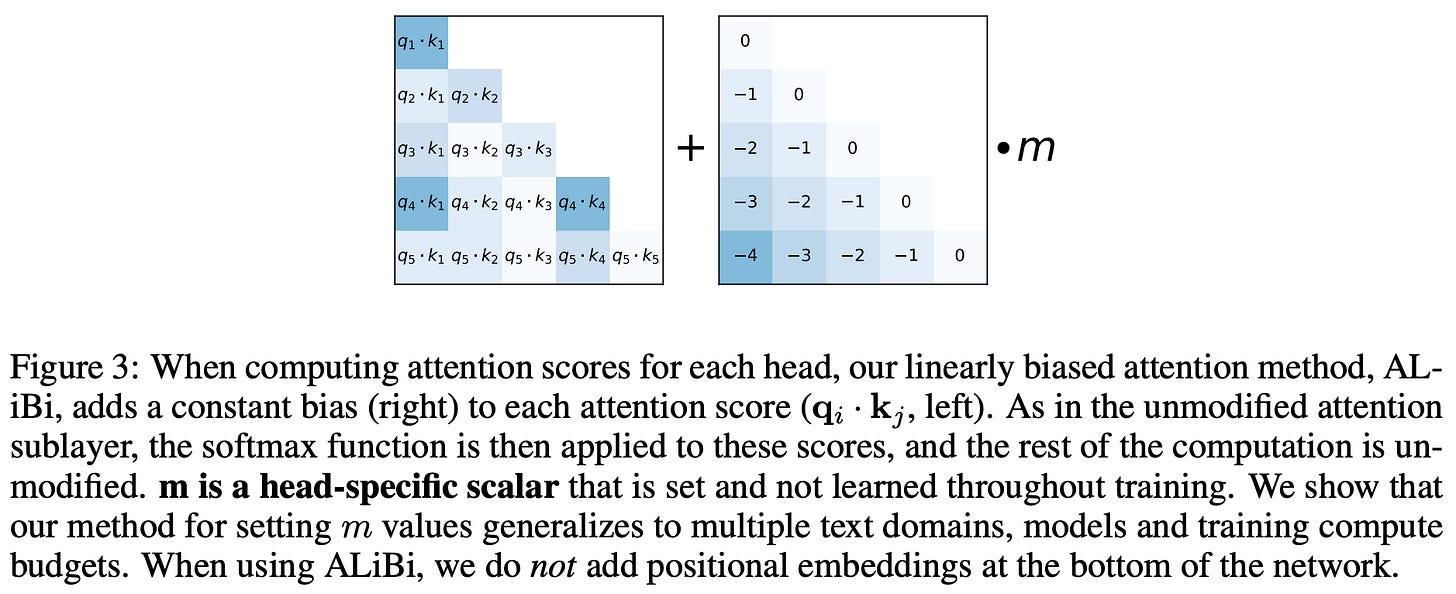
Attention with Linear Biases [31] is a follow-up technique that was proposed to improve the extrapolation abilities of position embedding strategies. Instead of using position embeddings, ALiBi incorporates position information directly into self-attention at each layer of the transformer by adding a static, non-learned bias to the attention matrix; see above. We compute the attention matrix normally (i.e., as a product of the query and key matrices) but add a constant bias to the values of the attention matrix that penalizes scores between more distant queries and keys. We can implement this approach very easily by adding these extra biases to the attention mask that is used for computing causal self-attention.

Despite its simplicity, this approach outperforms both vanilla position embedding techniques and RoPE in terms of extrapolating to sequences longer than those seen in training; see above. Plus, compute and memory costs are not increased significantly. ALiBi was adopted by the MPT models [26], which were finetuned to support input lengths up to (and exceeding) 65K tokens!

Takeaways

Despite the staggering pace of innovation, decoder-only transformers remain the cornerstone of research on generative LLMs. In fact, model architectures used by most modern LLMs, though much larger and modified in nuanced ways, largely match the architecture of the original GPT model [3]. As such, building a working understanding of the decoder-only transformer architecture is an absolute necessity for anyone interested in better understanding the inner workings of a language model. From the information in this overview, we can decompose our understanding of decoder-only transformer models into the following core ideas.

Constructing the input. Decoder-only transformers receive a textual prompt as input. First, we use a tokenizer—based upon an algorithm like Byte-Pair Encoding—to break this text into discrete tokens. Then, we map each of these tokens to a corresponding token vector stored within an embedding layer. This process forms a sequence of token vectors that are passed to the model as input. Optionally, we can augment these token vectors with additive positional embeddings.

Causal self-attention is the core of the decoder-only transformer and allows the model to learn from relationships between tokens in the input. The vanilla self-attention operation transforms each token’s representation by taking a weighted combination of other token representations, where weights are given by pairwise attention (or importance) scores between tokens. Causal self-attention follows a similar strategy but only computes attention scores for preceding tokens in the sequence. Attention is performed in parallel across several heads, each of which can focus upon different parts of the input sequence.

Feed-forward transformations are performed within each block of the decoder-only transformer, allowing us to individually transform each token’s representation. This feed-forward component is a small neural network that is applied in a pointwise manner to each token vector. Given a token vector as input, we pass this vector through a linear projection that increases its size by ~4X, apply a non-linear activation function (e.g., SwiGLU or GeLU), then perform another linear projection that restores the original size of the token vector.

Transformer blocks are stacked in sequence to form the body of the decoder-only transformer architecture. The exact layout of the decoder-only transformer block may change depending upon the implementation, but two primary sub-layers are always present:

Causal self-attention
Feed-forward transformation

Additionally, these sub-layers are surrounded by a layer normalization module—either before or after the sub-layer (or both!)—and a residual connection.

Classification head. The decoder-only transformer has one final classification head that takes token vectors from the transformer’s final output layer as input and outputs a vector with the same size as the vocabulary of the model’s tokenizer. This vector can be used to either train the LLM via next token prediction or generate text at inference time via sampling strategies like nucleus sampling and beam search.

New to the newsletter?

Hi! I’m Cameron R. Wolfe, and this is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews of relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on Medium, X, and LinkedIn!

Bibliography

[1] Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).

[2] Zehui, Lin, et al. "Dropattention: A regularization method for fully-connected self-attention networks." arXiv preprint arXiv:1907.11065 (2019).

[3] Radford, Alec, et al. "Improving language understanding by generative pre-training." (2018).

[4] Radford, Alec, et al. "Language Models are Unsupervised Multitask Learners."

[5] Glorot, Xavier, and Yoshua Bengio. "Understanding the difficulty of training deep feedforward neural networks." Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR Workshop and Conference Proceedings, 2010.

[6] Ioffe, Sergey, and Christian Szegedy. "Batch normalization: Accelerating deep network training by reducing internal covariate shift." International conference on machine learning. pmlr, 2015.

[7] Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E. Hinton. "Layer normalization." arXiv preprint arXiv:1607.06450 (2016).

[8] Wu, Yuxin, and Kaiming He. "Group normalization." Proceedings of the European conference on computer vision (ECCV). 2018.

[9] Ulyanov, Dmitry, Andrea Vedaldi, and Victor Lempitsky. "Instance normalization: The missing ingredient for fast stylization." arXiv preprint arXiv:1607.08022 (2016).

[10] Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).

[11] Touvron, Hugo, et al. "Llama 2: Open foundation and fine-tuned chat models." arXiv preprint arXiv:2307.09288 (2023).

[12] Groeneveld, Dirk, et al. "Olmo: Accelerating the science of language models." arXiv preprint arXiv:2402.00838 (2024).

[13] Shazeer, Noam. "Glu variants improve transformer." arXiv preprint arXiv:2002.05202 (2020).

[14] Almazrouei, Ebtesam, et al. "The falcon series of open language models." arXiv preprint arXiv:2311.16867 (2023).

[15] Google DeepMind (Gemma Team). “Gemma: Open Models Based on Gemini Research and Technology” (2024).

[16] He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.

[17] Jastrzębski, Stanisław, et al. "Residual connections encourage iterative inference." arXiv preprint arXiv:1710.04773 (2017).

[18] Veit, Andreas, Michael J. Wilber, and Serge Belongie. "Residual networks behave like ensembles of relatively shallow networks." Advances in neural information processing systems 29 (2016).

[19] Li, Hao, et al. "Visualizing the loss landscape of neural nets." Advances in neural information processing systems 31 (2018).

[20] Sennrich, Rico, Barry Haddow, and Alexandra Birch. "Neural machine translation of rare words with subword units." arXiv preprint arXiv:1508.07909 (2015).

[21] Kudo, Taku, and John Richardson. "Sentencepiece: A simple and language independent subword tokenizer and detokenizer for neural text processing." arXiv preprint arXiv:1808.06226 (2018).

[22] Wu, Yonghui, et al. "Google's neural machine translation system: Bridging the gap between human and machine translation." arXiv preprint arXiv:1609.08144 (2016).

[23] Su, Jianlin, et al. "Roformer: Enhanced transformer with rotary position embedding." arXiv preprint arXiv:2104.09864 (2021).

[24] Chowdhery, Aakanksha, et al. "Palm: Scaling language modeling with pathways." arXiv preprint arXiv:2204.02311 (2022).

[25] Dao, Tri, et al. "Flashattention: Fast and memory-efficient exact attention with io-awareness." Advances in Neural Information Processing Systems 35 (2022): 16344-16359.

[26] “Introducing MPT-7B: A New Standard for Open-Source, Commercially Usable Llms.” Databricks, 5 May 2023, https://www.databricks.com/blog/mpt-7b.

[27] Google Gemini Team et al. “Gemini: A Family of Highly Capable Multimodal Models”, https://storage.googleapis.com/deepmind-media/gemini/gemini_1_report.pdf (2023).

[28] Ainslie, Joshua, et al. "GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints." arXiv preprint arXiv:2305.13245 (2023).

[29] Zhang, Biao, and Rico Sennrich. "Root mean square layer normalization." Advances in Neural Information Processing Systems 32 (2019).

[30] Touvron, Hugo, et al. "Llama: Open and efficient foundation language models." arXiv preprint arXiv:2302.13971 (2023).

[31] Press, Ofir, Noah A. Smith, and Mike Lewis. "Train short, test long: Attention with linear biases enables input length extrapolation." arXiv preprint arXiv:2108.12409 (2021).

[32] Rafailov, Rafael, et al. "Direct preference optimization: Your language model is secretly a reward model." Advances in Neural Information Processing Systems 36 (2024).

[33] Ouyang, Long, et al. "Training language models to follow instructions with human feedback." Advances in Neural Information Processing Systems 35 (2022): 27730-27744.

[34] Ahmadian, Arash, et al. "Back to Basics: Revisiting REINFORCE Style Optimization for Learning from Human Feedback in LLMs." arXiv preprint arXiv:2402.14740 (2024).

Here, the // symbol indicates that we are performing integer division.

To perform dropout on attention scores, we just pass the attention matrix through a Dropout module in PyTorch.

Many different types of normalization exist; see here for more details. In deep learning, we typically use the standard score form of normalization, which transforms each value by subtracting the mean and dividing by the standard deviation

Notably, group [8] and instance [9] normalization are also widely-used normalization techniques. However, these normalization techniques are more commonly used for computer vision, so we avoid including them in the discussion here. See this article for a more comprehensive discussion.

This is typically done by taking an exponentially moving average of mean and standard deviation values that are observed for each mini-batch during training.

In fact, the original motivation for layer normalization was the simple fact that batch normalization did not work for recurrent neural networks! As is explained in [7], batch normalization struggles to handle small batch sizes and inputs that vary across time steps, such as for recurrent neural networks. For these cases, normalizing each input independently (via layer normalization) works much better.

The word “pointwise” indicates that the same operation is applied to every token vector in the sequence. In this case, we individually pass every token vector in the sequence through the same feed-forward neural network with the same weights.

As explained in the NanoGPT repository and a few related publications [11, 12], excluding bias (for both linear/feed-forward layers and layer normalization) actually makes LLMs slightly better, faster, and more stable!

We can also apply residual connections to layers that have differently-sized inputs and outputs. To do this, we just have to add an extra linear projection that transforms the shape of the input to match that of the output.

For those who are not familiar with computing gradients in a neural network via backpropagation, check out this awesome book chapter.

In fact, the first project I worked on involving (BERT-style) language models was nearly a failure! After a few weeks of trying to debug the model’s performance, I fixed most of the issues I was facing by training a custom tokenizer over my own data.

For masked self-attention, this is not 100% accurate, as the position of the token in the sequence may change which tokens are masked or not masked.

There are numerous different ways that we can perform this sampling at inference time; e.g., greedy selection, modifying the temperature, nucleus sampling, top-K sampling, and more. See here for a great overview of decoding techniques.

In particular, the parallel block reduces the communication costs of tensor parallel training by reducing the required number of all_reduce operations from two to one within each transformer block.

See the CausalSelfAttention implementation in this file for an example invocation of FlashAttention in PyTorch.

See here for an implementation of RoPE embeddings within PaLM.

Sam

Mar 5, 2024

A question that I have at the end -- if ALiBi indeed "outperforms" both RoPE and vanilla positional embedding techniques (with respect to extrapolating to longer sequences), why was it "only" (*) used for MPT, rather than for recent models like LLaMA-2, which used RoPE?

I'd like to better understand (maybe a different post, maybe even one you've done) the dimensions across which I'd compare different attention variants.

3 replies by Cameron R. Wolfe, Ph.D. and others

Sahana

May 17

This is one of the best article I have seen on the topic. This is exactly the one I wanted to understand practical implementation. Thank you so much for taking the time.

14 more comments...

Deep (Learning) Focus

Discussion about this post

Ready for more?