Mixture-of-Experts (MoE): The Birth and Rise of Conditional Computation
What two decades of research taught us about sparse language models...
Modern advancements in large language models (LLMs) are mostly a product of scaling laws [6]. As we increase the size of the underlying model, we see a smooth increase in performance, assuming that the model is trained over a sufficiently large dataset [7]. Such scaling laws eventually led us to the creation of GPT-3, as well as other (more powerful) LLMs that followed it. When scaling up these dense LLMs, we will eventually reach a hardware-imposed limit due to heightened memory costs and the dependence of the model’s compute footprint on the total number of parameters. As a result, compute and data have become the primary bottleneck for training better LLMs—creating a better model is relatively simple given access to more compute and data. In this overview, we will study how this limitation can be avoided by training sparsely activated language models.
“As the training of giant dense models hits the boundary on the availability and capability of the hardware resources today, Mixture-of-Experts (MoE) models have become one of the most promising model architectures due to their significant training cost reduction compared to quality equivalent dense models.” - from [12]
Mixture-of-Experts (MoE) layers are simple and allow us to increase the size or capacity of a language model without a corresponding increase in compute. We just replace certain layers of the model with multiple copies of the layer—called “experts”—that have their own parameters. Then, we can use a gating mechanism to (sparsely) select the experts used to process each input. This idea has its roots in research on conditional computation in the early 1990s [15, 30] and allows us to train massive models in a tractable manner, which is helpful in domains—such as language modeling—that benefit from models with extra capacity. Here, we will study the MoE, its origins, and how it has evolved over the last two decades.
TL;DR: What is a Mixture of Experts (MoE)?
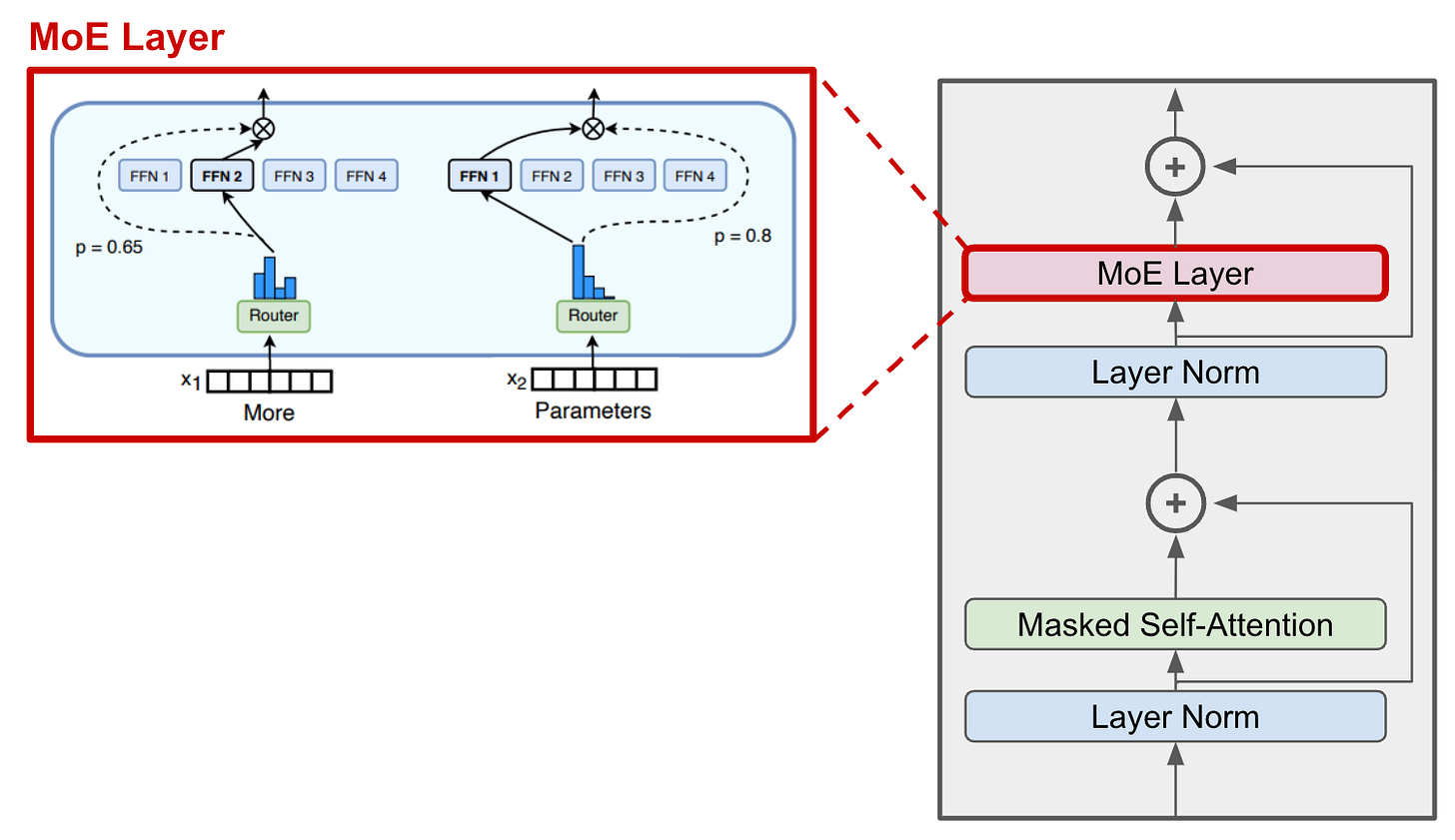
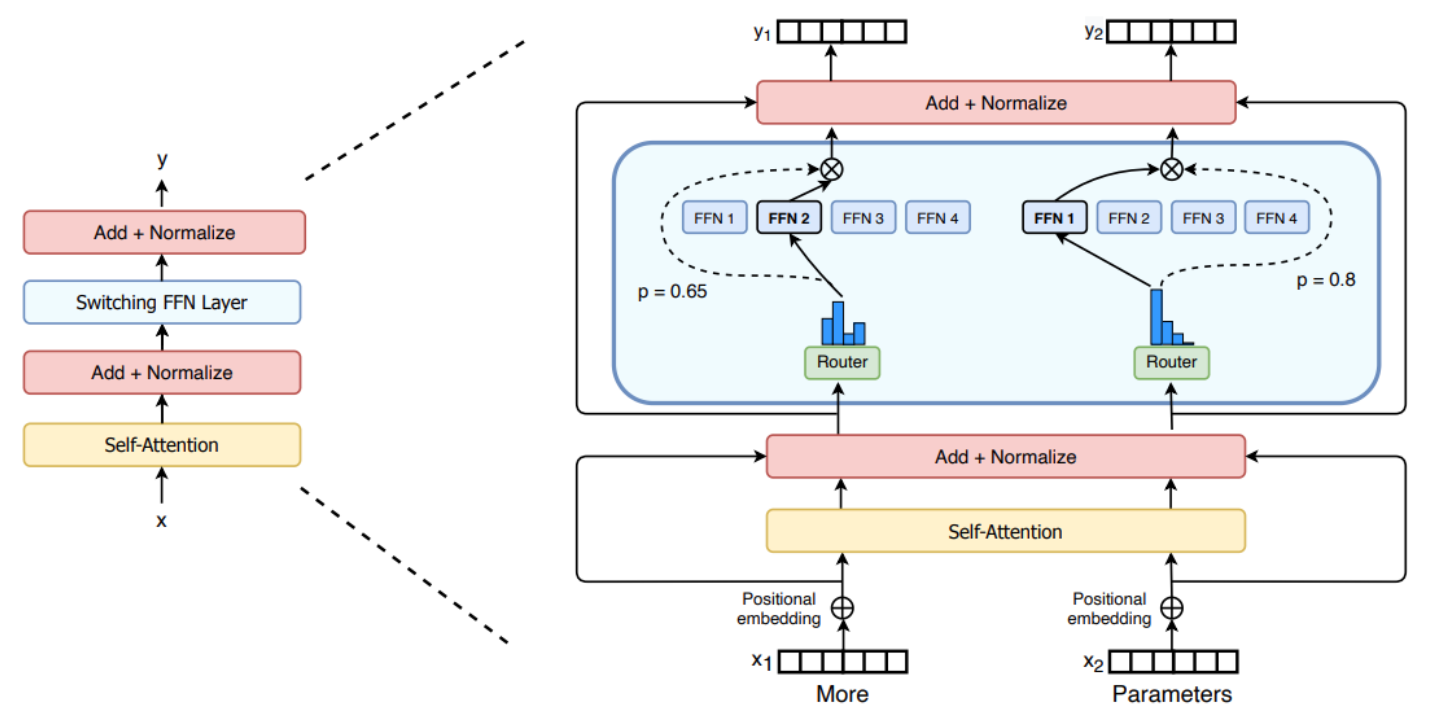
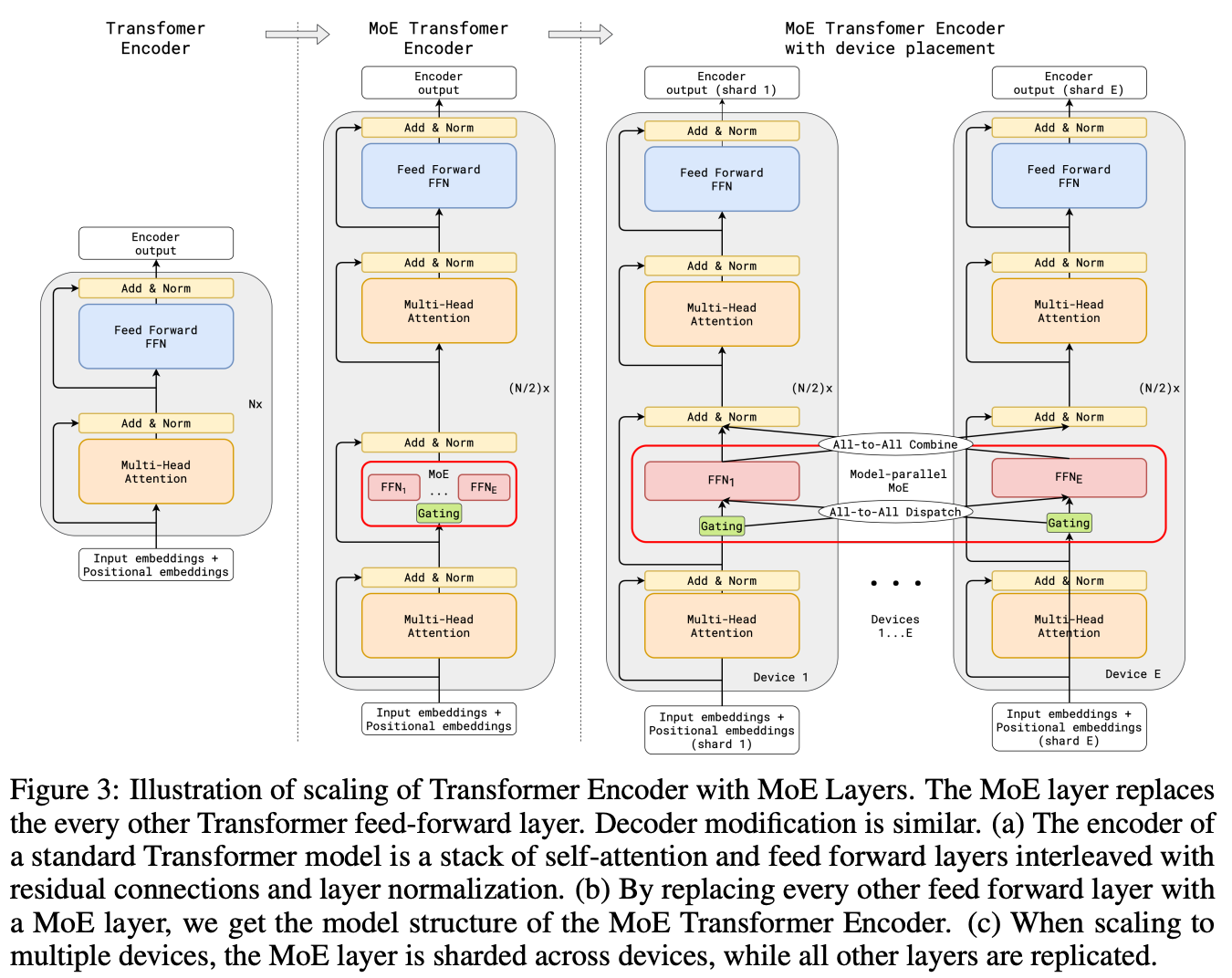
The standard decoder-only transformer architecture used by most generative LLMs is shown in the figure above; see here for an in-depth overview of this architecture. In the context of LLMs, MoEs make a simple modification to this architecture—we replace the feed-forward sub-layer with an MoE layer! This MoE layer is comprised of several experts (i.e., anywhere from a few experts [13] to thousands [5]), where each expert is its own feed-forward sub-layer with an independent set of parameters; see below for a depiction.
We can similarly convert encoder-decoder transformers, such as T5 [8], into MoE models by replacing feed-forward sub-layers in both the encoder and the decoder with MoE layers. However, we usually only convert a portion of these sub-layers (e.g., every other layer) to MoE layers. In this overview, we will primarily overview work with MoE models based upon the encoder-decoder transformer, while work on MoE-based autoregressive LLMS will be covered in a future post.
“The ST-MoE models have 32 experts with an expert layer frequency of 1/4 (every fourth FFN layer is replaced by an MoE layer).” - from [24]
Sparse experts. This approach might seem problematic because it adds a ton of parameters to the model. The MoE model has multiple independent neural networks (i.e., instead of a single feed-forward neural network) within each feed-forward sub-layer of the transformer. However, we only use a small portion of each MoE layer’s experts in the forward pass! Given a list of tokens as input, we use a routing mechanism to sparsely select a set of experts to which each token will be sent. For this reason, the computational cost of an MoE model’s forward pass is much less than that of a dense model with the same number of parameters.
Components of an MoE layer. When applied to transformer models, MoE layers have two primary components:
Sparse MoE Layer: replaces dense feed-forward layers in the transformer with a sparse layer of several, similarly-structured “experts”.
Router: determines which tokens in the MoE layer are sent to which experts.
Each expert in the sparse MoE layer is just a feed-forward neural network with its own independent set of parameters1. The architecture of each expert mimics the feed-forward sub-layer used in the standard transformer architecture. The router takes each token as input and produces a probability distribution over experts that determines to which expert each token is sent; see below.
The router has its own set of parameters and is trained jointly with the rest of the network. Each token can be sent to many experts, but we impose sparsity by only sending a token to its top-K experts. For example, many models set k=1 or k=2, meaning that each token is processed by either one or two experts, respectively.
Greater capacity, fixed computation. Increasing the size and capacity of a language model is one of the primary avenues of improving performance, assuming that we have access to a sufficiently large training dataset. However, the cost of training increases with the size of the underlying model, which makes larger models burdensome in practice. MoE models avoid this expense by only using a subset of the model’s parameters during inference.
“Assuming just two experts are being used per token, the inference speed is like using a 12B model (as opposed to a 14B model), because it computes 2x7B matrix multiplications, but with some layers shared” - from HuggingFace MoE blog
For example, assume we have a 7B parameter LLM and replace each of its feed-forward sub-layers with an MoE layer comprised of eight experts, where two experts are activated for each token. This is the exact architecture that was used for Mixtral-8x7B [13], an MoE variant of Mistral-7B [14]. The full model has about 47B parameters2, all of which must be loaded into memory. But, the model’s inference cost is comparable to a 14B parameter model. Only two experts are used to process each token, which yields ~2 x 7B matrix multiplications3. In this way, we achieve the capacity of a ~50B parameter model without incurring the cost!
Pros and cons. MoE models are widely used due to their ability to train larger models with a fixed compute budget, but using an MoE-style LLM has both pros and cons! MoE models pretrain faster compared to dense models, as well as have much faster inference compared to a dense model with the same number of parameters. MoEs allow us to increase model capacity while keeping the amount of compute that we use (relatively) low. However, MoE-style LLMs also consume more VRAM, as all experts must be loaded into memory. Additionally, MoE models are prone to overfitting and notoriously difficult to finetune, which makes them more complicated to use in practical applications compared to dense models.
Origins of the Mixture-of-Experts
Although MoEs are very popular in recent AI research, the idea has been around for a long time. In fact, the concept of conditional computation—or dynamically turning parts of a neural network on/off—has its roots in work from the early 1990s! In this section, we will explore this early work on conditional computation and study how it has evolved to form the idea of an MoE. Eventually, these ideas were applied (with some success) to training early, LSTM-based [4] language models.
Early Work on Conditional Computation
“Conditional computation, where parts of the network are active on a per-example basis, has been proposed in theory as a way of dramatically increasing model capacity without a proportional increase in computation” - from [1]
The idea of an MoE has its origins in work done by Geoffrey Hinton in the early 1990’s [15], which proposes a supervised learning framework for an ensemble of several networks. Each of these networks is expected to process a different subset of the training data, and the choice of which network to use is handled by a gating mechanism; see below. In other words, each network in this system is an expert that specializes in processing some domain (or region) of the input data.
Since the proposal of [15], several works have explored and extended this idea of conditional computation. For example, authors in [30] (also written in the early 1990s!) propose a hierarchical (tree-structured) MoE that can be trained in a supervised fashion using an expectation-maximization algorithm; see below. There are many such works that study this topic in-depth.
Estimating or propagating gradients through stochastic neurons for conditional computation [16]. This work explores four possible techniques for estimating the gradient of stochastic neurons and hard-threshold activation functions; e.g., by using REINFORCE, a straight-through estimator, or additive/multiplicative noise. Although these terms might seem unfamiliar, conditional computation is one example of a hard-threshold activation function—the activations of certain neurons are completely eliminated (or set to zero) from the computation. The estimators that are proposed in [16] are necessary for training networks that use conditional computation. The neural network structure explored in [16] is comprised of many computational units connected by a distributed network of gates that can be used to eliminate chunks of computation. By turning off portions of this network, we can greatly reduce the computational cost of a large neural network.
Low-rank approximations for conditional feedforward computation in deep neural networks [17]. This work explores a neural network setup in which the nodes of the network are supplemented with gating units that determine whether a node should be calculated or not; see above. Because ReLU sets all negative activation values to zero within a neural network, any node with a negative pre-activation value can be removed from the computation altogether. Expanding upon this idea, authors show in [17] that the sign of hidden activations prior to ReLU can be estimated by computing a low-rank approximation of the weight matrix, resulting in significant efficiency gains when the network is sparse.
Learning factored representations in a deep mixture of experts [18]. This work considers MoE layers comprised of several expert networks that specialize in processing different regions of the input space. Inputs are mapped to these experts using a learned gating mechanism, allowing larger networks to be computed sparsely. Going further, authors in [18] consider deeper networks with multiple, consecutive MoE layers (i.e., a “stacked” MoE), as shown in the figure above. When testing these networks on the MNIST dataset, we see that the Deep MoE learns unique features at each layer; e.g., the first layer learns location-dependent features, while the second layer learns class-specific features.
“Conditional computation has been proposed as a way to increase the capacity of a deep neural network without increasing the amount of computation required, by activating some parameters on-demand, on a per-example basis.” - from [19]
Exponentially increasing the capacity-to-computation ratio for conditional computation in deep learning [19]. Larger models are widely known to perform better4. If the amount of computation was not an issue, we could use larger datasets and models to yield improved generalization, but the amount of computation used by a deep network increases with the parameter count. To avoid this issue and better leverage conditional computation, authors in [19] propose a novel weight matrix parameterization that turns off groups of parameters when specific patterns of hidden activations are observed5. Such an approach can exponentially increase the ratio of parameters to computation.
Conditional computation in neural networks for faster models [20]. This work explores reinforcement learning-based training strategies (i.e., REINFORCE) for neural networks that use conditional computation. We see that this approach, which uses policy gradient algorithms, can be used to train networks in a way that maintains accuracy while maximizing computation speed. Plus, we can use regularization to diversify the patterns of conditional computation observed in the networks. In experiments, this learning strategy is shown to yield networks that achieve a favorable balance between compute cost and performance.
Dynamic Capacity Networks (DCNs) [21] adaptively assign capacity to different portions of the input data by defining low-capacity and high-capacity sub-networks. For most of the data, low-capacity sub-networks are applied. However, a gradient-based attention mechanism can be used to select portions of the input—based upon the network’s sensitivity to this region of the data—to which high-capacity sub-networks will be applied; see above. We see in experiments that DCNs can reduce computation while achieving performance that is comparable to (or better than) that of traditional convolutional neural networks (CNNs).
Deep sequential neural networks [22] discards the traditional notion of a “layer” used within neural network architectures, choosing instead to construct an entire set of candidate transformations that can be selectively applied at each layer. When processing an input, one element from the candidate set is chosen at each layer, forming a DAG-like architecture based upon a sequence of transformations. Depending upon properties of the input data, the selected sequence of transformations may vary, which increases the expression power of the model compared to classical multi-layer networks. Similar to prior work, this sequential architecture is trained using a policy gradient approach.
Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer [1]
“We obtain greater than 1000x improvements in model capacity with only minor losses in computational efficiency and significantly advance the state-of-the-art results on public language modeling and translation data sets.” - from [1]
The idea of conditional computation holds an incredible amount of promise. Especially in the domain of language modeling where training datasets tend to be massive6, the ability to increase the model’s underlying capacity without causing a corresponding increase in computation is enticing to say the least. Despite being studied for over two decades, MoEs fell short of their promise due to various technical challenges. In [1], authors attempt to overcome some of these challenges with the proposal of the Sparsely-Gated Mixture-Of-Experts layer, showing that MoEs can be applied to language modeling and translation domains.
Prior issues with MoEs. Although work in [1] was one of the first to apply MoEs to language modeling, the idea of an MoE dates back to the early 1990s. With this in mind, we might wonder: What prevented MoEs from being more widely adopted? Several technical roadblocks contributed to this lack of adoption:
GPUs are great at performing arithmetic efficiently, but they are not as good at branching (i.e., a major component of conditional computation).
Large batch sizes are needed to train neural networks efficiently, but MoEs reduce batch sizes (i.e., each expert only receives a portion of the input batch).
Increased model capacity is most impactful when studying domains with larger training datasets, and MoEs were largely studied in computer vision domains on problems with insufficiently-large training datasets.
What is a Sparse MoE? The style of MoE layers used by most modern LLMs is similar to the sparsely-gated mixture-of-experts layer proposed in [1] (depicted above), which is a generic neural network module with two components:
Experts: each layer has several “experts” that are standalone neural network modules or layers with independent sets of parameters.
Router: a parametric (and learnable) gating mechanism that selects a (sparse) group of experts used to process each input.
In [1], each expert within an MoE is a feed-forward neural network with an identical architecture. However, more complex architectures could be used; e.g., we can even create “hierarchical” MoE modules by implementing each expert as another MoE! Both the experts and the gating mechanism are jointly trained along with other network parameters via gradient descent.
To compute the output of an MoE module, we take a weighted combination of expert outputs, where weights are provided by the router; see above. The router outputs a N-dimensional vector of weights (i.e., N is the number of experts). Although this approach might not initially seem useful, the magic happens when the router’s output is sparse—experts that receive a weight of zero are no longer considered when computing the output of an MoE. For this reason, MoEs allow us to create, train and use very large neural networks without significant compute requirements, as only a portion of model parameters are used at any given time.
Gating mechanism. Many different strategies have been proposed for routing within an MoE. The simplest approach would be to multiply our input by a weight matrix and apply softmax; see above. However, this approach does not guarantee that the selection of experts will be sparse7. To solve this issue, authors in [1] propose a modified gating mechanism that adds sparsity and noise to this simplistic softmax gating mechanism; see below.
The gating mechanism above performs routing similarly to the softmax gating mechanism, but we include two additional steps:
An adjustable amount of Gaussian noise is added to the output of the router prior to applying softmax.
All but the output of the top-
Kexperts are masked (i.e., set to -∞) to ensure that the selection of experts is sparse.
Balancing the experts. One issue with MoEs is that the network has a tendency to repeatedly utilize the same few experts during training. Instead of learning to use all experts uniformly, the gating mechanism will converge to a state that always selects the same set of experts for every input. This is a self-fulfilling loop—if one expert is selected most frequently, it will be trained more rapidly and, therefore, continue to be selected over the other experts! Prior work has proposed several approaches for solving this issue [2, 3], but we see in [1] that experts can be balanced by adding a simple “soft” constraint to the training loss; see below.
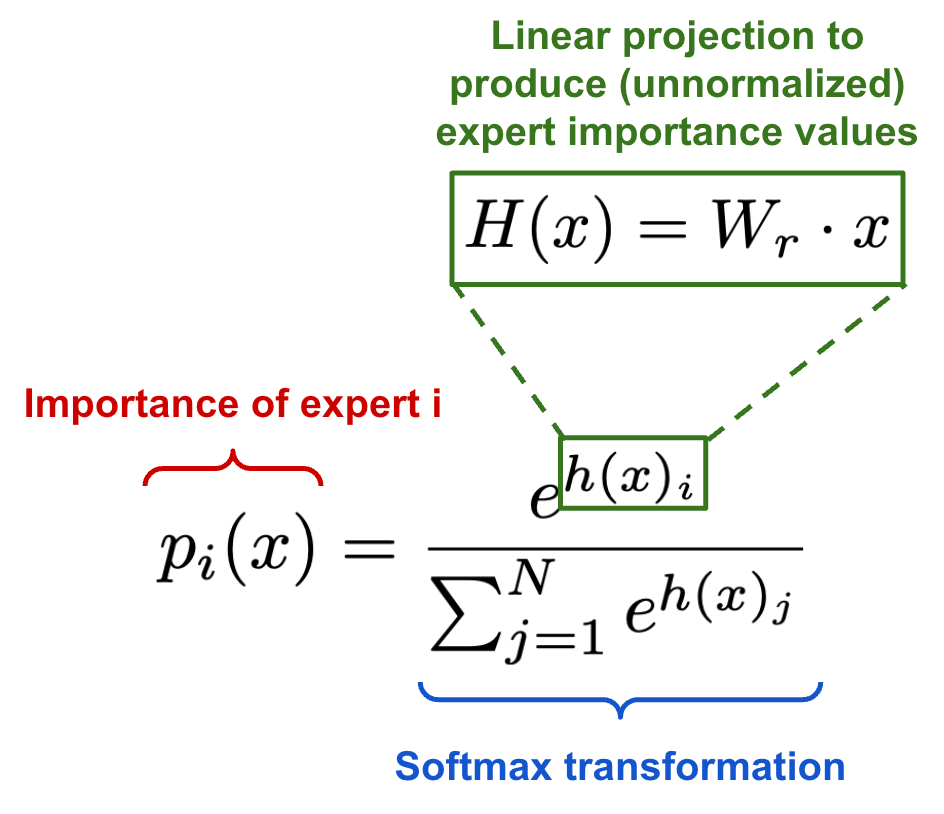
We first define an “importance” score for each expert over a batch of input data, which can be computed by taking a sum over the gate values for each expert across the batch. Put simply, experts that are selected frequently in the batch will have a high importance score. Then, we can compute an auxiliary loss function by taking the squared coefficient of variation (CV) of expert importance scores; see above. If experts all have very similar importance scores, the CV will be small and vice versa. This loss term can be added to the model’s training objective to encourage experts to receive equal importance within each batch.
Empirical evaluation. To test the performance of their sparse MoE layer, authors in [1] train a language model that inserts an MoE module between stacked layers of an LSTM8. The MoE module is applied convolutionally, meaning that several LSTM time steps are processed at once (in batch). Additionally, a new distributed training strategy is proposed that combines model and data parallel training to eliminate issues with shrinking batch sizes in the MoE. Such a strategy, along with some other system optimizations, allows language models with as many as 137B parameters to be trained with reasonable compute requirements!
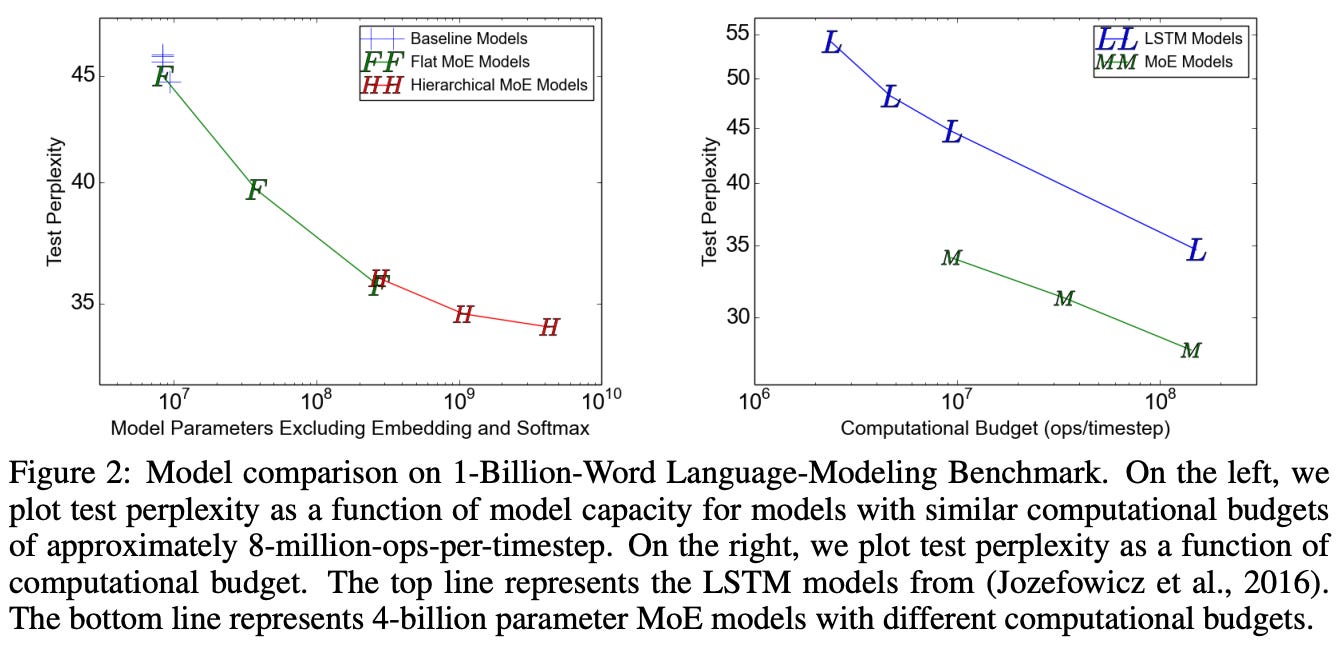
These models are evaluated on language modeling datasets of varying sizes (i.e., 1, 10, and 100 billion words). Both flat and hierarchical MoEs are tested with varying numbers of experts, and all models are trained such that their total computational cost is roughly equal (i.e., the number of active experts k is the same)9. Even when studying the smallest dataset, we see that the largest of the MoE models yields a noticeable improvement in perplexity (lower is better); see above.
If the size of the training dataset is sufficiently small, then adding more capacity via more experts has diminishing returns, as shown above. However, we see on larger datasets that performance continues to improve up to a size of 68B parameters (i.e., 65,536 experts)! Such a finding emphasizes the synergy between MoE layers and the language modeling domain—added model capacity is helpful given a sufficiently large training corpus. Work in [1] showed for the first time that these benefits could be achieved in practice without noticeably increasing compute costs, setting the stage for MoEs to become a popular tool for LLMs.
“The widening gap between the two lines demonstrates (unsurprisingly) that increased model capacity helps more on larger training sets.” - from [1]
Applying Mixture-of-Experts to Transformers
Now that we have studied early work on conditional computation, we can take a look at some applications of MoEs to the transformer architecture. Today, MoE-based LLM architectures (e.g., Mixtral [13] or Grok) have become popular, but MoEs were explored for language models in several stages. Here, we will take a look at applying MoEs to the encoder-decoder transformer architecture. This work is relevant to modern LLM applications and derives countless lessons for using MoEs effectively in practice. Such research sets the stage for later work that explores MoE-based generative LLMs, which will be covered in a future overview.
Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity [5]
After the proposal of the sparsely-gated MoE in [1], work on transformers and language models had yet to begin using these ideas—adoption was hindered by the general complexity of MoEs, as well as issues like high communication costs and training instability. Aiming to solve these issues, authors in [5] propose an MoE-based encoder-decoder transformer architecture, called the Switch Transformer, that uses a simplified gating mechanism to make training more stable, thus making MoEs a more realistic and practical choice for language modeling applications.
“Simple architectures— backed by a generous computational budget, data set size and parameter count—surpass more complicated algorithms” - from [5]
When the Switch Transformer was proposed, researchers were just beginning to study neural scaling laws [6], which show that a language model’s performance smoothly improves as we increase its size10. With this in mind, work in [5] is motivated by the fact that MoE models allow us to add another dimension to the analysis of neural scaling laws—we can increase model size while keeping the computational complexity of the model’s forward pass constant.
Applying MoE to transformers. To create an MoE variant of an encoder-decoder transformer, we can simply convert the feed-forward sub-layers of the model into MoE layers; see above. The feed-forward transformation is applied in a pointwise fashion, meaning that each token is passed individually through the feed-forward network. For this reason, each token within the sequence is individually routed to its set of corresponding experts. For example, each token in the sequence [“I”, “love”, “LLM”, “#s”] is passed through the routing function, forming a probability distribution over experts. Then, we select the top-K experts for each individual token—tokens in the same sequence are not always sent to the same experts.
Better routing. In prior work, the minimum number of active experts in any MoE layer was two. Using at least two experts was thought to be necessary to have non-trivial gradients in the routing function11. In [5], authors propose routing each token to only a single expert—this is called a switch layer. By routing to a single expert, we simplify the routing function, reduce computational overhead, and lessen communication costs while improving the model’s performance.
The routing function used by the Switch Transformer (shown above) is just a softmax gating mechanism. We pass each token vector through a linear layer that produces an output of size N (i.e., the number of experts), then apply a softmax transformation to convert this output into a probability distribution over experts.
From here, we compute the output of the switch layer by i) selecting a single expert and ii) scaling the output of this expert by the probability assigned to that expert by the routing function; see above. Notably, this approach differs from [1] because it computes a distribution over all experts, rather than only considering the distribution over top-K experts. In other words, we still compute a probability distribution over all N experts in the routing function, then compute the layer’s output by scaling the output of the selected expert by its probability; see above. This approach allows us to train the MoE model even when K=1.
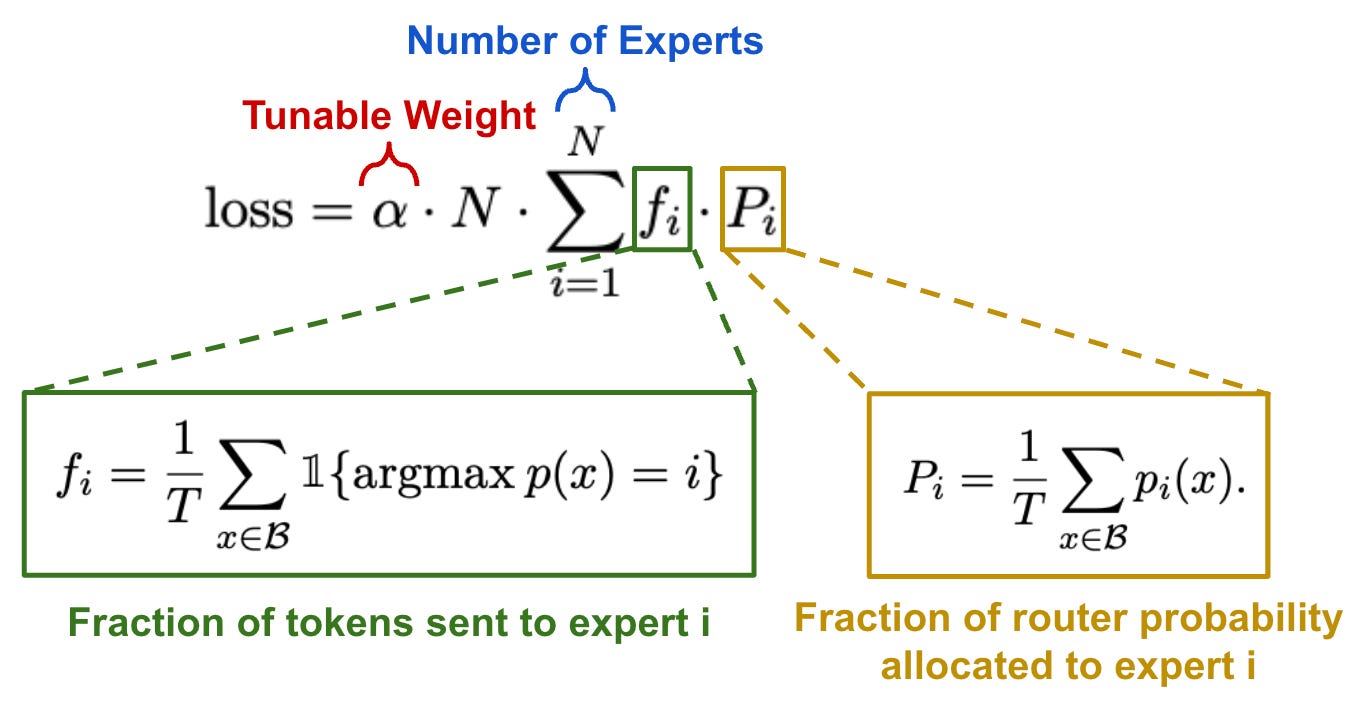
Simple load balancing. In [1], authors employ multiple auxiliary loss functions to balance importance scores and perform load balancing between experts (i.e., meaning that each expert is sent a roughly equal number of tokens from the batch). We see in [5] that both of these objectives can be achieved with a single auxiliary loss function that is applied at each switch layer in the model; see below.
This loss, which is differentiable with respect to P and can be easily incorporated into training, encourages both the fraction of tokens allocated to each expert and the fraction of router probability allocated to each expert to be 1/N, meaning that experts are equally important and receive a balanced number of tokens.
Capacity factor. Within the Switch Transformer, we set a global “expert capacity” variable that determines the maximum number of tokens that can be routed to each expert in any MoE layer. The equation for expert capacity is shown below.
In a switch layer, each token is routed to the expert that is assigned the highest probability by the routing mechanism. If too many tokens (i.e., exceeding the expert capacity) are sent to a single expert, computation for these tokens will be skipped. These “dropped” tokens are passed directly to the next layer via the residual connection. Setting the capacity factor greater than one allows the MoE to handle cases where tokens are not perfectly balanced across experts; see below.
The expert capacity must be tuned to avoid having too many dropped tokens—the load balancing loss can also help with this by evenly routing tokens to experts—while not wasting computation or memory. Beyond the Switch Transformer, the capacity factor is an important hyperparameter for any MoE model that we can tune to improve hardware utilization by balancing computation across experts.
Practical evaluation. Authors in [5] evaluate a Switch Transformer model based upon T5 [8]. The model is pretrained on C4 using a masked language modeling (MLM) objective and a mixed precision strategy that uses bfloat16 format for certain operations. By only using low precision on select operations (e.g., the routing function is chosen to be performed in full precision), we can improve efficiency without causing training instabilities. Interestingly, authors note that they increase the dropout rate on MoE layers to avoid overfitting.
“The guiding principle for Switch Transformers is to maximize the parameter count of a Transformer model in a simple and computationally efficient way.” - from [5]
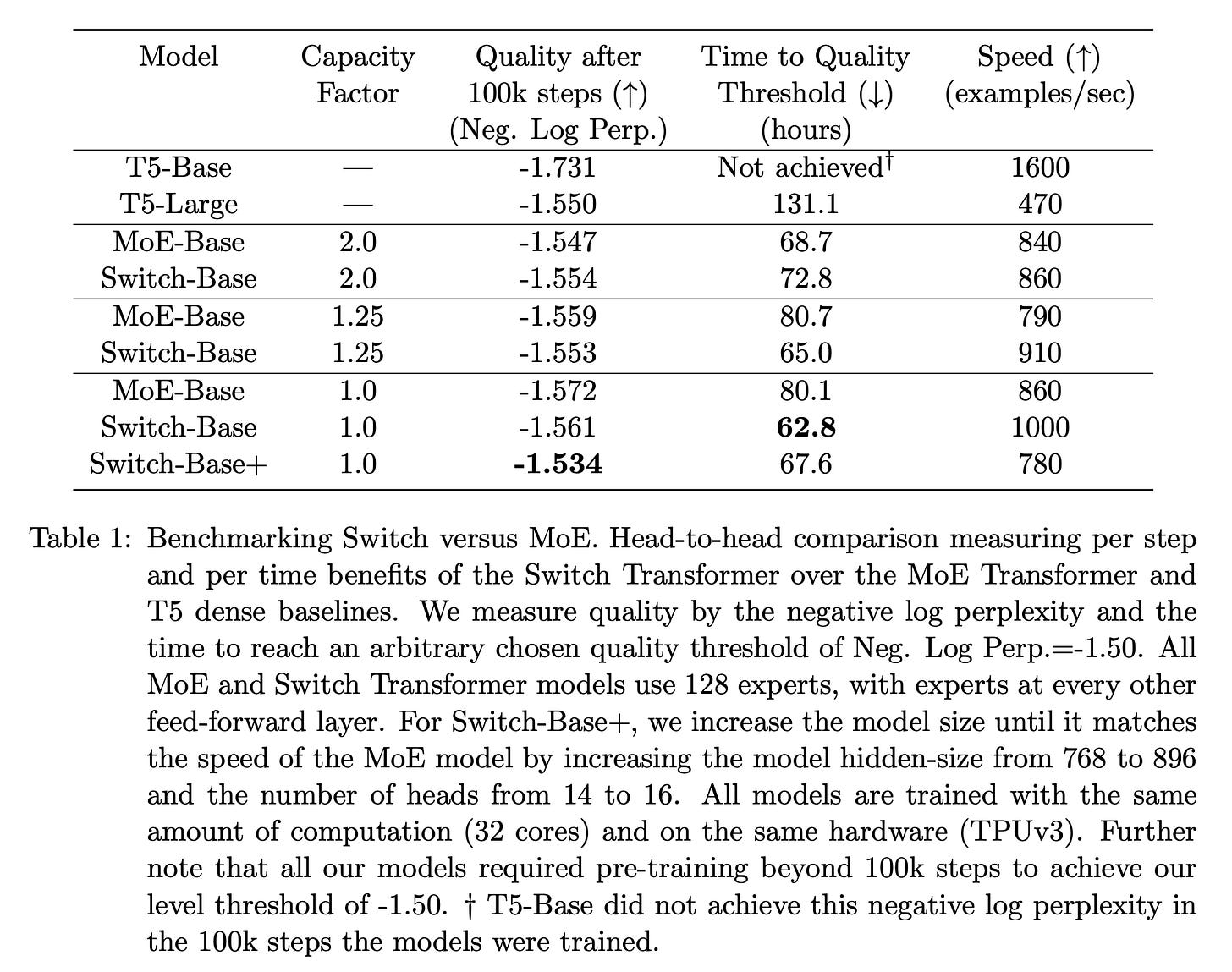
Using this approach, Switch Transformer models with up to 1.6T parameters are trained. To create these models, we start with a T5 architecture, convert each feed-forward sub-layer into an MoE, and increase the number of experts within each MoE layer! Despite the size of these models, the amount of compute spent on each token does not change much. In fact, training the Switch Transformer is up to 7X faster than training the base T5 model in certain cases. The MoE model has better statistical learning efficiency12 compared to T5 and performs better given a fixed amount of computation or time for training; see below.
Compared to standard MoE models [1], the Switch Transformer has a smaller compute footprint—due to having fewer active experts—and achieves better performance on a speed-quality basis. In other words, the Switch Transformer outperforms a comparable MoE model that is trained using the same amount of compute or for the same amount of time. We also see above that the Switch Transformer performs better at lower capacity factors compared to MoE, which allows us to improve training efficiency via better load balancing between experts.
Scaling properties. The results in [5] show us that MoE models—and the Switch Transformer variant in particular—benefit language modeling applications. Why have MoEs become so popular for language modeling? The simple reason is that MoE models allow us to scale up the size of the model at a stable computational cost. As shown in the figure above, LLM performance consistently improves as the number of experts is increased, producing scaling trends comparable to those observed for dense models. MoE models allow us to get the performance of a larger model while maintaining reasonable training and inference costs.
ST-MoE: Designing Stable and Transferable Sparse Expert Models [24]
Although it made MoE models more practical/usable, the Switch Transformer still had several issues. The model suffered from training instability, and authors in [5] show that the Switch Transformer—despite achieving pretraining speedups over dense models—lags behind the performance of prior state-of-the-art models when finetuned on popular benchmarks like SuperGLUE. Put simply, these MoE-based language models only perform well when the dataset is very large, otherwise their performance deteriorates due to overfitting. In [24], authors study the instability and finetuning difficulties of MoE models in-depth, providing a design guide (summarized above) for practical and reliable training of sparse models. Using this guide, authors train a sparse 269B parameter encoder-decoder model that is the first MoE-based model to achieve state-of-the-art transfer learning13 results.
Addressing training instability. Despite the benefits of sparse MoE models, they are much more prone to instabilities during training; see above. In [24], authors consider several techniques for mitigating this training instability and compare them based upon i) the performance of the model and ii) the ratio of training runs that are stable. Several techniques are found to improve stability at the cost of deteriorated model performance, such as:
Injecting noise into the model via dropout or input jitter (i.e., multiplying the router’s logits by a random value in the range
[0.99, 1.01]).Clipping gradients or weight updates based on a fixed threshold to remedy exploding gradients during backpropagation.
Removing components with multiplicative interactions (e.g., GeGLU activation [27] or the scaling factor in RMSNorm [28]) from the architecture.
We learn in [24] that constraining the values of the router’s logits (i.e., the output values of the router prior to softmax being applied) has the biggest impact on training stability. In prior work [5], we have seen that the routing mechanism cannot be computed in low precision because MoE models are sensitive to roundoff errors. Due to the exponential in the routing function (shown below), such roundoff errors can occur in the router and lead to training instabilities.
For this reason, router logits that are too large could negatively impact training stability. However, simply clipping (i.e., applying a hard threshold to remove large values) router logits can damage model performance. Instead, the router z-loss (formulated below) is proposed in [25] as an auxiliary loss that encourages smaller values (and fewer roundoff errors) within the routing mechanism.
This loss just penalizes large logits within the gating mechanism of the MoE. To incorporate the router z-loss into the training process of the MoE model, we can simply combine it with the normal training loss and the auxiliary load balancing loss (see below), where we weight each of these losses according to their relative importance. The router z-loss significantly improves training stability without causing any noticeable deterioration in model quality.
Debugging finetuning issues. Although sparse models perform well with large datasets, we’ve seen that finetuning these models can be difficult. In [24], authors confirm that these finetuning ailments are due to overfitting by studying the performance of pretrained sparse and dense models on downstream tasks with both small (CommitmentBank) and large (ReCoRD) training datasets14. In these experiments, we see that the sparse model converges more quickly than the dense model in both cases. However, the validation quality of the sparse model is much worse than that of the dense model on the downstream task with less data. In other words, the sparse model overfits due to a lack of sufficient data; see below.
To mitigate overfitting, authors first attempt to only finetune certain portions of the MoE model’s parameters. Interestingly, finetuning just the MoE layers yields a drastic deterioration in performance, while selectively finetuning other groups of parameters performs comparably to finetuning all parameters; see below.
Going further, we see that sparse and dense models tend to require different hyperparameter settings for effective finetuning. In particular, MoE models benefit from high learning rates and smaller batch sizes, both of which improve generalization by introducing more noise to the training process. Additionally, we see that the capacity factor does not drastically impact finetuning results. In fact, we can remove the auxiliary load balancing loss during finetuning without any issues—sparse models are robust to dropping up to 10-15% of tokens; see below.
However, there is no definitive solution provided in [24] that solves the difficulty of finetuning MoE models. Authors confirm that these issues arise due to overfitting and analyze different choices that help to combat overfitting. However, even the optimally-designed models analyzed in the experimental section of [24] continue to overfit on smaller downstream tasks! Improved forms of regularization for finetuning MoEs are still an active area of research.
Optimal MoE design. Based on their extensive analysis, authors in [24] outline high-level takeaways (shown above) for effectively designing and using MoE models15. This analysis focuses primarily upon choosing the correct capacity factor and number of experts within the MoE. Put simply, we see in [24] that the optimal setup for an MoE model is hardware-dependent. For example, authors recommend using at most one expert per TPU/GPU core and note that optimal values for the capacity factor and number of experts are hardware-dependent. Changes to the capacity factor—due to scaling up the maximum number of tokens sent to each expert—have several downstream effects:
Higher memory requirements for activations.
Heightened communication costs.
Increased computation in each expert’s forward pass.
On the flip side, higher capacity factors can improve model quality! For a system with fast interconnects and powerful GPUs, the spike in computation and communication costs might be worth it. However, the choice of MoE parameters is a tradeoff that depends heavily upon the available hardware.
Practical takeaway. Authors in [24] conclude their work by using the lessons outlined above to train a 269B parameter encoder-decoder transformer model—with the same compute complexity as a 32B parameter dense model—based upon T5-Large [8]. Compared to prior MoE models, the ST-MoE-32B model has fewer parameters and a higher computational complexity. There are fewer, but larger, experts in each MoE layer. Previously, such high-FLOP MoEs were found to be unstable during training, but the addition of the router z-loss enables the ST-MoE-32B model to be trained successfully. Because it has fewer parameters compared to prior MoE models, ST-MoE-32B is easier to finetune and deploy.
“We sought a balance between FLOPs and parameters. High-FLOP sparse models were previously unstable in our setting (i.e. encoder-decoder models, Adafactor optimizer), but the router z-loss enabled us to proceed.” - from [24]
The model is pretrained on 1.5 trillion tokens of data from a combination of C4 and the dataset used to train GLaM [25]. Afterwards, finetuning is performed over a mixture of all downstream tasks—where each task is sampled proportionally according to its training set size16—prior to evaluation. The results of this model are displayed below, where we see that it sets new state-of-the-art performance across a wide range of NLP tasks. Notably, ST-MoE-32B is the first sparse model to achieve state-of-the-art results in the transfer learning domain, as prior models struggled heavily with overfitting during the finetuning process.
Other Notable MoE Papers
Prior to the popularization of MoE-style LLMs, many papers were written on this topic beyond the research we explored in [5] and [24]. Some notable publications in this area are outlined below to provide a more comprehensive picture of research that has been conducted on MoEs in the language modeling domain.
GShard [9] proposes a framework and set of tools for easily implementing parallel computation patterns in neural networks, such as a Sparsely-Gated MoE layer. This framework is then used to scale a transformer-based neural machine translation model to a size of over 600B parameters. Using GShard, this model can be efficiently trained on over 2048 TPUs in 4 days and surpasses the quality of prior models on translating over 100 different languages to English. Some useful takeaways for effectively training MoE models in GShard include:
Every other feed-forward sub-layer in the encoder-decoder transformer is replaced with an MoE layer.
Top-2 routing is used in both the encoder and the decoder.
The routing mechanism always picks the top expert, but the second expert is randomly chosen with probability proportional to its weight.
“Where data-parallelism can be viewed as splitting tensors and operations along the batch dimension, in Mesh-TensorFlow, the user can specify any tensor-dimensions to be split across any dimensions of a multi-dimensional mesh of processors.” - from [31]
Mesh-Tensorflow [31] greatly simplified the exploration of efficient, model-parallel distributed training strategies, which split the model itself across multiple devices (i.e., GPUs or TPUS)17, for neural networks. Previously, data parallel strategies, which split the input batch of data across multiple devices, were the dominant approach for distributed training of neural networks, but data parallel training has several downsides; e.g., training large models is harder because each device must keep a full copy of the model in memory and efficiency deteriorates with small batch sizes. Put simply, Mesh-Tensorflow is just a general language that can be used to specify distributed computations. After the release of this tool, MoE layers were re-introduced into the transformer architecture, as programming data-parallel and model-parallel training strategies became very simple. In [31], authors use Mesh-Tensorflow to train a 5B parameter transformer model that surpasses state-of-the-art results on machine translation tasks.
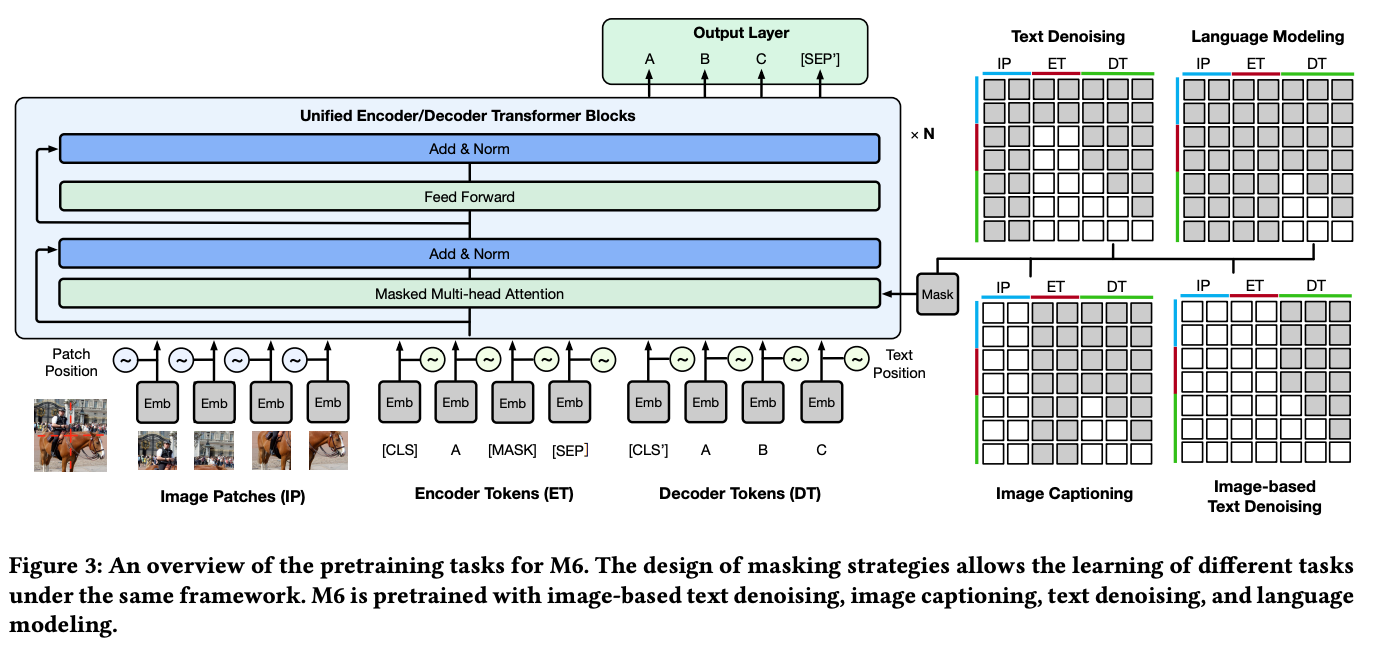
M6 [10] proposes a new (Chinese-only) dataset, which contains 1.9TB worth of images and 292GB of text, for pretraining multi-modal language models. From this dataset, several language models are pretrained using a novel, cross-modal pretraining strategy; see above for a depiction. One of the models that is trained in [10] is a 100B parameter MoE model that replaces all feed-forward sub-layers in the transformer depicted above with MoE layers comprised of 1024 experts.
Scaling Vision with Sparse Mixture of Experts [11]. Although MoE models are clearly beneficial for language modeling, it is unclear whether similar benefits will hold for computer vision. In [11], authors explored a Vision MoE (V-MoE) model that combines the vision transformer architecture with sparse MoE layers; see above. Put simply, we just replace a subset of the feed-forward sub-layers in the vision transformer—such as every other layer or the last n layers—with MoE layers. Such an approach yields a desirable tradeoff between performance and compute. Going further, authors in [11] propose a new routing algorithm that can adaptively leverage more compute for certain inputs at inference time.
“V-MoE matches the performance of state-of-the-art networks, while requiring as little as half of the compute at inference time.” - from [11]
DeepSpeed-MoE [12] observes that performing efficient inference with MoE models is difficult. Scaling up dense LLMs can eventually run into hardware limitations, but MoE models can be scaled (almost) arbitrarily. For this reason, MoE models are a promising architectural advancement, but their adoption is often limited by their larger size and unique architecture. Aiming to make conditional computation easier to use in practice, authors in [12] create the DeepSpeed-MoE framework for end-to-end training and inference of MoE models. This framework defines several MoE architectures, proposes model compression techniques that reduce MoE size up to 3.7X, and implements an optimized inference engine that can improve latency by 7.3X.
Beyond English-Centric Multilingual Machine Translation [23]. This work creates a Many-to-Many machine translation model that can translate directly between any pair of 100 languages. While prior models are highly English-centric, authors in [23] aim to create a model that better reflects translation needs worldwide. First, an open-source training dataset is created that contains supervised language translation examples across thousands of language pairs. To learn from this data, we need a model with sufficient capacity. Authors in [23] explore high-capacity models that combine dense scaling—or just increasing the size of the model—with the use of sparse, language-specific groups of parameters.
GLaM [25] extends the work of Switch Transformers (i.e., applied to encoder-decoder transformer architectures [26]) to decoder-only language models. The goal of this work is to train a GPT-3 quality model more efficiently—using an order of magnitude less compute. GLaM, short for Generalist Language Model, provides a suite of LLMs that use MoE layers to scale up model capacity while maintaining reasonable training costs. The largest model in this suite has 1.2 trillion parameters in total (i.e., 7X larger than GPT-3), performs better than GPT-3 across nearly 30 NLP tasks, is trained using only 1/3 of the energy used for GPT-3, and requires half of the computation of GPT-3 at inference time; see below.
GLaM models use top-two routing (i.e., two active experts in each layer). Authors in [25] also explore larger capacity factors, finding that this metric is useful for controlling the amount of compute used during training or inference.
Final Thoughts
“In deep learning, models typically reuse the same parameters for all inputs. Mixture of Experts (MoE) models defy this and instead select different parameters for each incoming example. The result is a sparsely-activated model—with an outrageous number of parameters—but a constant computational cost.” - from [5]
After studying over two decades of research on MoEs, we should have a decent grasp of the idea, what makes it effective, and how we can apply it to train better language models. Research on this topic has gone through several phases, but the key takeaways from all of this work can be summarized as shown below.
Core idea. The fundamental idea behind an MoE is to decouple a model’s parameter count from the amount of compute that it uses. To do this, we can simply replace layers within the model with several experts that are sparsely activated. Then, a gating mechanism can determine which expert should be used for a given input. In this way, we increase the capacity of the model while only using a portion of the model’s total parameters in the forward pass.
Components of an MoE. There are two primary components of an MoE: i) the experts and ii) a routing mechanism. Each layer has several, similarly-structured experts that can be used to process the input data. Given a set of tokens as input, we use the routing mechanism to (sparsely) select the experts to which each token should be sent. Then, we compute the corresponding experts’ output for each token and combine their results to yield the output of the MoE layer. Many MoE models use some variant of the softmax gating mechanism as a router.
Applying MoEs to transformers. In the language modeling domain, we usually create MoE models based upon the transformer architecture. To do this, we consider every feed-forward sub-layer within the transformer—or some smaller subset of these layers; e.g., every other layer—and replace them with an MoE layer. Each expert in the MoE is a feed-forward neural network with an independent set of parameters that matches the architecture of the initial feed-forward sub-layer. In most cases, top one or top two routing is used for transformer MoE models.
The good and the bad. As we have seen throughout this post, MoE models have many benefits compared to dense models, but they also have many downsides! Given a sufficiently large pretraining dataset, MoE models tend to learn faster than a compute-matched dense model. We can also increase the capacity of an MoE model significantly, allowing the performance of a much larger model to be achieved with a lesser computational burden. This property of MoEs is highly beneficial in settings with tons of training data, hence the popularity of MoEs in the language modeling domain. However, MoE models also:
Consume more memory (i.e., we must store all experts in memory).
Struggle with training stability (though work in [24] helps to solve this).
Tend to overfit during finetuning if there is not enough training data.
All things considered, the choice of whether to use an MoE or not is highly application dependent. If we have nearly unlimited amounts of training data, as is true of most modern language models, then MoEs are highly beneficial and allow us to scale up our model’s capacity significantly, even beyond hardware-imposed limits. In smaller scale applications, however, MoEs are less straightforward to apply compared to dense models and could even perform worse!
New to the newsletter?
Hi! I’m Cameron R. Wolfe, and this is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews of relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on Medium, X, and LinkedIn!
Bibliography
[1] Shazeer, Noam, et al. "Outrageously large neural networks: The sparsely-gated mixture-of-experts layer." arXiv preprint arXiv:1701.06538 (2017).
[2] Eigen, David, Marc'Aurelio Ranzato, and Ilya Sutskever. "Learning factored representations in a deep mixture of experts." arXiv preprint arXiv:1312.4314 (2013).
[3] Bengio, Emmanuel, et al. "Conditional computation in neural networks for faster models." arXiv preprint arXiv:1511.06297 (2015).
[4] Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780.
[5] Fedus, William, Barret Zoph, and Noam Shazeer. "Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity." Journal of Machine Learning Research 23.120 (2022): 1-39.
[6] Kaplan, Jared, et al. "Scaling laws for neural language models." arXiv preprint arXiv:2001.08361 (2020).
[7] Hoffmann, Jordan, et al. "Training compute-optimal large language models." arXiv preprint arXiv:2203.15556 (2022).
[8] Raffel, Colin, et al. "Exploring the limits of transfer learning with a unified text-to-text transformer." The Journal of Machine Learning Research 21.1 (2020): 5485-5551.
[9] Lepikhin, Dmitry, et al. "Gshard: Scaling giant models with conditional computation and automatic sharding." arXiv preprint arXiv:2006.16668 (2020).
[10] Lin, Junyang, et al. "M6: A chinese multimodal pretrainer." arXiv preprint arXiv:2103.00823 (2021).
[11] Riquelme, Carlos, et al. "Scaling vision with sparse mixture of experts." Advances in Neural Information Processing Systems 34 (2021): 8583-8595.
[12] Rajbhandari, Samyam, et al. "Deepspeed-moe: Advancing mixture-of-experts inference and training to power next-generation ai scale." International conference on machine learning. PMLR, 2022.
[13] Jiang, Albert Q., et al. "Mixtral of experts." arXiv preprint arXiv:2401.04088 (2024).
[14] Jiang, Albert Q., et al. "Mistral 7B." arXiv preprint arXiv:2310.06825 (2023).
[15] Jacobs, Robert A., et al. "Adaptive mixtures of local experts." Neural computation 3.1 (1991): 79-87.
[16] Bengio, Yoshua, Nicholas Léonard, and Aaron Courville. "Estimating or propagating gradients through stochastic neurons for conditional computation." arXiv preprint arXiv:1308.3432 (2013).
[17] Davis, Andrew, and Itamar Arel. "Low-rank approximations for conditional feedforward computation in deep neural networks." arXiv preprint arXiv:1312.4461 (2013).
[18] Eigen, David, Marc'Aurelio Ranzato, and Ilya Sutskever. "Learning factored representations in a deep mixture of experts." arXiv preprint arXiv:1312.4314 (2013).
[19] Cho, Kyunghyun, and Yoshua Bengio. "Exponentially increasing the capacity-to-computation ratio for conditional computation in deep learning." arXiv preprint arXiv:1406.7362 (2014).
[20] Bengio, Emmanuel, et al. "Conditional computation in neural networks for faster models." arXiv preprint arXiv:1511.06297 (2015).
[21] Almahairi, Amjad, et al. "Dynamic capacity networks." International Conference on Machine Learning. PMLR, 2016.
[22] Denoyer, Ludovic, and Patrick Gallinari. "Deep sequential neural network." arXiv preprint arXiv:1410.0510 (2014).
[23] Fan, Angela, et al. "Beyond english-centric multilingual machine translation." Journal of Machine Learning Research 22.107 (2021): 1-48.
[24] Zoph, Barret, et al. "St-moe: Designing stable and transferable sparse expert models." arXiv preprint arXiv:2202.08906 (2022).
[25] Du, Nan, et al. "Glam: Efficient scaling of language models with mixture-of-experts." International Conference on Machine Learning. PMLR, 2022.
[26] Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
[27] Shazeer, Noam. "Glu variants improve transformer." arXiv preprint arXiv:2002.05202 (2020).
[28] Zhang, Biao, and Rico Sennrich. "Root mean square layer normalization." Advances in Neural Information Processing Systems 32 (2019).
[29] Clark, Aidan, et al. "Unified scaling laws for routed language models." International conference on machine learning. PMLR, 2022.
[30] Jordan, Michael I., and Robert A. Jacobs. "Hierarchical mixtures of experts and the EM algorithm." Neural computation 6.2 (1994): 181-214.
[31] Shazeer, Noam, et al. "Mesh-tensorflow: Deep learning for supercomputers." Advances in neural information processing systems 31 (2018).
We can implement MoEs with different expert structures; e.g., more complex architectures or hierarchical MoEs, where each expert is an MoE itself. In practical applications with transformers, experts are usually just feed-forward neural networks.
The total number of parameters is slightly less than 8 x 7B = 56B because only feed-forward sub-layers are converted to MoEs, while the rest of the parameters in the network are shared.
The inference cost of this model will actually be closer to that of a 12B parameter model (i.e., slightly less than that of a 14B parameter model) if we account for shared (non-MoE) layers within the transformer.
This statement is not true for all machine learning models. However, it tends to be true in deep learning and is especially true for language models. For more details, one can see relevant research on neural scaling laws.
To avoid overfitting due to these extra parameters, authors in [19] propose a tree-structured parameterization, in which gating units (i.e., prefixes for patterns within the hidden activations) are stored within each node of the tree.
Extra model capacity is typically most useful when we have a large training dataset, as the added capacity enables the model to “absorb” the knowledge in this vast dataset.
In fact, each expert is guaranteed to receive a non-zero score when using this approach!
Long short term memory (LSTM) networks [4]—the most popular language modeling architecture prior to the popularization of GPT-style LLMs—are a type of recurrent neural network (RNN) that have been modified to better handle long input sequences.
Interestingly, authors in [1] note that only 37-46% of total floating point operations by the LSTM are consumed by experts from the MoE.
Early works in this space study LLM performance as a function of model size. However, later work (e.g., Chinchilla [7]) discovers that performance improves as a function of both model and pretraining dataset size.
The intuition here is that we need to compare at least two experts in each forward pass to be able to effectively learn which experts should be selected.
This sounds complicated, but it just means that the model’s performance improves more quickly with respect to the number of examples observed during training. For example, a model that achieves 95% accuracy after observing 10 training examples is more statistically efficient than a model that achieves 90% accuracy after observing the same number of training examples.
Transfer learning simply refers to the process of finetuning a pretrained model on some data to solve a downstream task.
Both of the tasks that are considered are sub-tasks of the SuperGLUE benchmark.
Concurrent work in [29] performs a similar analysis, where authors propose using higher layer frequency (i.e., converting more feed-forward sub-layers in the transformer to MoE layers) and using top-one routing, similar to the Switch Transformer [5].
However, the size of the training set used to determine the data mixture is thresholded by a maximum size to avoid a few tasks dominating the finetuning process.



































Thanks for this fantastically detailed write-up!
Since I am from a computer vision background I have seen MoEs used for a different modality than text. I have seen them being used "conditionally fuse" information based on the "quality and content" of various inputs.
Imagine a CNN that does semantic segmentation of a scene with multi-modal inputs such as RGB images, infrared image, etc. The model then learns to "weigh" the output of each modality branch. The weighting is conditioned on the inputs. So if the RGB image is washed out due to high exposure because your RGB camera is facing the sun, the model can give the RGB branch a lower weight and prefer information from other branches to produce the segmentation mask output.
Cameron, thiscwas a really excellent overview- shows your impressive command of the materials. Would love to see a book by you on the topic.