Mixture-of-Experts (MoE) LLMs
Understanding models like DeepSeek, Grok, and Mixtral from the ground up...
In an area of study that is rapidly changing, the decoder-only transformer architecture has remained one of the few enduring staples in large language model (LLM) research. This architecture has been used since the proposal of the original GPT model and has remained largely unchanged, aside from minor tweaks to improve efficiency. One of the most meaningful modifications to be explored for this architecture, however, is the Mixture-of-Experts (MoE) layer.
“Using an MoE architecture makes it possible to attain better tradeoffs between model quality and inference efficiency than dense models typically achieve.” - from [11]
MoE-based LLMs introduce sparsity to the model’s architecture, allowing us to significantly increase its size—in terms of the number of total parameters—without a corresponding increase in compute costs. This modification, which has been successfully adopted by recent models like Grok [9] and DeepSeek-v3 [15], makes the exploration of extremely large models more tractable and compute efficient. In this overview, we will learn about the fundamentals of MoEs and explore how this idea has been recently applied to create more powerful LLMs.
Fundamentals of MoEs for LLMs
The MoE-based LLMs that we will study in this overview are based upon the decoder-only transformer architecture. We will not cover the details of this architecture here, but please see this article if you are unfamiliar. The decoder-only transformer is comprised of repeated blocks containing normalization (e.g., layer normalization or RMS layer normalization), masked multi-headed self-attention or a feed-forward transformation, and a residual connection; see below.
In this section, we will cover the fundamentals of MoEs. This explanation is based upon seminal papers that i) proposed the standard MoE layer and ii) extended this idea to be used in transformer architectures. The papers are:
For a more detailed break down of these papers and the origins of the MoE architecture, please see the more detailed overview of these ideas below.
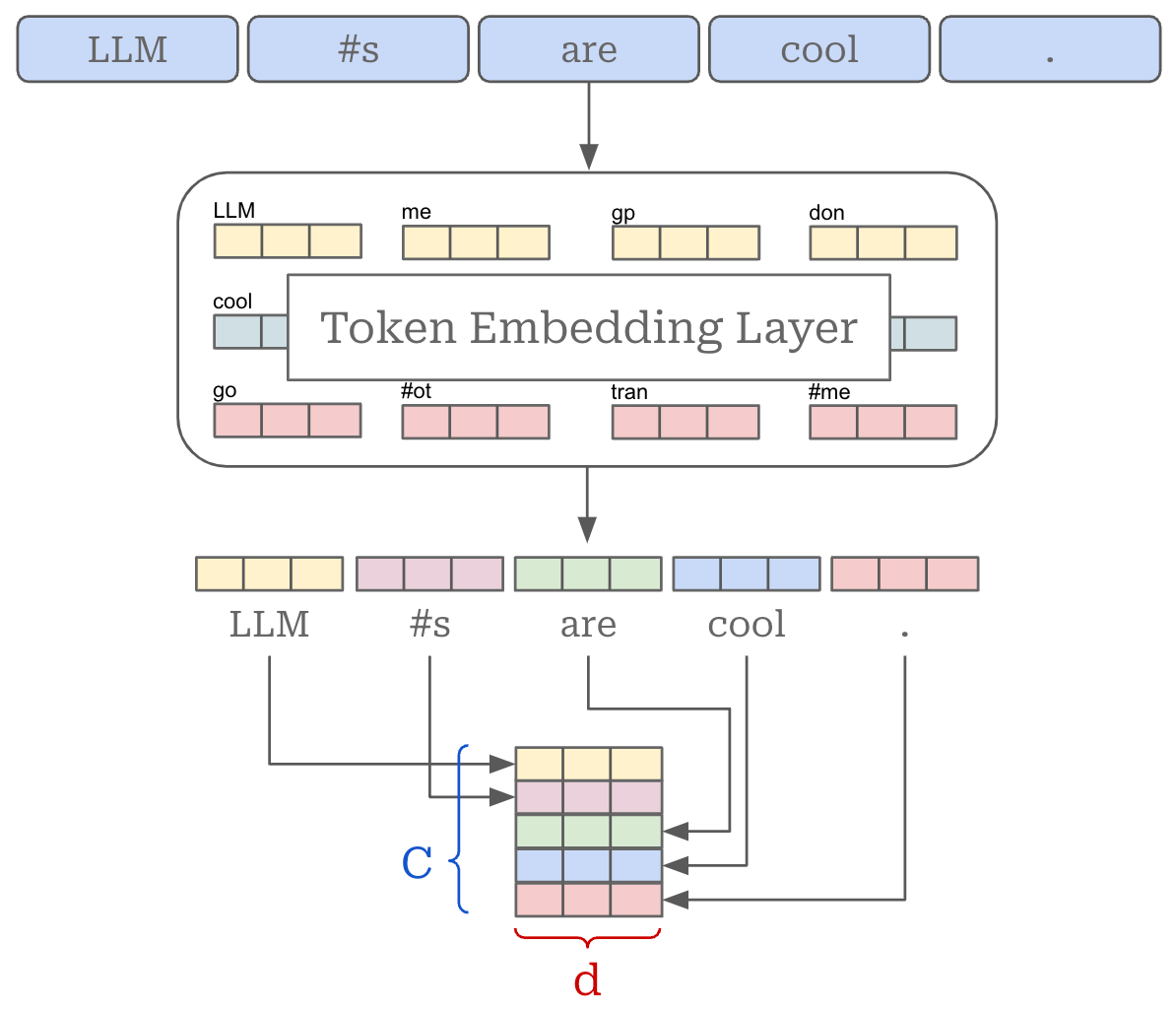
Quick preliminaries. To understand MoEs and routing algorithms, we must first understand the structure of input for the decoder-transformer (and each of its layers). Of course, LLMs take text as input, but this text undergoes extensive processing before the LLM actually sees it. First, the text is tokenized (shown below)—or converted into a list of discrete tokens. These tokens are just words and sub-words. The LLM has a fixed set of tokens that it understands and is trained on, referred to as the model’s “vocabulary”. Vocabulary sizes change between models, but sizes of 64K to 256K total tokens are relatively common.
After the text has been converted to tokens, we can vectorize each token in the input. In addition to having a vocabulary, an LLM has a token embedding layer, which stores a (learned1) vector embedding for every token in its vocabulary. We can lookup the vector for each token in this layer, forming an input matrix. If each token embedding is d-dimensional and there are C total tokens in our input, then the total size of this input matrix is C by d; see below.
Each layer of the transformer—and each sub-layer within every transformer block—maintains the size of this input. As a result, the input (and output) for any feed-forward or attention module in the transformer is a matrix of this same size!
What are “experts”?
In the decoder-only transformer architecture, the main modification made by an MoE is within the feed-forward component of the transformer block. In the standard architecture, we have a single feed-forward neural network—usually made up of two feed-forward layers with a non-linear activation in between—through which every token is passed individually; see below.
An MoE slightly modifies this block structure. Instead of having a single feed-forward network within the feed-forward component of the block, we create several feed-forward networks, each with their own independent weights. We refer to each of these networks as an “expert”. For example, an MoE-based LLM may have eight independent experts in each of its feed-forward sub-layers.
The experts within a transformer layer can be defined as shown above. We have N experts in a layer, and we can refer to the i-th expert using the notation E_i.
Creating an MoE-based transformer. To create an MoE-based decoder-only transformer architecture, we simply convert the transformer’s feed-forward layers to MoE—or expert—layers. Each expert within the MoE layer has an architecture that is identical to the original, feed-forward network from that layer—we just have several independent copies of the original feed-forward network; see below.
However, we need not use experts for every feed-forward layer in the transformer. Most MoE-based LLMs use a stride of P, meaning that every P-th layer is converted into an expert layer and other layer are left untouched—these are “interleaved” MoE layers. This approach can be used to achieve a better balance between the resulting model’s performance and efficiency.
Routing Algorithms
One of the primary benefits of MoE-based architectures is their efficiency, but using experts alone does not improve efficiency! In fact, adding more experts to each layer of the model significantly increases the total number parameters—and the amount of necessary compute—for the model. To make the architecture more efficient, we must sparsely select the experts that should be used in each layer!
Selecting experts. Let’s consider a single token—represented by a d-dimensional token vector. Our goal is to select a subset of experts (of size k) to process this token. In the MoE literature, we usually say that the token will be “routed” to these experts. We need an algorithm to compute and optimize this routing operation.
The simplest possible routing algorithm would apply a linear transformation to the token vector, forming a vector of size N (i.e., the number of experts). Then, we can apply a softmax function to form a probability distribution over the set of experts for our token. We can use this distribution to choose experts to which our token should be routed by simply selecting the top-K experts in the distribution.
This routing strategy was used in [1], the paper that proposed the sparse MoE layer structure that we use today; see above. However, such a routing mechanism does not explicitly encourage a balanced selection of experts. For this reason, the model is likely to converge to a state of repeatedly selecting the same few experts for every token instead of fully and uniformly utilizing its expert layers, as explained below. This phenomenon is commonly referred to as “routing collapse”.
“The gating network tends to converge to a state where it always produces large weights for the same few experts. This imbalance is self-reinforcing, as the favored experts are trained more rapidly and thus are selected even more by the gating network.” - from [1]
Active parameters. Because we only select a subset of experts to process each token within an MoE layer, there is a concept of “active” parameters in the MoE literature. Put simply, only a small portion of the MoE model’s total parameters—given by the experts selected at each MoE layer—are active when processing a given token. As a result, the total computation performed by the MoE is proportional to the number of active parameters, rather than the total number of parameters.
Auxiliary Losses and Expert Load Balancing
To encourage a balanced selection of experts during training, we can simply add an additional constraint to the training loss that rewards the model for uniformly leveraging each of its experts. In [1], this is done by defining an “importance” score for each expert. The importance score is based upon the probability predicted for each expert by the routing mechanism.
Given a batch of data, we compute importance by taking a sum of the probabilities assigned to each expert across all tokens in the batch; see above. Then, to determine if these probabilities are balanced, we can take the squared coefficient of variation (CV) of the expert importance scores. Put simply, the CV will be a small value if all experts have similar importance scores and vice versa.
From here, we can simply add the importance loss shown above to our standard language modeling loss to from our new (regularized) training objective. This additional importance loss term helps to ensure that the MoE assigns equal probability to experts throughout the training process.
Load balancing. Although the importance loss described above is useful, just because experts are assigned equal importance does not mean that tokens are routed uniformly. For example, experts would have equal importance with:
A few tokens that assign them very high probability.
A much larger number of tokens that assign lower probability.
As a result, the number of tokens dispatched to each expert can still be highly non-uniform even when using an importance loss, which can lead to excessive memory usage and generally degraded efficiency for the MoE2.
To solve this problem, we can create a single auxiliary loss term (shown above) that captures both expert importance and load balancing, defined as the equal routing of tokens between each of the experts. Such an approach is proposed in [2], where authors create a loss that considers two quantities:
The fraction of router probability allocated to each expert3.
The fraction of tokens dispatched to each expert.
If we store both of these quantities in their own N-dimensional vectors, we can create a single loss term by taking the dot product4 of these two vectors. The resulting loss is minimized when experts receive uniform probability and load balancing, thus capturing both of our goals within a single auxiliary loss term!
Router z-loss. The auxiliary load balancing loss described above is widely used throughout the MoE literature, but authors in [3] propose an extra auxiliary loss term, called the router z-loss, that can further improve training stability. The router z-loss constrains the size of the logits—not the probabilities, so this is before softmax is applied—predicted by the routing mechanism. Ideally, we do not want these logits to be too big. However, these logits can become very large—leading to round-off errors that can destabilize the training process even when using full (float32) precision—when passed through the router’s (exponential) softmax function.
“The router computes the probability distribution over the experts in float32 precision. However, at the largest scales, we find this is insufficient to yield reliable training.” - from [3]
To encourage the router to predict smaller logits, we can use the loss term shown above. Given that this loss focuses solely upon regularizing the router’s logits and performs no load balancing, we typically use the router z-loss in tandem with the auxiliary load balancing loss proposed in [2]. Both of these losses are added on top of the LLM’s standard language modeling loss; see below.
Expert Capacity
The computation performed in an MoE layer is dynamic due to the routing decisions made during both training and inference. However, when we look at most practical implementations of sparse models, we will see that they usually have static batch sizes—this is a useful trick for improving hardware utilization.
Expert capacity. To formalize the fixed batch size that we set for each expert, we can define the expert capacity. The expert capacity is defined as shown below.
The expert capacity defines the maximum number of tokens in a batch that can be sent to each expert. If the number of tokens routed to an expert exceeds the expert capacity, then we just “drop” these extra tokens. More specifically, we perform no computation for these tokens and let their representation flow directly to the next layer via the transformer’s residual connection.
“To improve hardware utilization, most implementations of sparse models have static batch sizes for each expert. The expert capacity refers to the number of tokens that can be routed to each expert. If this capacity is exceeded then the overflowed tokens… are passed to the next layer through a residual connection.” - from [3]
Expert capacity is controlled via the capacity factor setting. A capacity factor of one means that tokens are routed in a perfectly balanced manner across experts. Alternatively, setting the capacity factor above one provides extra buffer to accommodate for an imbalance in tokens between experts. However, this comes at a cost (e.g., higher memory usage and lower efficiency).
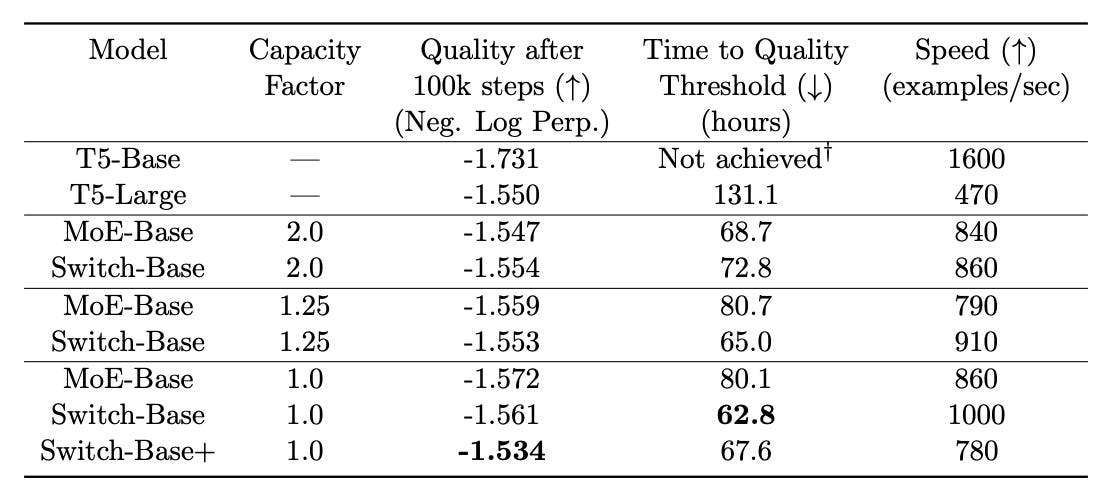
How do we set the capacity factor? Interestingly, MoE models tend to perform well with relatively low capacity factors [2, 3]; see above. However, we need to ensure that the number of dropped tokens is not too large (i.e., this can be done empirically) to avoid any impact to the training run. We can also use different capacity factors for training and inference; e.g., ST-MoE [3] uses a capacity factor of 1.25 during training and a capacity factor of 2.0 during evaluation.
Computing the Output of an MoE Layer
Once we have the router’s output, we compute the final output as follows:
Send the tokens to their selected experts.
Compute the output of the experts for these tokens.
Take a weighted average of expert outputs, where the weights are simply the probabilities assigned to each expert by the router.
In the equation above, we have formalized the process for computing the output of the MoE layer for a single token. The output for this token is just a weighted average of the outputs from each of its K active experts.
Shared experts are an idea that has been more recently introduced in the MoE literature [14, 15]. The idea is simple:
We have two groups of experts—shared experts and routed experts.
All tokens are always passed through the shared experts.
Tokens are passed through the routed experts according to a normal MoE routing mechanism.
This idea of shared experts is depicted below, where we see that routing is only applied to a subset of the experts within an MoE layer. Usually, the number of shared experts must be lower than the number of routed experts—increasing the number of shared experts degrades the sparsity benefits of the MoE.
The motivation behind using shared experts is minimizing the amount of redundant information between experts. By having a set of shared experts, we can allow the network to store shared information within these experts, rather than having to replicate the same information across several different experts. To compute the output of an MoE layer with shared experts, we simply add the shared experts’ output to the normal, routed output; see below.
Putting it all Together: Decoder-only LLMs with MoE Layers
A full depiction of an MoE layer is provided above. In an MoE, we modify the block structure of the standard decoder-only transformer by replacing the feed-forward network with an expert layer. Put simply, this expert layer contains several independent copies of the original feed-forward network. Notably, all of these components within the MoE layer—the normal layer(s), the experts, and the routing mechanism—are trained jointly via gradient descent.
For each token, we can choose which experts to be used via a routing mechanism, which is usually implemented via a simple linear transformation of the token vector. Putting this together, the modified block structure for an MoE contains:
A self-attention layer.
A residual connection and a normalization operation.
A routing mechanism that determines the routing of tokens to experts.
An expert layer with multiple independent feed-forward networks.
A final add and normalize operation that is applied to the final output of the expert layer for each token.
Aside from the modified block structure, the transformer architecture remains the same. We also only convert every P-th block of the transformer to use an MoE layer—other blocks remain unchanged. Some MoEs use experts at every layer, but it is common to set P to two, four, or even six in practice. This trick can be useful for controlling the total number of parameters consumed by the MoE LLM.
The Pros and Cons of Using MoEs
Now that we understand the basics of MoEs, we might wonder: Why would we want to use an MoE instead of a dense model? The biggest selling point of MoEs is their efficiency, but these models also have notable drawbacks. Let’s quickly go over some of the most important pros and cons of MoEs to be aware of.
Benefits of MoEs. LLMs benefit from scale—larger models and larger datasets lead to better performance. However, scaling up LLMs comes at a cost! One of the key benefits of MoEs is their ability to circumvent issues with scaling up—they allow us to increase the size of our model at a fixed computational cost per token. This way, we can train larger models than would be possible if we restricted ourselves to only dense models. In the language modeling domain, the extra parameters and representational capacity of these sparse models make a big difference.
“As LLMs become increasingly prevalent, enhancing their performance without proportionally increasing computational resources is a critical challenge.” - from [12]
The computational benefit of MoEs is (arguably) most impactful during inference. MoE models are large in terms of their number of total parameters, so we need a sufficient number of GPUs available to store these parameters. However, we only use a fixed portion of these parameters when processing each token, which drastically improves compute efficiency. Inference is faster at low batch sizes, and throughput is higher at large batch sizes [5]. Interestingly, MoEs are also more efficient to train. For example, the Switch Transformer reported a 7× pretraining speedup from the use of an MoE architecture [2]; see below.
Drawbacks of using MoEs. Despite these benefits, MoEs are also:
Prone to instabilities during training.
Difficult to finetune (i.e., due to issues with overfitting).
Sensitive to low / mixed precision training techniques.
Sensitive to hyperparameter settings (e.g., weight initialization).
Put simply, there are more bells and whistles required to get the most out of an MoE. For this reason, MoEs may not be the best choice in every scenario; e.g., a dense model may be an easier choice if we are looking to finetune an LLM on some task. However, if we can use them properly, MoEs have a variety of benefits.
Mixture-of-Experts Language Models
Now that we understand the most important and fundamental concepts of MoEs, lets take a deeper look at how these concepts have been applied in the language modeling domain. Due to the fact that LLMs benefit from increased scale, MoEs have been widely adopted and seen great success within LLM research.
Mixtral of Experts [5]
Mixtral 8×7B (a.k.a. Mixtral of Experts) is an MoE-based extension of the open-source Mistral-7B model [6] that is fluent in English, French, Italian, German, and Spanish. Both of these models have open weights under an Apache 2.0 license, as well as corresponding technical reports that provide details about the models.
Mixtral converts every layer of Mistral to an expert layer with eight experts. Two of these experts are active for each token, yielding a model with 47 billion total parameters and 13 billion active parameters. The model also has a context length of 32K, which is 4× larger than its non-MoE counterpart. As shown in the figure above, Mixtral outperforms Mistral across the board and especially excels in code generation, math, and multilingual benchmarks, even exceeding the performance of the larger LLaMA-2-70B model in some cases.
Mistral-7B architecture. The base LLM architecture for Mixtral 8×7B is a decoder-only transformer that exactly matches the architecture settings of Mistral-7B [6]. Compared to the standard decoder-only LLM architecture, there are a few changes made by Mistral-7B:
Grouped-Query Attention (GQA) [7]: shares key and value projections between groups of self-attention heads to improve efficiency; see above.
Sliding Window Attention (SWA) [8]: computes (masked) self-attention over a fixed window of size
Wfor each token to allow the LLM to handle sequences of arbitrary length with a reduced inference cost5; see below.
Because we use SWA, the model can use tricks like rolling buffer / circular caches to make the KV cache more memory efficient or chunked prefill to increase inference speed. Mixtral 8×7B adopts the same architecture conventions.
More details. As mentioned previously, Mixtral converts every layer of the LLM to an expert layer. Within each expert layer, a simple routing mechanism is adopted that takes a softmax over the Top-K logits of a linear layer for every token—this matches the routing mechanism discussed at the start of this overview; see below.
Authors mention in [5] that Mixtral is also pretrained over a multilingual corpus, allowing the model to understand multiple languages. As shown below, Mixtral universally outperforms LLaMA models on multi-lingual benchmarks.
Routing analysis. To conclude the paper, authors in [5] perform some detailed analysis of how experts are selected for tokens across several domains to see if any interpretable patterns can be deduced. When we plot the distribution of tokens assigned to different experts for various topic areas within The Pile, there are no obvious patterns in token assignment that arise; see below.
However, the MoE does exhibit some structured behavior. For example, the words “self” in Python code and “Question” in English—even though they are comprised of multiple tokens—often get routed through the same expert. Similarly, indentation tokens in code are usually sent to the same expert, and consecutive sequences—just sequences of tokens that are close to each other—generally are sent to the same expert; see below. These results indicate that i) experts are not specialized by topic but ii) the MoE’s routing mechanism does obey some structured behavior with respect to the syntax or contents of the model’s input.
Scaling up. After Mixtral, a larger version of the model was released, called Mixtral-8×22B. This model has 141 billion total parameters and 39 billion active parameters, making it ~3× larger than the original Mixtral model. Mixtral-8×22B is especially capable on coding and mathematics tasks, has an expanded context length of 64K, and is natively capable of function calling. The key benefits of Mixtral-8×22B compared to other open models are summarized below.

Grok (from xAI) [9]
Although there is no detailed technical report on the model, one of the most notable recent examples of MoE-based LLMs is xAI’s Grok. The initial Grok-1 model was released in early 2024. Researchers revealed that the model is a 314 billion parameter MoE with 25% of weights active for each token (i.e., ~70-80 billion active parameters). The architecture and base model weights of Grok-1 were open-sourced under and Apache 2.0 license. However, this is a pretrained base model, and no details were provided on the model’s post training process.
Grok-1.5 [10]. Shortly after the initial release of Grok-16, a follow-up version of the model was published with better reasoning and long context understanding capabilities. For example, Grok-1.5 performs much better on math and coding-related tasks; see above.
“The model can handle longer and more complex prompts, while still maintaining its instruction-following capability as its context window expands.” - from [10]
Grok-1.5 can process sequences up to 128K tokens with perfect retrieval on the needle in a haystack test; see below. Authors also note that the model maintains solid instruction-following capabilities when given a lot of context, which is a much better sign of long context capabilities compared to pure retrieval7.
Given that Grok-1.5 and Grok-1 were released in such close succession, we can infer that the advancements made by Grok-1.5 are driven by post training—it is extremely unlikely that a different pretrained base model was created during this time.
Grok-2. More recently, Grok-2 was released, which has improved reasoning, coding, and chat—as measured by Chatbot Arena—capabilities. Grok-2 also has a variety of other small improvements (e.g., tool usage, retrieval, factuality, etc.) and a distilled version of Grok-2, called Grok-2-mini, was released with the main model. However, no public details were shared about the architecture of Grok-2—the model was likely trained from scratch and may or may not be MoE-based.
DBRX (from Mosaic) [11]
DBRX is the latest model in the series of Open LLMs released by Mosaic. Two versions of the model were released—a base model (DBRX base) and a finetuned model (DBRX Instruct)—under an open license (i.e., the Databricks open model license). DBRX is an MoE-based LLM with the following specifications:
132 billion total parameters with 36 billion active parameters.
16 experts in each MoE layer with 4 experts active for each token.
Pretrained on 12 trillion tokens of optimized text.
4× improvement in pretraining efficiency.
Most notably, DBRX is a “fine-grained” MoE model. In other words, the model uses a larger number of experts in each MoE layer, but each individual expert is smaller. For reference, both Mixtral and Grok-1 contain eight experts—two of which are active for any given token—within each of their MoE layers. By using fine-grained experts, each MoE layer has more expert combinations (65× more in particular) to choose from, which was found to improve quality in [11].
Training data. The pretraining dataset for DBRX is very large8, but authors in [11] also invest significantly into improving the quality of the data. As a result, the statistical training efficiency of DBRX is higher than normal—training is faster because we achieve higher accuracy with fewer tokens. More specifically, authors in [11] estimate that the new data is 2× more efficient token-for-token, meaning that we can train over half as many tokens and achieve the same level of performance. This claim was verified by testing the impact of the new model’s pretraining data in isolation (i.e, using a fixed model with different pretraining data).
“In isolation, better pretraining data made a substantial impact on model quality. We trained a 7B model on 1T tokens using the DBRX pretraining data. It reached 39.0% on the Databricks Gauntlet compared to 30.9% for MPT-7B.” - from [11]
Additionally, curriculum learning is used to train DBRX—the mixture of pretraining data is dynamically changed throughout the pretraining process. The details of this curriculum learning strategy were later outlined in this paper. The curriculum learning strategy used by DBRX just upsamples smaller, domain-specific datasets towards the end of training because this data is higher quality relative to data obtained via web-crawling. This simple curriculum learning strategy is found to provide a significant boost in performance on difficult benchmarks; see below.

Tokenizer and context window. DBRX has a context length of 32K and uses the GPT-4 tokenizer (available via tiktoken). According to the authors, the GPT-4 tokenizer was selected mostly due to performance. This tokenizer has a large vocabulary and is very token efficient, which naturally improves decoding and training speed by representing the same amount of text with fewer tokens.
Efficiency wins. The proposal of DBRX comes with large improvements in terms of pretraining efficiency. Beyond what we have learned about so far, there are several additional sources of efficiency gains mentioned in [11]:
The MoE architecture, which is found in smaller-scale experiments to require 1.7× fewer FLOPS during training.
Other modifications to the decoder-only architecture (i.e., RoPE, GLU activation, and GQA).
“Better optimization strategies”.
When considering all data, architecture, and optimization changes, the end-to-end training process for DBRX requires 4× less compute when compared to the pretraining pipeline used for prior models. To determine this number, authors in [11] compare a smaller variants of DBRX to their prior MPT-7B model, finding that the smaller DBRX models achieve similar performance on the Databricks Gauntlet while using 3.7× fewer FLOPS during training.
DBRX also comes with improvements to inference efficiency—up to 2× faster than LLaMA-2-70B at 150 tokens per second per user in load tests. These measurements are made using an optimized serving infrastructure with TensorRT-LLM and 16 bit precision, which is very fast. The MoE architecture of DBRX also aids inference efficiency due to the relatively low number of active parameters. For example, DBRX is 40% of the size of Grok-1 in both total and active parameters.
“Training mixture-of-experts models is hard. We had to overcome a variety of scientific and performance challenges to build a pipeline robust enough to repeatably train DBRX-class models in an efficient manner.” - from [11]
Training MoEs is generally difficult due to instabilities that arise during training, communication bottlenecks, and more. However, DBRX achieves impressive results in terms of stability, efficiency, and performance due to the optimized pretraining strategy outlined in [11]. Notably, there is not single change or advancement that enables these results. The impressive pretraining pipeline used by DBRX is enabled by a large number of small, practical changes.
Empirical evaluation. In comparison to other open LLMs, we see that DBRX-Instruct achieves better performance on composite benchmarks by a large margin when compared to Mixtral; see below. Despite being a general-purpose LLM, DBRX has impressive programming skills, outperforming Grok-1 (more than twice its size!) and even specialized coding models like CodeLLaMA-70B. DBRX also performs well on reasoning and math-based tasks.
Compared to closed models, DBRX surpasses the performance of GPT-3.5 and is competitive with Gemini-1.0 Pro. Gemini-1.0 Pro only outperforms DBRX on GSM8K, while Mixtral-Medium performs better on a select few tasks that are considered; see below. At a high level, DBRX seems to be good at programming, math, general knowledge, commonsense reasoning, and retrieval / RAG.
OpenMoE: An Early Effort on Open Mixture-of-Experts Language Models [12]
Despite the success of MoEs in the language modeling domain, the number of truly open-source MoEs—meaning that code, information, data, weights and more are all shared publicly—is relatively low. To solve this issue, OpenMoE [12] conducts a large-scale effort to train a suite of decoder-only MoE LLMs ranging from 650 million to 34 billion parameters. These models adopt fine-grained experts with varying granularity (i.e., 16 or 32 experts). The findings from this effort are documented in [12] and all models are shared openly. The authors also provide a well-documented code repository that can be used to reproduce their results.
“Using an MoE every layer introduces more computational overhead during routing and induces a worse cost-effectiveness trade-off than interleaved MoE usage.” - from [12]
Design choices. OpenMoE models adopt the settings of ST-MoE [3], including the same routing mechanism and number of active experts (i.e., k = 2). Authors choose to covert only every fourth or sixth transformer block to an MoE layer, finding that larger strides yield a better tradeoff in terms of cost and efficiency.
The pretraining dataset used for OpenMoE contains a heavy distribution of code. In fact, code comprised over 50% of the dataset during the early phases of pretraining, but this ratio was adjusted later in training due to being sub-optimal; see below. For alignment, OpenMoE undergoes SFT after pretraining—using the data from WildChat—to induce better instruction-following capabilities.
Routing dynamics. One of the key contributions of OpenMoE is a detailed analysis of the routing decisions made within the models. First, we see that—similarly to results shown in prior work [5]—experts do not tend to specialize in any particular domain; see below.
However, we do see some level of expert specialization across natural languages and specific tasks, as shown in the figure below.
When we dig into this trend, however, we see that the dynamics of token routing are primarily dictated by the token ID. In other words, the same token will almost always be routed to the same expert, no matter the context in which that token exists. This pattern is referred to as “Context-Independent Specialization” in [12].
“This is a very interesting finding because the tokens with the same Token ID have very diverse contexts in different sentences. For instance, the token ‘an’ can also be part of ‘an apple’ or ‘another’. However, all these tokens have very strong specialization on only a few fixed experts.” - from [12]
Interestingly, experts have observable patterns in the tokens that they prefer; see below. For example, “have”, “has” and “had” are all routed to the same expert, while one expert receives the “=”, “and” and “\n” tokens—very common tokens within coding languages. We see in [12] that such routing patterns are solidified during the early stages of pretraining and rarely change later in training.
Routing issues. Beyond the routing patterns observed in [12], we also see that OpenMoE models exhibit some routing behaviors that could damage their performance. For example, the models tend to drop tokens later in the sequence, which can damage performance on long sequence tasks (e.g., multi-turn chat).
Because routing dynamics are fixed during the early phases of the pretraining process, these behaviors are hard to fix during post training. In fact, OpenMoE models are observed to generally struggle with the domain gap between data during pretraining and SFT9—the token routing dynamics become sporadic due to the difference in data composition. To solve these issues, authors in [12] recommend mixing instruction-following data into the pretraining dataset.
Model evaluation. Overall, OpenMoE models do not set new state-of-the-art performance among MoE LLMs—authors in [12] openly state this fact and admit that the performance of OpenMoE models could be greatly improved through better design. The larger contribution of OpenMoE models is their transparency. The details and artifacts publicly shared in [12] can accelerate open research efforts on MoEs by providing necessary resources to conduct further research on this topic.
DeepSeek-v2 [14] and DeepSeek-V3 [15]
The recently-proposed DeepSeek MoE models, including DeepSeek-v2 [14] and DeepSeek-v3 [15], have made waves within the LLM research community for a variety of reasons:
Their weights are shared publicly.
They come with technical reports that share many details.
Their performance is impressive—on par with many closed models.
Their training costs are pretty reasonable.
As we will see, the DeepSeek models make a variety of unique design choices that maximize both their training efficiency and downstream performance.
DeepSeek-v2 [14]—a 236 billion parameter MoE with 21 billion active parameters—proposes the MoE architecture used by the later DeepSeek-V3 model. The DeepSeek MoE models are a bit different than prior models, as they slightly modify the underlying transformer block to boost performance and efficiency. As shown below, the DeepSeek-v2 model—in addition to performing well—is quite impressive from a training and inference efficiency perspective, making it a strong starting point for the much larger DeepSeek-v3 model.
Multi-head latent attention (MLA). Instead of standard, multi-headed attention, DeepSeek-v2 adopts MLA, which is an efficient attention variant. Similarly to multi-query attention or grouped-query attention, MLA aims to minimize memory consumed by the model’s KV cache. Unlike other efficient attention variants, however, MLA does not have a significant performance tradeoff.
In particular, this gain in memory efficiency is achieved via a low-rank, joint projection that allows us to represent all key and value vectors with a much smaller (latent) vector; see above. We can upsample this vector—just linearly project it to form several, larger vectors—to restore the full key and value vectors, but we only have to store the latent vector in our KV cache, thus drastically reducing memory consumption. Adopting MLA decreases the size of DeepSeek-v2’s KV cache by over 93% compared to a 67 billion parameter dense model.
DeepSeek MoE architecture. Beyond using MLA, DeepSeek models adopt a unique MoE layer structure. Similar to DBRX, these models use fine-grained experts. However, a subset of these experts are shared. The motivation for adopting such a structure is to encourage specialization among a larger number of experts while minimizing redundant information between experts. A full schematic of the block structure used by DeepSeek models is provided below.
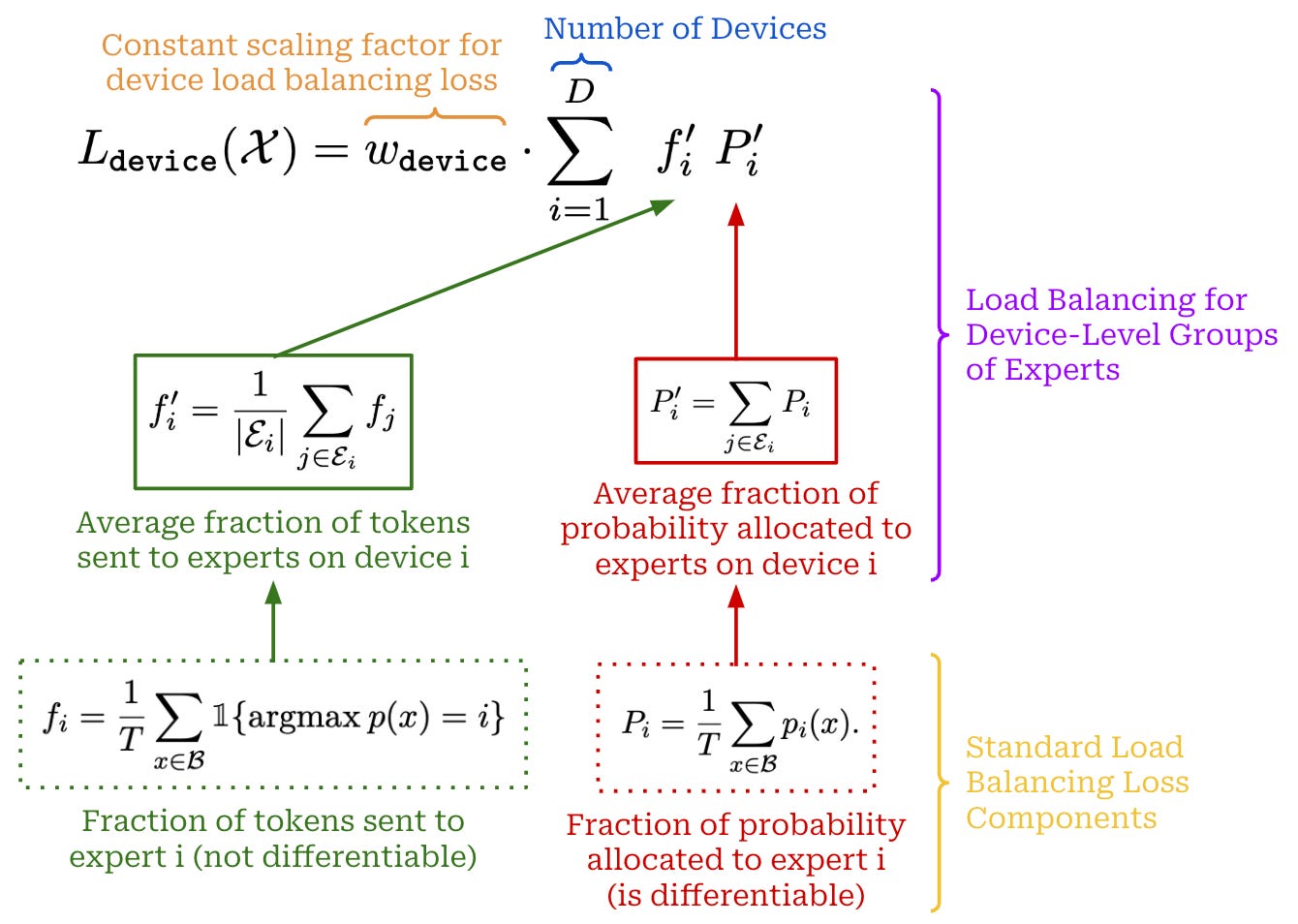
Authors in [14] also adopt an interesting load balancing strategy for handling the fine-grained experts used by DeepSeek-v2. In addition to using the auxiliary load balancing loss proposed in [2], DeepSeek-v2 has two auxiliary loss terms that aim to balance communication between devices during distributed training.
Using fine-grained experts means that we must dispatch each token to a larger number of experts. In a distributed training setting, experts may be on different devices and multiple experts reside on each device. To ensure communication and computation are balanced between devices, we need additional auxiliary losses that i) group experts by the device on which they reside and ii) encourage the MoE to perform balanced routing on a per-device basis. For example, the auxiliary loss shown above encourages balanced computation among devices. There is an extra loss proposed in [14] to encourage balanced communication among devices as well.
DeepSeek-v3 [15] is a much larger version of DeepSeek-v210, having 671 billion total parameters and 37B active parameters. This larger model is pretrained on a massive corpus comprised of 14.8 trillion tokens. After pretraining, a multi-phase post training pipeline is applied:
The model first undergoes a two-stage context extension procedure in which it is finetuned (via SFT) to have a maximum context length of 32K, then further finetuned to have a context length of 128K.
After context extension, the model undergoes further SFT and RLHF to align it to human preferences.
Capabilities from the recently-proposed R1 reasoning model are also distilled into DeepSeek-v2 during post training.
The final DeepSeek-v3 model outperforms closed-source models and achieves similar performance to even the best closed LLMs; see above. DeepSeek-v3 also makes several modifications to the training and load balancing strategy for the MoE, leading the model’s training process to be both efficient and stable.
“Despite its excellent performance, DeepSeek-V3 requires only 2.788M H800 GPU hours for its full training. In addition, its training process is remarkably stable… we did not experience any irrecoverable loss spikes or perform any rollbacks.” - from [15]
The architecture of DeepSeek-v3 is inspired by its predecessor; e.g., MLA, fine-grained experts, and shared experts are all used by DeepSeek-v3. Unlike DeepSeek-v2, however, DeepSeek-v3 uses a Multi-Token Prediction (MTP) training objective. This objective is an extension of the supervised, cross entropy-based next token prediction objective that is used almost universally for training LLMs. Instead of predicting the next token for each token within a sequence, MTP predicts D future tokens. These predictions are made sequentially by a set of additional modules that are added to the model’s architecture; see below.
Once several future tokens have been predicted, we can apply the cross-entropy loss normally. Applying this loss over several future tokens predicted via MTP provides a richer training signal to the model, which improves training efficiency and overall performance. Going further, these additional modules used for MTP can also be used to improve inference efficiency via speculative decoding. However, authors in [15] state that the MTP strategy is used purely to benefit model performance—additional modules are discarded after training.
An auxiliary-loss-free load balancing strategy is also used by DeepSeek-v3 that simply adds a per-expert bias term to the selection of Top-K experts; see above. At each iteration, the bias term for each expert is either increased or decreased by a fixed factor γ based upon whether that expert was underloaded or overloaded, respectively. Importantly, these biases are only used when selecting the top-K experts—they do not impact the computation of expert probability within the router. This approach is found to effectively balance expert utilization within the MoE and eliminate performance deterioration due to the use of load balancing losses. However, authors in [15] do note that they still use an auxiliary load balancing loss (with a very low scaling factor) when training DeepSeek-v3.
Training efficiency. Due to the efficiency and performance benefits of the strategies outlined above, DeepSeek-v3 is incredibly economical. Plus, the model is trained using a novel FP8 mixed precision training framework, marking the first validation of 8-bit training for large-scale LLMs. In total, training the final model was estimated11 to cost ~$5.6M; see above. In short, the DeepSeek-v3 is:
Trained in a very economical fashion (and with several novel advancements like FP8 training and MTP!)
Incredibly impressive for an open model—highly competitive with even the best closed LLMs.
Based on an interesting MoE architecture with several novel modifications.
Reasoning. DeepSeek-v3 also serves as a base model for DeepSeek-R1 [13], a recently-released open reasoning model. Put simply, R1 is an open replication of the o1-style of models that have been recently explored by OpenAI. As explained in its detailed technical report, this model uses pure reinforcement learning to learn how to solve complex (verifiable) reasoning tasks by crafting extremely long chains of thought. As shown in the figure below, the performance of R1 is quite impressive, especially for an open model. However, the capabilities of R1 would not be possible without first having access to an incredibly-capable base model.
Final Thoughts
MoEs have many benefits that are especially suited to language modeling. They enable exploration of larger scales without drastic increases in compute, reduce training costs, and can be efficiently hosted. Although the idea of sparsity has existed for a long time within the machine learning literature, MoEs are an especially impactful instantiation of sparsity. They leverage sparsity in a manner that is compatible with modern hardware and can be practically implemented on a GPU. Interestingly, early MoE variants struggled with adoption due to their complexity, instability, and difficulty of use. However, the advancements we have seen in this overview have turned the MoE into something practical and impactful—a simple and promising extension of the decoder-only transformer architecture.
New to the newsletter?
Hi! I’m Cameron R. Wolfe, Deep Learning Ph.D. and Machine Learning Scientist at Netflix. This is the Deep (Learning) Focus newsletter, where I help readers better understand important topics in AI research. If you like the newsletter, please subscribe, share it, or follow me on X and LinkedIn!
Bibliography
[1] Shazeer, Noam, et al. "Outrageously large neural networks: The sparsely-gated mixture-of-experts layer." arXiv preprint arXiv:1701.06538 (2017).
[2] Fedus, William, Barret Zoph, and Noam Shazeer. "Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity." Journal of Machine Learning Research 23.120 (2022): 1-39.
[3] Zoph, Barret, et al. "St-moe: Designing stable and transferable sparse expert models." arXiv preprint arXiv:2202.08906 (2022).
[5] Jiang, Albert Q., et al. "Mixtral of experts." arXiv preprint arXiv:2401.04088 (2024).
[6] Jiang, Albert Q., et al. "Mistral 7B." arXiv preprint arXiv:2310.06825 (2023).
[7] Ainslie, Joshua, et al. "GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints." arXiv preprint arXiv:2305.13245 (2023).
[8] Beltagy, Iz, Matthew E. Peters, and Arman Cohan. "Longformer: The long-document transformer." arXiv preprint arXiv:2004.05150 (2020).
[9] xAI. “Open Release of Grok-1” https://x.ai/blog/grok-os (2024).
[10] xAI. “Announcing Grok-1.5” https://x.ai/blog/grok-1.5 (2024).
[11] Mosaic Research (Databricks). “Introducing DBRX: A New State-of-the-Art Open LLM” https://www.databricks.com/blog/introducing-dbrx-new-state-art-open-llm (2024).
[12] Xue, Fuzhao, et al. "Openmoe: An early effort on open mixture-of-experts language models." arXiv preprint arXiv:2402.01739 (2024).
[13] Guo, Daya, et al. "DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning." arXiv preprint arXiv:2501.12948 (2025).
[14] Liu, Aixin, et al. "Deepseek-v2: A strong, economical, and efficient mixture-of-experts language model." arXiv preprint arXiv:2405.04434 (2024).
[15] Liu, Aixin, et al. "Deepseek-v3 technical report." arXiv preprint arXiv:2412.19437 (2024).
In other words, the contents of this embedding layer are updated (via gradient descent) throughout the training process, similarly to any other model parameter.
To improve both hardware (i.e., GPU utilization, throughput, etc.) and statistical (i.e., how quickly the model learns from data) efficiency, we want to have a relatively uniform number of tokens dispatched to all experts in each batch of data.
This quantity is predicted by our routing algorithm and is, therefore, differentiable. So, the loss function as a whole is differentiable even though the fraction of tokens sent to each expert is not itself a differentiable quantity.
We also have to multiple this loss term by N to ensure that the loss remains constant as the number of experts is increased.
It may seem like SWA limits each token to only “look at” a few tokens within a sequence. However, if we stack k consecutive layers of SWA on top of each other, the effective context window for each token increases. The representation of the current token is actually influenced by the k⋅W tokens that come before it.
Both of these models were released in March of 2024 within ~10 days of each other!
The needle in a haystack test tests an LLM’s ability to retrieve information in its context. However, the model may still have bad long context abilities even if it scores perfectly on the needle in a haystack test; e.g., instruction-following or reasoning capabilities could get way worse when given a long context.
We encounter much different styles of data during SFT compared to pretraining; e.g., multi-turn chat data, instruction templates, and more.
Between these models, DeepSeek also released an intermediate model, called DeepSeek-v2.5; see here for details.
These estimates are made by assuming a $2 rental price per H800 GPU hour. Additionally, they reflect the pure compute cost of training the final model only, excluding any supplemental costs or experiments. The actual total cost of training DeepSeek-v3 is undoubtedly much larger than this reported number.















































Great deep dive and very helpful. Thanks for writing this!
Amazing article, a true gem. I would be interested to learn more about how DeepSeek used reinforcement learning to such great effect.