Scaling Laws for LLMs: From GPT-3 to o3
Understanding the current state of LLM scaling and the future of AI research...
A majority of recent advancements in AI research—and large language models (LLMs) in particular—have been driven by scale. If we train larger models over more data, we get better results. This relationship can be defined more rigorously via a scaling law, which is just an equation that describes how an LLM’s test loss will decrease as we increase some quantity of interest (e.g., training compute). Scaling laws help us to predict the results of larger and more expensive training runs, giving us the necessary confidence to continue investing in scale.
“If you have a large dataset and you train a very big neural network, then success is guaranteed!” - Ilya Sutskever
For years, scaling laws have been a predictable North Star for AI research. In fact, the success of early frontier labs like OpenAI has even been credited to their religious level of belief in scaling laws. However, the continuation of scaling has recently been called into question by reports1 claiming that top research labs are struggling to create the next generation of better LLMs. These claims might lead us to wonder: Will scaling hit a wall and, if so, are there other paths forward?
This overview will answer these questions from the ground up, beginning with an in-depth explanation of LLM scaling laws and the surrounding research. The idea of a scaling law is simple, but there are a variety of public misconceptions around scaling—the science behind this research is actually very specific. Using this detailed understanding of scaling, we will then discuss recent trends in LLM research and contributing factors to the “plateau” of scaling laws. Finally, we will use this information to more clearly illustrate the future of AI research, focusing on a few key ideas—including scaling—that could continue to drive progress.
Fundamental Scaling Concepts for LLMs
To understand the state of scaling for LLMs, we first need to build a general understanding of scaling laws. We will build this understanding from the ground up, starting with the concept of a power law. Then, we will explore how power laws have been applied in LLM research to derive the scaling laws we use today.
What is a power law?
Power laws are the fundamental concept that underlie LLM scaling. Put simply, power laws just describe a relationship between two quantities. For LLMs, the first of these quantities is the LLM’s test loss—or some other related performance metric (e.g., downstream task accuracy [7])—and the other is some setting that we are trying to scale, such as the number of model parameters. For example, we may see a statement like the following when studying the scaling properties of an LLM.
“With enough training data, scaling of validation loss should be approximately a smooth power law as a function of model size.” - from [4]
Such a statement tells us that a measurable relationship exists between the model’s test loss and the total number of model parameters. A change to one of these quantities will produce a relative, scale-invariant change in the other. In other words, we know from this relationship that increasing the total number of model parameters—assuming other conditions (e.g., having sufficient training data) are met—will result in a decrease of the test loss by predictable factor.
Power law formulation. A basic power law is expressed via the equation below.
The two quantities being studied here are x and y, while a and p are constants that describe the relationship between these quantities. If we plot this power law function2, we get the figure shown below. We provide plots in both normal and log scale because most papers that study LLM scaling use a log scale.
However, the plots provided for LLM scaling do not look like the plot shown above—they are usually flipped upside down; see below for an example.
This is just an inverse power law, which can be formulated as shown below.
The equation for an inverse power law is nearly identically to that of a standard power law, but we use a negative exponent for p. Making the exponent of the power law negative flips the plots upside down; see below for an example.
This inverse power law, when plotted using a log scale, yields the signature linear relationship that is characteristic of most LLM scaling laws. Nearly every paper covered in this overview will produce such a plot to study how scaling up a variety of different factors (e.g., size, compute, data, etc.) impacts an LLM’s performance. Now, let’s take a more practical look at power laws by learning about one of the first papers to study them in the context of LLM scaling [1].
Scaling Laws for Neural Language Models [1]
In the early days of language models, we did not yet understand the impact of scale on performance. Language models were a promising area of research, but the current generation of models (e.g., the original GPT) at that time had limited capabilities. We had yet to discover the power of larger models, and the path towards creating better language models was not immediately clear. Is the shape of the model (i.e., the number and size of layers) important? Does making a model larger help it to perform better? How much data is needed to train these larger models?
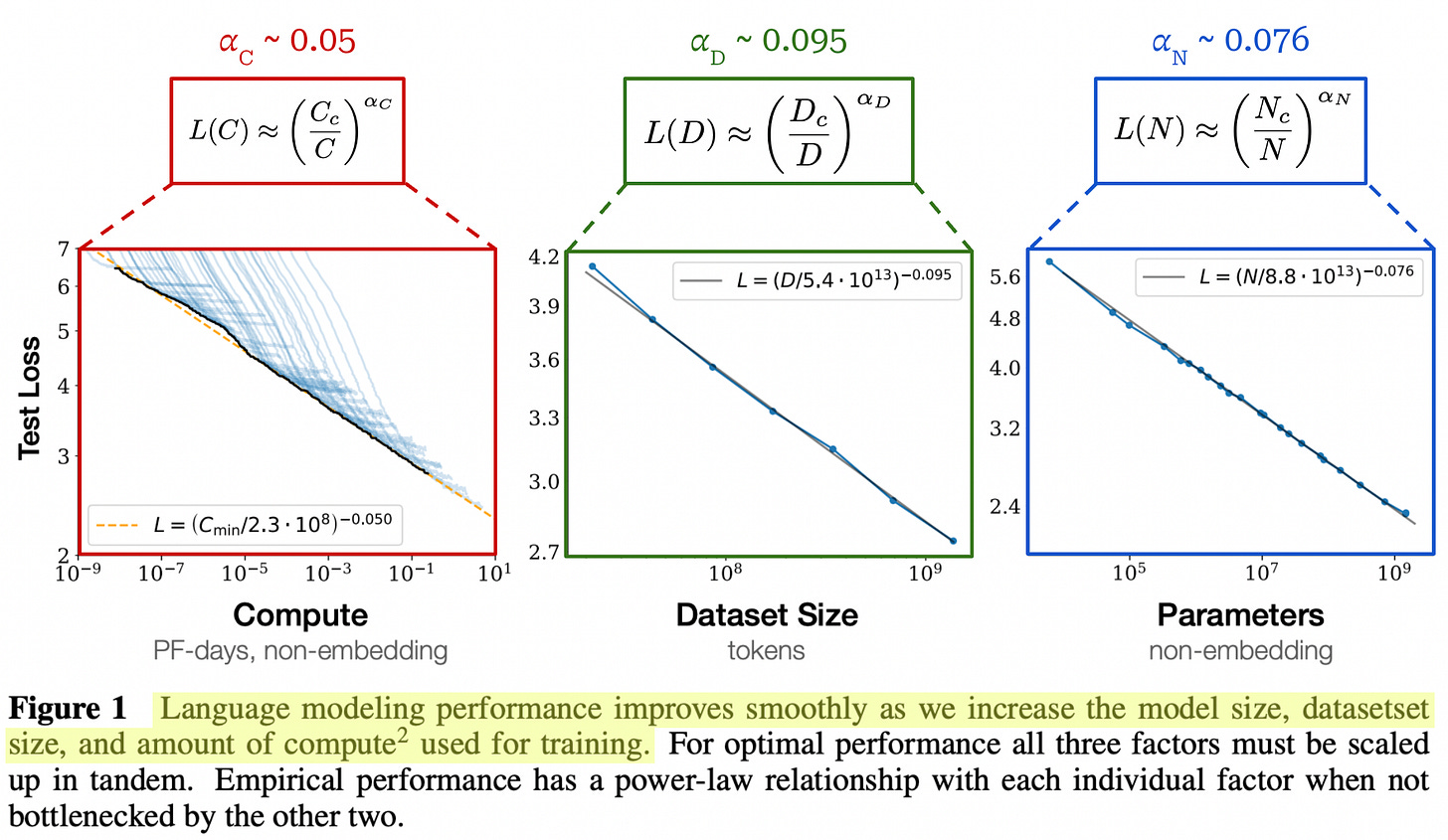
“The loss scales as a power-law with model size, dataset size, and the amount of compute used for training, with some trends spanning more than seven orders of magnitude.” - from [1]
In [1], authors aim to answer these questions by analyzing the impact of several factors—such as model size, model shape, dataset size, training compute, and batch size—on model performance. From this analysis, we learn that LLM performance improves smoothly as we increase:
The number of model parameters.
The size of the dataset.
The amount of compute used for training.
More specifically, a power law relationship is observed between each of these factors and the LLM’s test loss when performance is not bottlenecked by the other two factors.
Experimental setup. To fit their power laws, authors pretrain LLMs with sizes up to 1.5B parameters over subsets of the WebText2 corpus, containing anywhere from 22M to 23B tokens. All models are trained using a fixed context length of 1,024 tokens and a standard next token prediction (cross-entropy) loss. The same loss is measured over a hold-out test set and used as our primary performance metric. This setup matches the standard pretraining setup for most LLMs.
Power laws for LLM scaling. The performance of LLMs trained in [1]—in terms of their test loss on WebText2—is shown to steadily improve with more parameters, data, and compute3. These trends span eight orders of magnitude in compute, six orders of magnitude in model size, and two orders of magnitude in dataset size. The exact power law relationship and the equations that are fit to each of them are provided in the figure above. Each of the equations here are very similar to the inverse power law equation that we saw before. However, we set a = 1 and add an additional multiplicative constant inside of the parenthesis4.
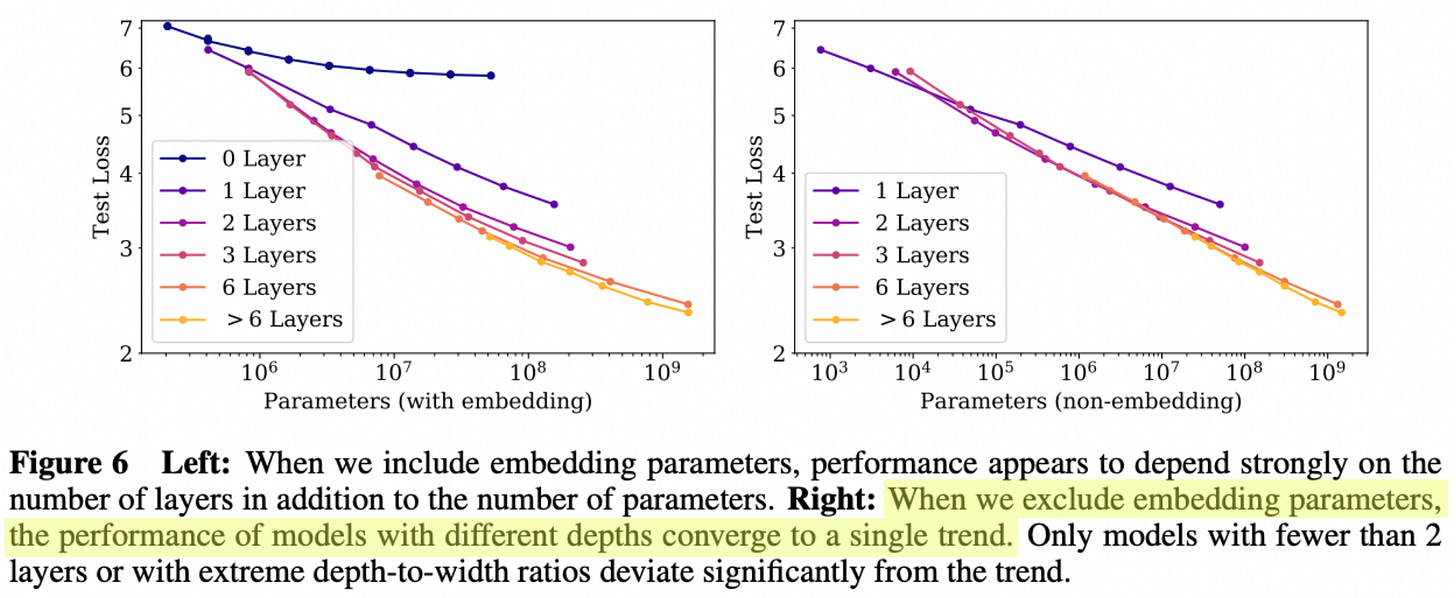
Authors in [1] note one small detail that is necessary to properly fit these power laws. We do not include positional or token embeddings when counting the total number of model parameters, which yields cleaner scaling trends; see below.
These power laws are only applicable if training is not bottlenecked by the other factors. So, all three of these components—model size, data, and compute—should be scaled up simultaneously for optimal performance. If we scale up any of these components in isolation, we will reach a point of diminishing returns.
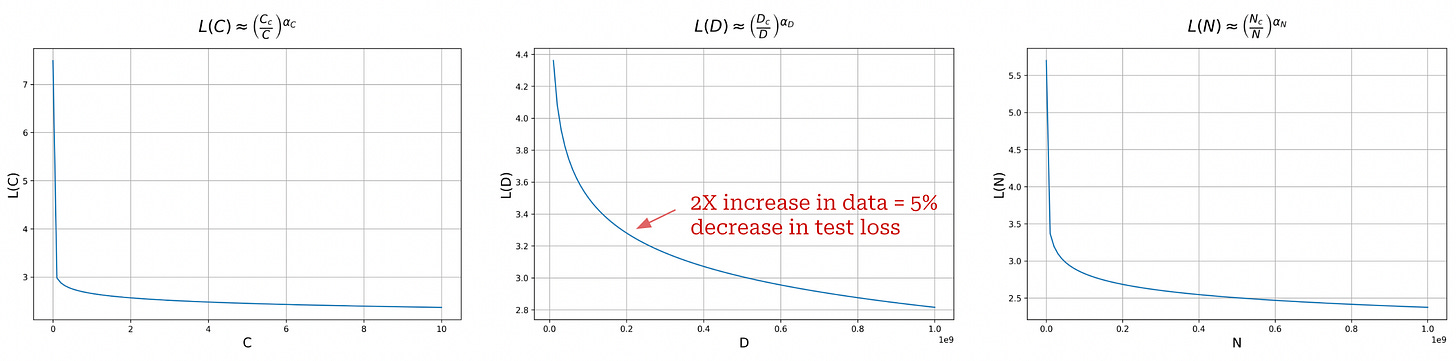
What do power laws tell us? Although the power law plots provided in [1] look quite promising, we should notice that these plots are generated using a log scale. If we generate normal plots (i.e., without log scale), we get the figures below, where we see that the shape of the power law resembles an exponential decay.
Such a finding may seem counterintuitive given a lot of the online rhetoric around scaling and AGI. In many cases, it seems like the intuition we are being fed is that the quality LLMs improves exponentially with logarithmic increases in compute, but this is not the case whatsoever. In reality, increasing the quality of an LLM becomes exponentially more difficult with scale.
Other useful findings. Beyond the power laws observed in [1], we also see that the other factors that are considered, such as model shape or architecture settings, have minimal influence on model performance; see above. Scale is by far the largest contributing factor for creating better LLMs—more data, compute, and model parameters yields a smooth improvement in the LLM’s performance.
“Larger models are significantly more sampleefficient, such that optimally compute-efficient training involves training very large models on a relatively modest amount of data and stopping significantly before convergence.” - from [1]
Interestingly, the empirical analysis in [1] indicates that larger LLMs tend to be more sample efficient, meaning that they reach the same level of test loss with less data relative to smaller models. For this reason, pretraining an LLM to convergence is (arguably) sub-optimal. Instead, we could train a much larger model on less data, stopping the training process far before convergence. Such an approach is optimal in terms of the amount of training compute used but it does not account for inference costs. Practically speaking, we usually train smaller models over more data because smaller models are cheaper to host.
Authors also extensively analyze the relationship between model size and the amount of data used for pretraining, finding that the size of the dataset does not need to be increased as quickly as the model size. An ~8X increase in model size requires a ~5X increase in the amount of training data to avoid overfitting.
The scaling laws discovered in [1] are also replicated on several other datasets, where we see that the same scaling laws hold after adding a fixed offset to the test loss (i.e., to account for the fact that the dataset is different); see above. These results make a compelling case for LLM scaling. We achieve very clear and measurable benefits from training larger models longer and on more data, which created an appetite for pretraining LLMs at a much larger scale.
“These results show that language modeling performance improves smoothly and predictably as we appropriately scale up model size, data, and compute. We expect that larger language models will perform better and be more sample efficient than current models.” - from [1]
Practical Usage of Scaling Laws
The fact that large-scale pretraining is so beneficial presents us with a slight dilemma. The best results are achieved by training massive models over copious amounts of data. However, these training runs are incredibly expensive, which means they also incur a lot of risk. What if we spend $10 million training a model that fails to meet our expectations? Given the expense of pretraining, we cannot perform any model-specific tuning, and we must be sure that the model we train will perform well. We need to develop a strategy for tuning these models and forecasting their performance without spending too much money.
This is where scaling laws come in. So far, we have seen some empirical analysis that was conducted to prove that scaling laws exist, but these scaling laws also have a very practical use case within AI research. In particular, we can:
Train a bunch of smaller models using various training settings.
Fit scaling laws based on the performance of smaller models.
Use the scaling law to extrapolate the performance of a much larger model.
Of course, this approach has limitations. Predicting the performance of larger models from smaller models is difficult and can be inaccurate. Models may behave differently depending on scale. However, various approaches have been proposed to make this more feasible, and scaling laws are now commonly used for this purpose. The ability to forecast the performance of larger models using scaling laws gives us more confidence (and peace of mind) as researchers. Plus, scaling laws provide a simple way to justify investment into AI research.
Scaling and The Age of Pretraining
“This is what has been the driver of all progress we see today—extraordinarily large neural networks trained on huge datasets.” - Ilya Sutskever
The discovery of scaling laws catalyzed much of the recent progress in LLM research. To get better results, we just train increasingly large models on bigger (and better!) datasets. This strategy was followed to create several models within the GPT lineage, as well as most of the notable models from groups other than OpenAI. Here, we will take a deeper look at this progression of scaling research—recently described by Ilya Sutskever as the “age of pretraining”5.
The GPT Lineage: GPT [2], GPT-2 [3], GPT-3 [4], and GPT-4 [5]
The most widely known and visible application of LLM scaling laws was in the creation of OpenAI’s GPT lineage of models. We will primarily focus open earlier models in this lineage—up to GPT-3—because:
The details of these models were shared more openly.
Later models heavily benefitted from advancements in post-training research in addition to scaling up the pretraining process.
We will also cover some of the known scaling results from models like GPT-4.
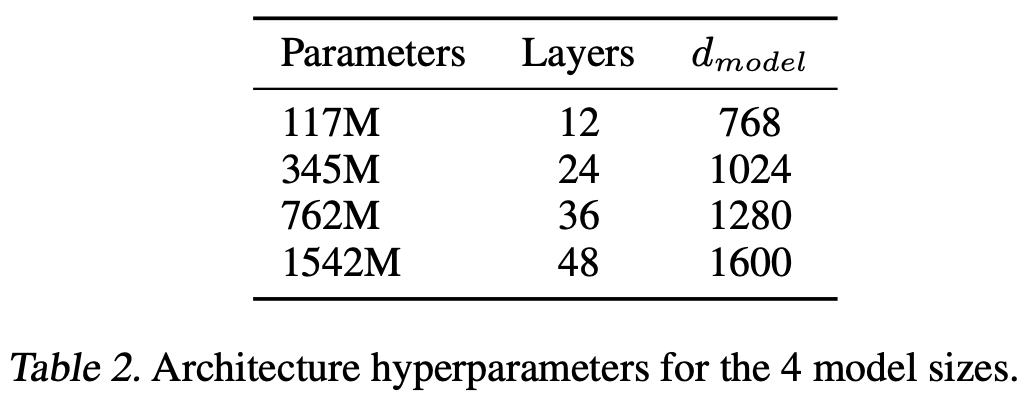
The original GPT model [2] was actually quite small—12 layers and 117M parameters in total. This model is first pretrained over BooksCorpus, a dataset that contains the raw text of ~7,000 books. Then, we finetune the model to solve a variety of different downstream tasks by using a supervised training objective and creating a separate classification head for each task; see above. This paper was one of the first to perform large-scale, self-supervised pretraining of a decoder-only transformer, which led to a few interesting findings:
Self-supervised pretraining on flat text is incredibly effective.
Using long, contiguous spans of text for pretraining is important.
When pretrained in this manner, a single model can be finetuned to solve a wide variety of different tasks with state-of-the-art accuracy6.
Overall, GPT was not an especially noteworthy model, but it laid some important foundations (i.e., decoder-only transformer and self-supervised pretraining) for later work that explored similar models at a much larger scale.
GPT-2 [3] was proposed shortly after GPT and includes a collection of several models with sizes up to 1.5B parameters; see above. These models share the same architecture as the GPT model and are pretrained using the same self-supervised language modeling objective. However, GPT-2 makes two big changes to the pretraining process compared to GPT:
The models are pretrained on WebText, which is i) much larger than BooksCorpus and ii) created by scraping data from the internet.
The models are not finetuned on downstream tasks. Instead, we solve tasks by performing zero-shot inference7 with the pretrained model.
GPT-2 models fall short of state-of-the-art performance on most benchmarks8, but their performance consistently improves with the size of the model—scaling up the number of model parameters yields a clear benefit; see below.
Authors in [3] also reveal that GPT-2 models—despite their impressive results—still seem to underfit the WebText corpus. From this finding, we can infer that continued scaling of LLM pretraining—in terms of both model and data size—should be beneficial. Although the GPT-2 models were not particularly powerful, the analysis presented by these models provided the confidence we needed to continue scaling and eventually reach an inflection point in AI research.
“A language model with sufficient capacity will begin to learn to infer and perform the tasks demonstrated in natural language sequences in order to better predict them, regardless of their method of procurement.” - from [3]
GPT-3 [4] was a watershed moment in AI research that definitively confirmed the benefit of large-scale pretraining for LLMs. The model has over 175B parameters, making it over 100x larger than the largest GPT-2 model; see below.
Again, GPT-3 uses a decoder-only model architecture that is quite similar to that of prior models, but we pretrain the model over a much larger dataset based upon CommonCrawl. This dataset is ~10x bigger than the prior WebText dataset, and authors in [4] combine the larger pretraining dataset with several other sources of pretraining data, creating a mixture of different corpora; see below.
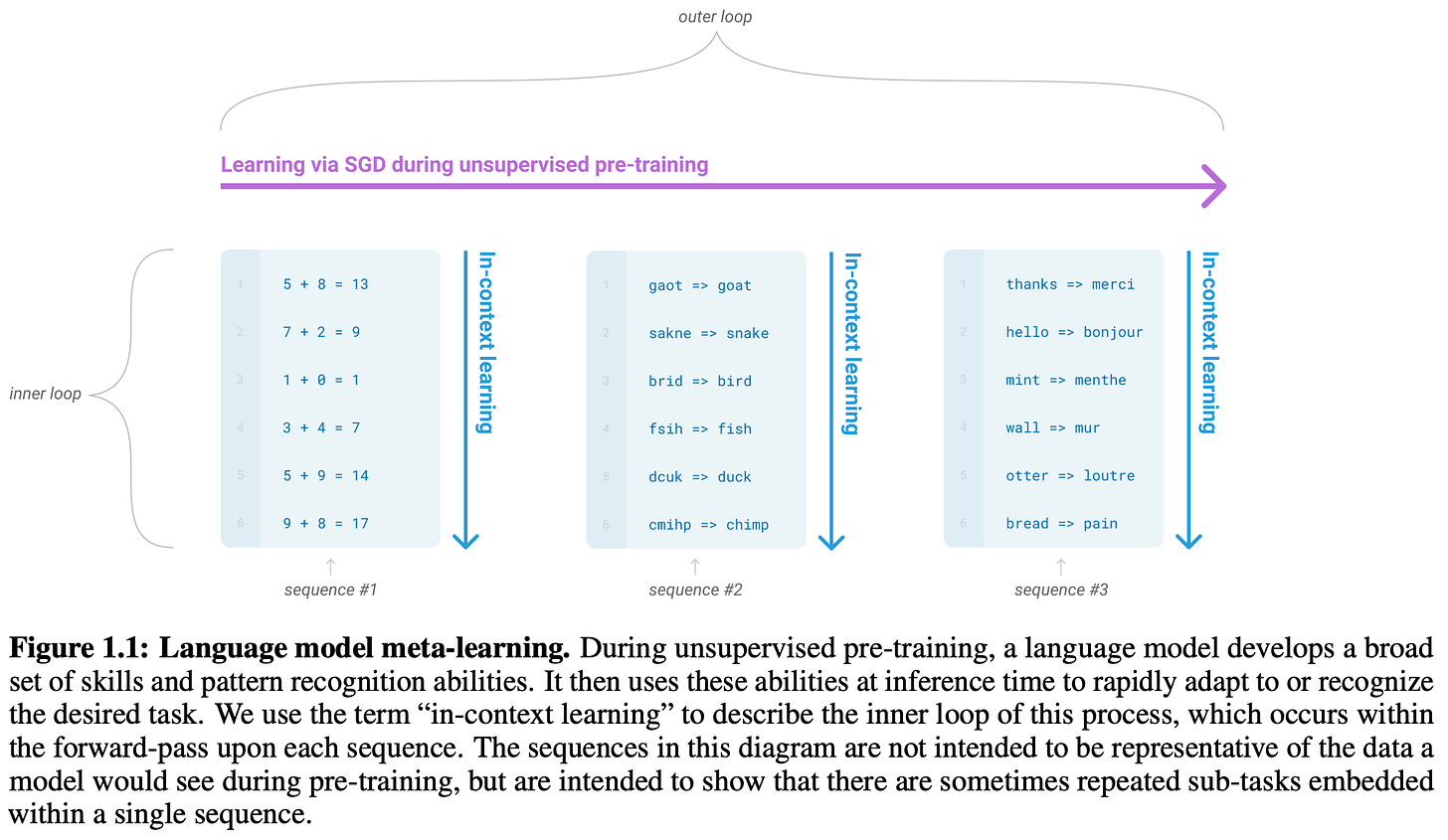
GPT-3 is primarily evaluated in [4] by using a few-shot learning approach. The differences between few-shot prompting (used by GPT-3), zero-shot prompting (used by GPT-2), and finetuning (used by GPT) are illustrated below.
Few-shot learning is a new paradigm in which the LLM learns how to perform a task based upon examples that are placed within its context window. Authors in [4] refer to this concept as “in-context learning”. In this case, the LLM does not actually “learn”—the model’s weights are not updated at all. Rather, the examples in the model’s input are used as context for generating a more accurate output. We see in [4] that GPT-3 is a highly capable few-shot learner, seeming to indicate that in-context learning is an emergent9 ability of larger models; see below.
When GPT-3 is evaluated on various language understanding tasks, we see that using a larger model significantly benefits few-shot learning performance, as shown in the figures below. Larger models make better—and more efficient—use of the information in their context windows relative to smaller models. GPT-3 is able to surpass state-of-the-art performance on several tasks via few-shot learning, and the model’s performance improves smoothly with size.
The fact that a single model was able to perform this well across so many tasks was incredibly impressive at the time. Solving each of these tasks did not require any finetuning or changes to the underlying model—we just had to tweak the model’s prompt. GPT-3 was one of the first true foundation models to be released. This model ushered the next era of AI research and introduced a completely new and intuitive paradigm for interacting with LLMs (i.e., prompting).
Beyond GPT-3. The impressive performance of GPT-3 created an explosion of interest in LLM research, primarily focused upon large-scale pretraining. The next few models released by OpenAI—InstructGPT [8], ChatGPT and GPT-4 [5]—used a combination of large-scale pretraining and new post-training techniques (i.e., supervised finetuning and reinforcement learning from human feedback) to drastically improve LLM quality. These models were so impressive that they even caused the amount of public interest in AI research to skyrocket.
“GPT-4 is a Transformer-based model pre-trained to predict the next token in a document. The post-training alignment process results in improved performance on measures of factuality and adherence to desired behavior.” - from [5]
At this time, OpenAI began to publish fewer details on their research. Instead, new models were just released via their API, which kept the public from learning how these models were created. Luckily, some useful information can be gleaned from the material that OpenAI did publish. For example, InstructGPT [8]—the predecessor to ChatGPT—has an associated paper that documents the model’s post training strategy in detail; see below. Given that this paper also states that GPT-3 is the base model for InstructGPT, we can reasonably infer that this model’s gains in performance are mostly unrelated to scaling up the pretraining process.
Compared to ChatGPT, GPT-4 had a noticeable improvement in capabilities. However, researchers chose to share very few of GPT-4’s technical details. The technical report for GPT-4 [5] simply tells us that:
GPT-4 is transformer-based.
The model is pretrained using next token prediction.
Both public and licensed 3rd party data is used.
The model is finetuned with reinforcement learning from human feedback.
Nonetheless, the importance of scaling is very evident within this technical report. Authors note that a key challenge within this work was developing a scalable training architecture that behaves predictably across different scales, allowing the results of smaller runs to be extrapolated to provide confidence in the larger-scale (and significantly more expensive!) training exercises.
“The final loss of properly-trained large language models is … approximated by power laws in the amount of compute used to train the model.” - from [5]
Large-scale pretraining is incredibly expensive, so we usually only get one chance at getting it right—there is no room for model-specific tuning. Scaling laws play a key role in this process. We can train models using 1,000-10,000x less compute and use the results of these training runs to fit power laws. Then, these power laws can be used to predict the performance of much larger models. In particular, we see in [8] that the performance of GPT-4 is predicted using a power law that measures the relationship between compute and test loss; see below.
This expression looks nearly identical to what we have seen before, but it has an added irreducible loss term to account for the fact that the LLM’s test loss might never reach zero. Once fitted, the scaling law was used to predict the final performance of GPT-4 with very high accuracy; see below for a depiction. Here, we should note that the plot is not generated using a log scale, and we see that the improvement in loss clearly begins to decay with increasing compute!
Authors in [5] also note that the test loss is not an easily interpretable metric and try to predict a variety of other performance metrics. For example, a scaling law is fit to predict the LLM’s pass rate on the HumanEval coding benchmark. First, the problems in HumanEval are split into buckets based on their difficulty. Then, a scaling law is fit to predict the LLM’s pass rate. We see in [5] that the pass rate of GPT-4 can be accurately predicted on HumanEval using this approach based on experiments that require 1,000x less compute; see below.
As we can see, scaling up the pretraining process is valuable. However, large-scale pretraining is also very expensive. Scaling laws make this process more predictable, allowing us to avoid needless or excessive compute costs.
Chinchilla: Training Compute-Optimal Large Language Models [5]
In [1], authors recommend increasing model size faster than the size of the dataset when scaling up LLM pretraining. However, most of the pretraining research after GPT-3 indicated that we should do the opposite. We trained models that were significantly larger than GPT-3—such as the 530B parameter MT-NLG [9] model—but the size of the dataset used to train these models was similar to that of GPT-3; see above. These models did not improve upon the performance of GPT-3, whereas models that used a combination of more parameters with more data (e.g., Gopher [10]) performed much better; see below.
Compute-optimal scaling laws. Inspired by these observations, authors in [6] completely reconsidered the best practices for scaling laws that were originally proposed in [1]. The analysis of scaling laws in [6] was conducted with much larger models, yielding results that are slightly different from before. More specifically, LLMs with sizes ranging from 70M to 17B parameters are trained over datasets with sizes exceeding one trillion tokens; see below.
By training LLMs with many different combinations of model and data size, we can discover a power law that predicts an LLM’s test loss as a function of these factors. From these power laws, we can determine which training settings work best for a given compute budget. Authors in [6] argue that compute-optimal training10 should scale model and data size proportionally. Such a finding reveals that most LLM are undertrained for their size—we would benefit from training existing LLMs over significantly more data. For example, the scaling laws fit in [6] predict that Gopher should have been trained on a 20x larger dataset!
“The amount of training data that is projected to be needed is far beyond what is currently used to train large models.” - from [6]
Chinchilla. The analysis provided in [6] emphasizes the importance of data scale. Large models need to be trained over more data to reach their best performance. To validate this finding, authors train a 70 billion parameter LLM, called Chinchilla. Compared to prior models, Chinchilla is smaller but has a larger pretraining dataset—1.4T training tokens in total. Chinchilla uses the same data and evaluation strategy as Gopher [10]. Despite being 4x smaller than Gopher, Chinchilla consistently outperforms the larger model; see below.
Scaling laws proposed by Chinchilla [6] became a standard in AI research for years afterward. “Chinchilla-optimal” is now a commonly-used term. Even today, after a wide variety of additional scaling research has been published, Chinchilla and its associated scaling laws are referenced constantly.
The “Death” of Scaling Laws
Scaling laws have recently become a popular (and contentious) topic within AI research. As we have seen throughout this overview, scaling has fueled most improvements in AI throughout the age of pretraining. As the pace of model releases and improvements slowed in the latter half of 202411, however, we began to see widespread questioning of model scaling, seeming to indicate that AI research—and scaling laws in particular—could be hitting a wall.
Reuters claims that OpenAI is shifting their product strategy due to hitting a plateau in scaling current methods.
The Information claims that the rate of improvement in GPT models is starting to slow down.
Bloomberg highlights the difficulties being faced by several frontier labs in trying to build AI that is more capable.
TechCrunch claims that scaling is starting to yield diminishing returns.
Time publishes a nuanced essay that highlights various contributing factors to the narrative that AI research is slowing down.
Ilya Sutskever states that “pretraining as we know it will end” during his test of time award speech at NeurIPS’24.
At the same time, many experts are arguing the opposite. For example, Dario Amodei (Anthropic CEO) has said that scaling is “probably… going to continue”, while Sam Altman has continued pushing the narrative that “there is no wall”. In this section, we will add more color to this discussion by providing a grounded explanation of the current state of scaling and various issues that may exist.
Slower Scaling: What does it mean? Why is it happening?
“Both narratives can be true: Scaling is still working at a technical level. The rate of improvement for users is slowing.” - Nathan Lambert
So… is scaling slowing down? The answer is complex and highly dependent upon our exact definition of “slowing down”. So far, the most reasonable response that I’ve seen to this question is that both answers are correct. For this reason, we will not try to answer this question. Instead, we will simply take a deeper look at what exactly the research tells us about this topic so that we can build a more nuanced understanding of the current (and future) state of scaling for LLMs.
What do scaling laws tell us? First, we need to recall the technical definition of a scaling law. Scaling laws define a relationship, based upon a power law, between training compute (or model / dataset size) and the test loss of an LLM. However, the nature of this relationship is often misunderstood. The idea of getting exponential performance improvements from logarithmic increases in compute is a myth. Scaling laws look more like an exponential decay, meaning that we will have to work harder over time to get further performance improvements; see below.
In other words, scaling laws plateau naturally over time. In this way, the “slowdown” we are currently experiencing is arguably an expected part of LLM scaling laws.
“Practitioners often use downstream benchmark accuracy as a proxy for model quality and not loss on perplexity evaluation sets.” - from [7]
Defining performance. How do we measure whether LLMs are improving or not? From the perspective of scaling laws, LLM performance is usually measured via the model’s test loss during pretraining, but the impact of lower test loss on an LLM’s capabilities is unclear. Does lower loss lead to higher accuracy on downstream tasks? Does lower loss cause an LLM to acquire new capabilities? There is a disconnect here between what scaling laws tell us and what we actually care about:
Scaling laws tell us that increasing the scale of pretraining will smoothly decrease the LLM’s test loss.
We care about getting a “better” LLM.
Depending on who you are, your expectations of new AI systems—and the approach that you use to evaluate these new systems—will vary drastically. Average AI users tend to focus upon general chat applications, while practitioners often care about an LLM’s performance on downstream tasks. In contrast, researchers at top frontier labs seem to have high (and very particular) expectations of AI systems; e.g., writing a Ph.D. thesis or solving advanced mathematical reasoning problems. Given that LLMs have such broad capabilities, evaluation is difficult, and there are many lenses from which we can view an LLM’s performance; see below.
Given this drastic variance in model expectations, providing definitive proof that scaling is “working” will always be a struggle. We need a more specific definition of success for scaling laws. If the science tells us that larger models will achieve lower loss, this does not mean that new models will meet everyone’s expectations. A failure to achieve AGI or surpass the capabilities of award-winning human mathematicians is not proof that scaling is not still working at a technical level! Put differently, one could argue that the “slowdown” of scaling is a perception and expectation problem rather than a technical problem with scaling laws.
Data death. To scale up LLM pretraining, we must increase both model and dataset size. Earlier research [1] seemed to indicate that the amount of data was not as important as the size of the model, but we see with Chinchilla [6] that dataset size is equally important. Plus, more recent work argues that most researchers prefer to “overtrain” their models—or pretrain them on datasets that go beyond Chinchilla-optimality in size—to save on inference costs [7].
“Scaling studies usually focus on the compute-optimal training regime... As larger models are more expensive at inference, it is now common practice to over-train smaller models.” - from [7]
All of this research brings us to one simple conclusion—scaling up LLM pretraining will require that we create larger pretraining datasets. This fact forms the basis for one of the key criticisms of LLM scaling laws. Many researchers believe that there may not be enough data available to continue scaling the pretraining process. For context, a large majority of pretraining data used for current LLMs is obtained via web scraping; see below. Given that we only have one internet, finding completely new sources of large-scale, high-quality pretraining data may be hard.

Even Ilya Sutskever has recently made this argument, claiming that i) compute is growing quickly but ii) data is not growing due to reliance upon web scraping. Therefore, he believes that we cannot continue scaling up the pretraining process forever. Pretraining as we know it will end, and we must find new avenues of progress for AI research. In other words, “we have achieved peak data”.
The Next Generation of Scale for Pretraining
Scaling will eventually lead to diminishing returns, and the data-centric argument against the continuation of scaling is both sound and compelling. However, there are still several directions of research that could improve the pretraining process.
Synthetic data. To scale up the pretraining process several orders of magnitude, we will likely need to rely upon synthetically-generated data. Despite worries that over reliance upon synthetic data will lead to diversity issues [14], we are seeing increased—and seemingly successful—usage of synthetic data for LLMs [12]. Additionally, curriculum learning [13] and continued pretraining strategies have led to a variety of meaningful improvements via adjustments to pretraining data; e.g., changing data mixtures or adding instruction data at the end of pretraining.
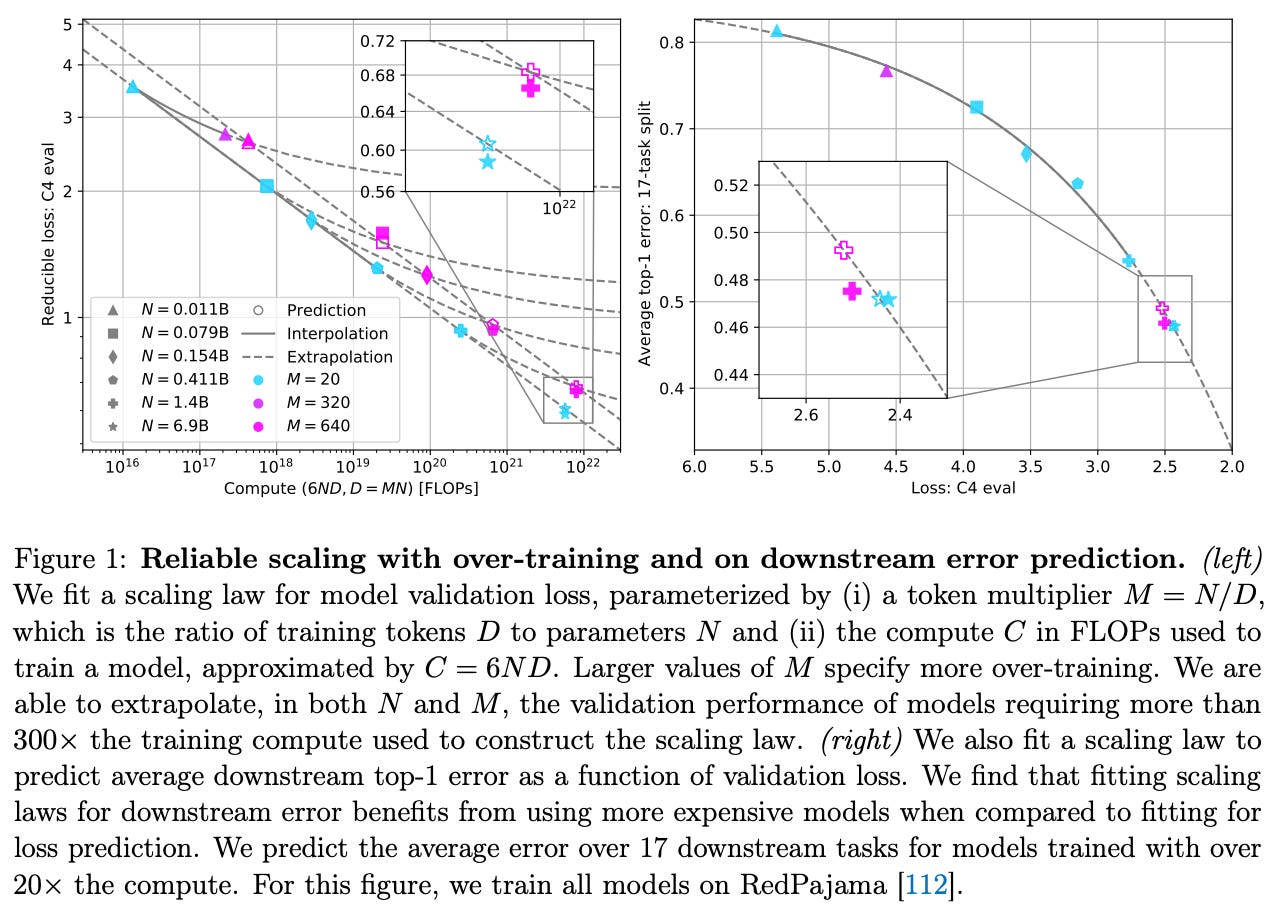
Practical scaling laws. Recent research has attempted to address the limitations of test loss-based scaling laws. For example, authors in [7] define scaling laws that can be used to predict the performance of an LLM on downstream benchmarks from the LLM Foundry; see above. Interpreting these kinds of metrics is much easier for humans. We might not know what a 5% decrease in test loss means, but jumping from 85% to 90% accuracy on our benchmark of interest is usually easy to grasp. Several other works have also explored the idea of using scaling laws to provide more practical and meaningful estimates of LLM performance; e.g., after post training and quantization [16] or during the pretraining process [17].
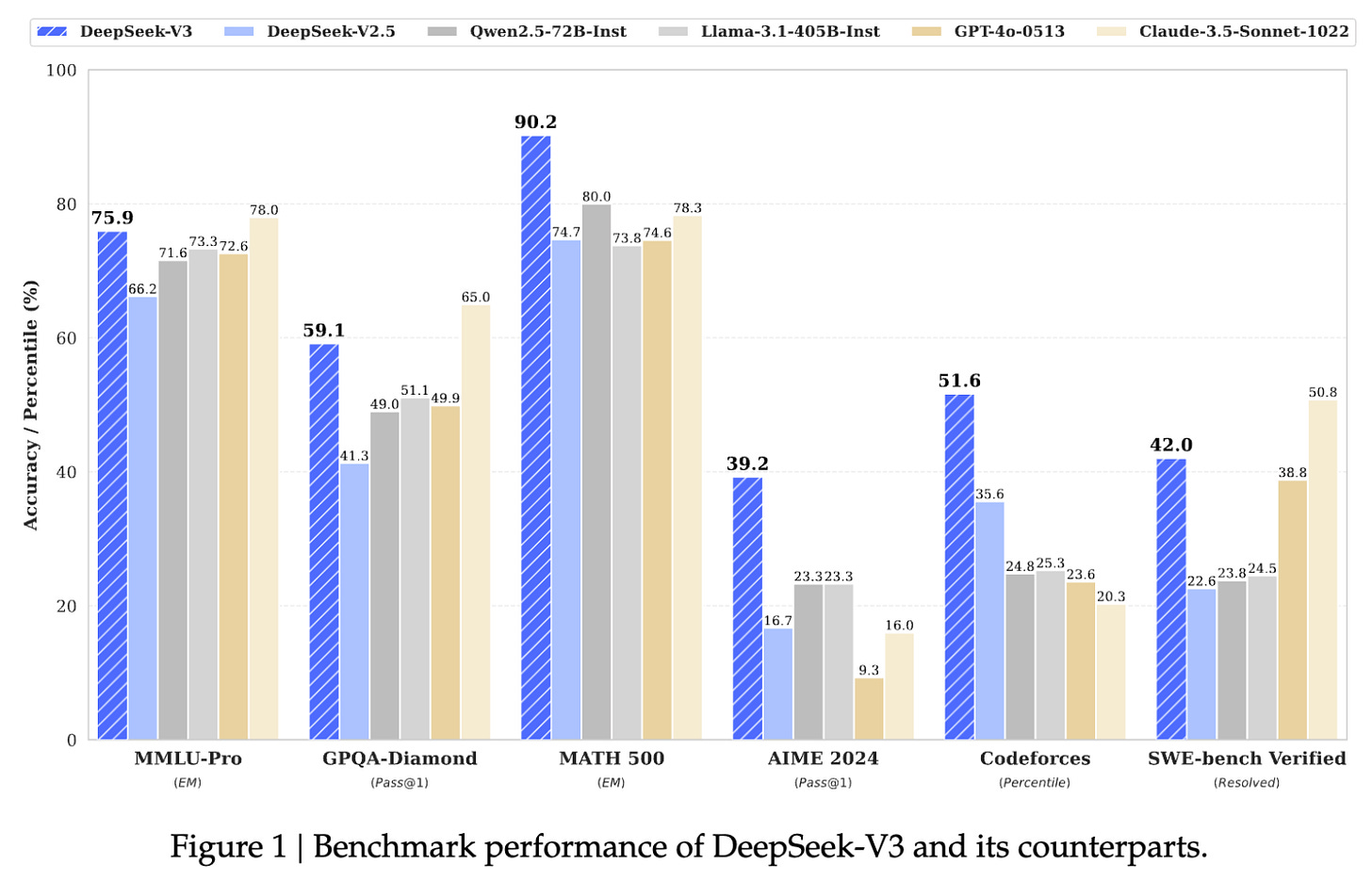
DeepSeek-v3. Despite recent arguments, we are still seeing semi-frequent advancements by scaling the LLM pretraining process. For example, DeepSeek-v3 [18]—a 671B parameter12 mixture-of-experts (MoE) model—was recently released. In addition to being open-source, this model is pretrained on 14.8T tokens of text and surpasses the performance of GPT-4o and Claude-3.5-Sonnet; see below for the model’s performance and here for the license. For reference, LLaMA-3 models are trained on over 15T of raw text data; see here for more details.
The ability to outperform models like GPT-4o is a significant jump for open weights LLMs—even the largest LLaMA models have fallen short of this goal. DeepSeek-v3 adopts a variety of interesting tricks:
An optimized MoE architecture from DeepSeek-v2.
A new auxiliary-loss-free strategy for load balancing the MoE.
A multi-token prediction training objective.
Distillation of reasoning capabilities from a long-chain-of-thought model (i.e., similar to OpenAI’s o1).
The model also undergoes post-training, including supervised finetuning and reinforcement learning from human feedback, to align it to human preferences.
“We train DeepSeek-V3 on 14.8T high-quality and diverse tokens. The pre-training process is remarkably stable. Throughout the entire training process, we did not encounter any irrecoverable loss spikes or have to roll back.” - from [8]
However, the biggest key to DeepSeek-v3’s impressive performance is pretraining scale—this is a massive model trained over an equally-massive dataset! Training such a large model is difficult for a variety of reasons (e.g., GPU failures and loss spikes). DeepSeek-v3 has a surprisingly stable pretraining process and is trained at a reasonable cost by LLM standards; see below. These results indicate that larger-scale pretraining jobs are becoming more manageable and efficient over time.
Increasing scale by an OOM. To continue testing our scaling laws, we must train LLMs that are several orders of magnitude beyond current models. Setting aside our opinions on the utility of scaling, there are still a variety of limitations that stand in the way of training models of this scale. We will need:
Larger compute clusters13.
More (and better) hardware.
Massive amounts of power.
New algorithms (e.g., for larger-scale distributed training, potentially spanning multiple data centers).
Training the next generations of models is not just a matter of securing funding for more GPUs, it is a multi-disciplinary feat of engineering. Such complex efforts take time. For reference, GPT-4 was released in March of 2023, nearly three years—33 months in particular—after the release of GPT-3. It is reasonable to expect a similar timeline (if not longer) for unlocking another 10-100x increase in scale.
“At every order of magnitude scale up, different innovations have to be found.” - Ege Erdil (Epoch AI)
The Future(s) of AI Research
Now that we more deeply understand the state of scaling for pretraining, let’s assume (purely for the purpose of discussion) that pretraining research will hit a sudden wall. Even if model capabilities do not improve at all in the near future, there are a variety of ways in which AI research can continue to rapidly progress. We have already talked about some of these topics (e.g., synthetic data). In this section, we will focus on two topics in particular that are currently popular:
LLM systems / agents.
Reasoning models.
Building Useful LLM Systems
Most LLM-based applications today operate in a single-model paradigm. In other words, we solve tasks by passing that task to a single LLM and directly using the model’s output as the answer to that task; see below.
If we want to improve such a system (i.e., solve harder tasks with higher accuracy), we could simply improve the capabilities of the underlying model, but such an approach is dependent upon the creation of more capable models. Instead, we could go beyond the single-model paradigm by building an LLM-based system that combines several LLMs—or other components—to solve a complex task.
LLM system basics. The goal of an LLM system is to break complex tasks into smaller parts that are easier to solve for an LLM or other module. There are two primary strategies we can use to accomplish this goal (depicted above):
Task decomposition: break the task itself into smaller sub-tasks that can be solved individually and aggregated14 afterwards to form a final answer.
Chaining: solve a task or sub-task by making several sequential calls to an LLM instead of a single call.
These strategies can be used alone or in tandem. For example, assume that we want to build a system to summarize books. To do this, we could decompose the task by first summarizing each chapter of the book. From here, we can either:
Further decompose the task into smaller chunks of text to summarize (i.e., similar to recursive / hierarchical decomposition).
Chain several LLM calls together; e.g., have one LLM extract all important facts or information from the chapter and another LLM produce the chapter summary based on these key facts.
Then, we can aggregate these results by asking an LLM to summarize the concatenated chapter summaries, forming a summary of the full novel. Most complex tasks can be decomposed into simple parts that are easy to solve, which makes such LLM systems very powerful. These systems can become incredibly sophisticated as we perform more extensive decomposition and chaining, making them an interesting (and impactful) area of applied AI research.
Building LLM-based products. Despite the success and popularity of LLMs, the number of practical (and widely-adopted) use cases for LLMs is still very small. The largest use cases for LLMs today are code generation and chat, both of which are relatively obvious applications for LLMs15; see below.

Given that there are so many ripe domains for the application of LLMs, simply building more LLM-based products that are genuinely useful is an important area of applied AI research. We already have access to very capable models, but using these models to build a product worth using is an entirely different problem. Solving this problem requires learning how to build reliable and capable LLM systems.
Agents. The line between LLM systems and agents is blurry because the term “agent” has been overloaded by the AI community. However, the key concept that we should understand is that LLM systems can be expanded in a variety or interesting and meaningful ways. For example, we can augment LLMs by teaching them how to use tools (e.g., calculators, search engines, etc.) when solving a problem; see above. Additionally, we can allow LLMs to execute their own programs or even perform actions for us; e.g., booking a hotel or sending an email. The many modules and tools that can be integrated with an LLM present endless possibilities for building LLM systems that are more capable and useful.
Robustness is one of the biggest roadblocks to building more capable LLM / agent systems. Assume that we have an LLM system that makes ten different calls to an LLM. Additionally, let’s assume that each of these LLM calls have a 95% likelihood of success and that all of the calls need to succeed in order to generate the correct final outputs. Although the individual components of this system are reasonably accurate, the overall system has a success rate of 60%!
As we add more components, this problem becomes exponentially worse, which limits the complexity of LLM / agent systems that we can build. Building more complex systems will require that we drastically improve the robustness of each individual system component. Recent research indicates that robustness can be improved via scaling. However, we can also improve robustness via better meta-generation algorithms; see above. Instead of generating a single output from an LLM, these algorithms use ideas like parallel decoding, (step-level) verification, critiques, and more to obtain a more refined and accurate output from an LLM.
This area of research is rapidly progressing and is likely to become a key driver of progress in AI research; see [20] for an in-depth survey of the topic. As meta-generation algorithms improve, LLMs will become more robust, and we will become capable of building increasingly complex LLM / agent systems.
Reasoning Models and New Scaling Paradigms
A common criticism of early LLMs was that they simply memorized data and had very little reasoning capabilities. However, the inability of LLMs to reason has been largely debunked over the last few years. We have learned from recent research that these models likely had the inherent ability to reason all along, but we have to use the correct prompting or training approach to elicit this ability.
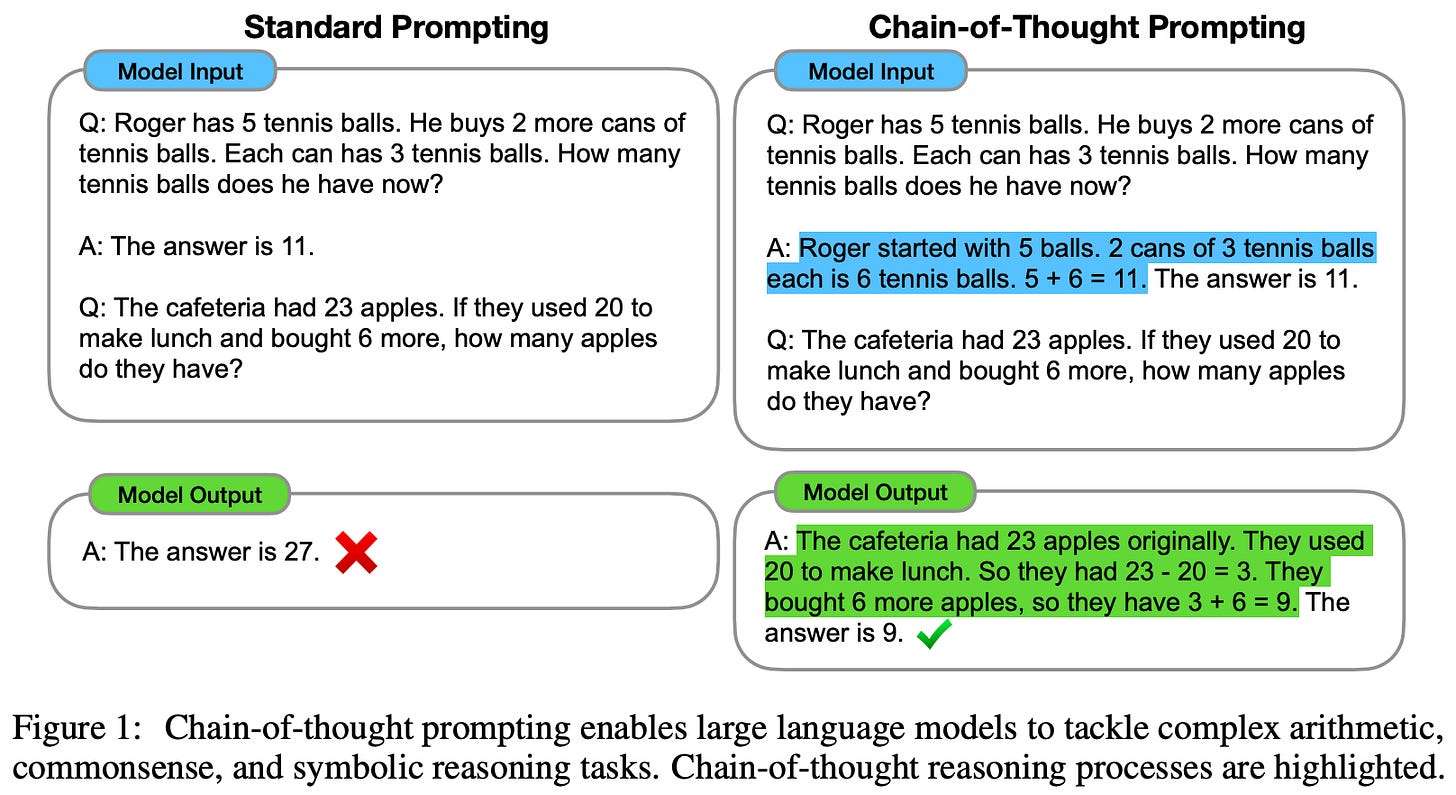
Chain of thought (CoT) prompting [22] was one of the first techniques to demonstrate the reasoning capabilities of LLMs. The approach is simple and prompt-based. We just ask the LLM to provide an explanation for its response prior to generating the actual response; see here for more details. When an LLM generates a rationale that outlines the step-by-step process used to arrive at a response, its reasoning capabilities improve significantly. Plus, this explanation is human-readable and can make the model’s output more interpretable!
The idea of a chain of thought is both generic and powerful. In fact, chains of thought have become the key concept behind improving LLM reasoning capabilities, and we have seen this technique repurposed in many ways:
LLM-as-a-Judge-style evaluation models usually provide scoring rationales prior to generating a final evaluation result [23, 24].
Supervised finetuning and instruction tuning strategies have been proposed for teaching smaller / open LLMs to write better chains of thought [25, 26].
LLMs are commonly asked to reflect upon and critique or verify their own outputs, then revise their output based on this information [12, 27].
Complex reasoning is an active research topic that is quickly progressing. New training algorithms that teach LLMs to incorporate (step-level) verification [28, 29] into their reasoning process have shown promising results, and we will likely continue to see improvements as new and better training strategies emerge.
OpenAI’s o1 reasoning model [21] marks a significant jump in the reasoning capabilities of LLMs. The reasoning strategy used by o1 is heavily based upon chains of thought. Similar to how humans think before responding to a question, o1 will spend time “thinking” before providing a response. Practically speaking, the “thoughts” that o1 generates are just long chains of thought that the model uses to think through a problem, break the problem into simpler steps, try various approaches to solving the problem, and even correct its own mistakes16.
“OpenAI o1 [is] a new large language model trained with RL to perform complex reasoning. o1 thinks before it answers—it can produce a long internal chain of thought before responding to the user.” - from [21]
The details of o1’s exact training strategy are not publicly shared. However, we know that o1 is taught to reason using a “large-scale reinforcement learning” algorithm that is “highly data-efficient” and focuses upon refining the model’s ability to generate useful chains of thought. Based upon public comments from OpenAI researchers and recent rhetoric regarding o1, the model seems to be trained using pure reinforcement learning, which contradicts earlier opinions that o1 may be using some form of tree search at inference time.
As mentioned, the performance of o1 on complex reasoning tasks is impressive. o1 outperforms GPT-4o on nearly all reasoning-heavy tasks; see above. As an example of o1’s reasoning capabilities, the model:
Places in the 89th percentile on competitive programming questions from Codeforces.
Reaches the top 500 students in the US in a qualifier for the USA Math Olympiad (AIME).
Exceeds the accuracy of human PhD candidates on graduate-level physics, biology and chemistry problems (GPQA).
From o1 to o3. One of the most interesting aspects of o1 is that the model’s reasoning capabilities can be improved by using more compute at inference time. To solve problems of increasing complexity, the model can simply generate progressively longer chains of thought; see here for examples. Using more inference-time compute to generate these longer chains of thought yields a smooth increase in the model’s reasoning performance; see below.
“We have found that the performance of o1 consistently improves with more reinforcement learning (train-time compute) and with more time spent thinking (test-time compute).” - from [22]
Similarly, we see in the figure above that o1’s performance improves smoothly as we invest more compute into training via reinforcement learning. This is exactly the approach that was followed to create the o3 reasoning model. The evaluation results for this model were previewed by OpenAI in late 2024, and very few details about o3 have been publicly shared. However, given that this model was released so quickly after o1 (i.e., three months later), o3 is most likely a “scaled up” version of o1 that invests more compute into reinforcement learning.

The o3 model has not yet been released at the time of writing, but the results achieved by scaling o1 are incredibly impressive (even shocking in some cases). The most notable achievements of o3 are listed below:
A score of 87.5% on the ARC-AGI benchmark on which GPT-4o achieves only 5% accuracy. o3 is the first model to exceed human-level performance of 85% on ARC-AGI. This benchmark has been described as a “North Star” towards AGI and has remained unbeaten17 for over five years.
An accuracy of 71.7% on SWE-Bench Verified and an Elo score of 2727 on Codeforces, which ranks o3 among the top 200 human competitive programmers on the planet.
An accuracy of 25.2% on EpochAI’s FrontierMath benchmark, improving upon the previous state-of-the-art accuracy of 2.0%. This benchmark was described by Terence Tao as “incredibly difficult” and likely to be unsolved by AI systems for “several years at least”.
A distilled version of o3, called o3-mini, was also previewed, which performs very well and comes with significant improvements in compute efficiency.
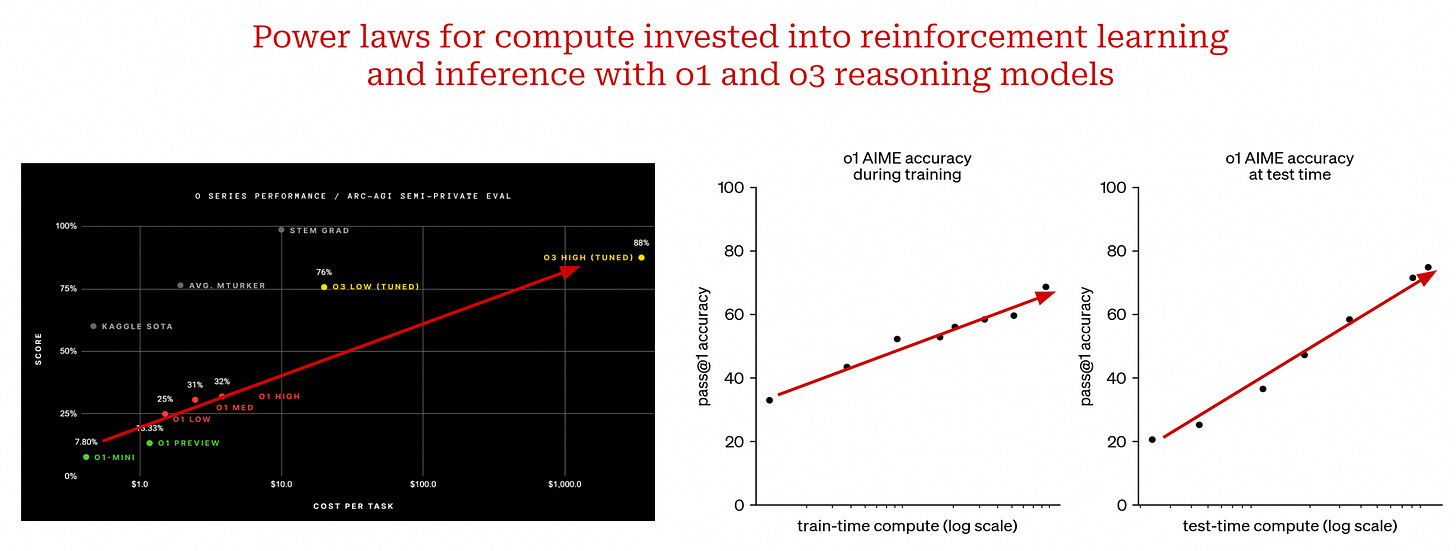
New paradigms for scaling. After reading this overview, many of the plots presented by o1 and o3 (see above) might look pretty familiar—these are log-scale plots where we see a smooth, linear increase in performance with more compute! In other words, we see a clear power law relationship between the performance of these reasoning models and two different quantities:
Training-time (reinforcement learning) compute.
Inference-time compute.
Scaling o1-style models differs from traditional scaling laws. Instead of scaling up the pretraining process, we are scaling the amount of compute invested into post training and inference. This is a completely new scaling paradigm, and the results achieved by scaling reasoning models are great so far. Such a finding shows us that other avenues of scaling—beyond pretraining—clearly exist. With the advent of reasoning models, we have discovered our next hill to climb. Although it may come in a different form, scaling will continue to drive progress in AI research.
Closing Thoughts
We now have a clearer view of scaling laws, their impact on LLMs, and the future directions of progress for AI research. As we have learned, there are many contributing factors to the recent criticism of scaling laws:
The natural decay in scaling laws.
The high variance in expectations of LLM capabilities.
The latency of large-scale, inter-disciplinary engineering efforts.
These issues are valid, but none of them indicate that scaling is not still working as expected. Investments into large-scale pretraining will (and should) continue, but improvements will become exponentially harder over time. As a result, alternative directions of progress (e.g., agents and reasoning) will become more important. As we invest into these new areas of research, however, the fundamental idea of scaling will continue to play a massive role. Whether scaling will continue is not a question. The true question is what we will scale next.
New to the newsletter?
Hi! I’m Cameron R. Wolfe, Deep Learning Ph.D. and Machine Learning Scientist at Netflix. This is the Deep (Learning) Focus newsletter, where I help readers better understand important topics in AI research. If you like the newsletter, please subscribe, share it, or follow me on X and LinkedIn!
Bibliography
[1] Kaplan, Jared, et al. "Scaling laws for neural language models." arXiv preprint arXiv:2001.08361 (2020).
[2] Radford, Alec. "Improving language understanding by generative pre-training." (2018).
[3] Radford, Alec, et al. "Language models are unsupervised multitask learners." OpenAI blog 1.8 (2019): 9.
[4] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.
[5] Achiam, Josh, et al. "Gpt-4 technical report." arXiv preprint arXiv:2303.08774 (2023).
[6] Hoffmann, Jordan, et al. "Training compute-optimal large language models." arXiv preprint arXiv:2203.15556 (2022).
[7] Gadre, Samir Yitzhak, et al. "Language models scale reliably with over-training and on downstream tasks." arXiv preprint arXiv:2403.08540 (2024).
[8] Ouyang, Long, et al. "Training language models to follow instructions with human feedback." Advances in neural information processing systems 35 (2022): 27730-27744.
[9] Smith, Shaden, et al. "Using deepspeed and megatron to train megatron-turing nlg 530b, a large-scale generative language model." arXiv preprint arXiv:2201.11990 (2022).
[10] Rae, Jack W., et al. "Scaling language models: Methods, analysis & insights from training gopher." arXiv preprint arXiv:2112.11446 (2021).
[11] Bhagia, Akshita, et al. "Establishing Task Scaling Laws via Compute-Efficient Model Ladders." arXiv preprint arXiv:2412.04403 (2024).
[12] Bai, Yuntao, et al. "Constitutional ai: Harmlessness from ai feedback." arXiv preprint arXiv:2212.08073 (2022).
[13] Blakeney, Cody, et al. "Does your data spark joy? Performance gains from domain upsampling at the end of training." arXiv preprint arXiv:2406.03476 (2024).
[14] Chen, Hao, et al. "On the Diversity of Synthetic Data and its Impact on Training Large Language Models." arXiv preprint arXiv:2410.15226 (2024).
[15] Guo, Zishan, et al. "Evaluating large language models: A comprehensive survey." arXiv preprint arXiv:2310.19736 (2023).
[16] Xu, Zifei, et al. "Scaling laws for post-training quantized large language models." arXiv preprint arXiv:2410.12119 (2024).
[17] Xiong, Yizhe, et al. "Temporal scaling law for large language models." arXiv preprint arXiv:2404.17785 (2024).
[18] DeepSeek-AI et al. "DeepSeek-v3 Technical Report." https://github.com/deepseek-ai/DeepSeek-V3/blob/main/DeepSeek_V3.pdf (2024).
[19] Schick, Timo, et al. "Toolformer: Language models can teach themselves to use tools." arXiv preprint arXiv:2302.04761 (2023).
[20] Welleck, Sean, et al. "From decoding to meta-generation: Inference-time algorithms for large language models." arXiv preprint arXiv:2406.16838 (2024).
[21] OpenAI et al. “Learning to Reason with LLMs.” https://openai.com/index/learning-to-reason-with-llms/ (2024).
[22] Wei, Jason, et al. "Chain-of-thought prompting elicits reasoning in large language models." Advances in neural information processing systems 35 (2022): 24824-24837.
[23] Liu, Yang, et al. "G-eval: Nlg evaluation using gpt-4 with better human alignment." arXiv preprint arXiv:2303.16634 (2023).
[24] Kim, Seungone, et al. "Prometheus: Inducing fine-grained evaluation capability in language models." The Twelfth International Conference on Learning Representations. 2023.
[25] Ho, Namgyu, Laura Schmid, and Se-Young Yun. "Large language models are reasoning teachers." arXiv preprint arXiv:2212.10071 (2022).
[26] Kim, Seungone, et al. "The cot collection: Improving zero-shot and few-shot learning of language models via chain-of-thought fine-tuning." arXiv preprint arXiv:2305.14045 (2023).
[27] Weng, Yixuan, et al. "Large language models are better reasoners with self-verification." arXiv preprint arXiv:2212.09561 (2022).
[28] Lightman, Hunter, et al. "Let's verify step by step." arXiv preprint arXiv:2305.20050 (2023).
[29] Zhang, Lunjun, et al. "Generative verifiers: Reward modeling as next-token prediction." arXiv preprint arXiv:2408.15240 (2024).
The two primary reports are from The Information and Reuters.
We use the following settings to generate the plot: a = 1, p = 0.5, and 0 < x < 1.
Compute is defined in [1] as 6NBS, where N is the number of model parameters, B is the batch size used during training, and S is the total number of training steps.
This extra multiplicative constant does not change the behavior of the power law. To understand why this is the case, we must understand the definition of scale invariance. Because power laws are scale invariant, the fundamental characteristics of a power law are the same even when we scale up or down by a certain factor. The behavior observed will be the same at any scale!
This description was from Ilya’s test of time award for this paper at NeurIPS’24.
Although this might seem obvious now, we should remember that most NLP tasks at the time (e.g., summarization and QA) had entire areas of research devoted to them! Each of these tasks had associated task-specific architectures that were specialized in performing that task, and GPT was a single generic model that could outperform most of these architectures across several different tasks.
This means that we just describe each task in the LLM’s prompt and use the same model to solve different tasks—only the prompt changes between tasks.
This is to be expected because these models use zero-shot inference and are not finetuned at all on any of the downstream tasks.
By an “emergent” ability, we mean a skill possessed by the LLM that only emerges after a certain scale has been reached (e.g., a sufficiently large model).
Here, we define “compute-optimal” as the training setting that yields the best possible performance—in terms of test loss—at a fixed training compute cost.
best performance at a fixed compute cost
For example, Anthropic has continually pushed back their release of Claude 3.5 Opus, Google has only released the flash variant of Gemini-2, and OpenAI only released GPT-4o in 2024 (until o1 and o3 were released in December), which was arguably not significantly more capable than GPT-4.
Only 37 billion of these parameters are active during inference for a single token.
For example, xAI has recently built a new datacenter with 100,000 NVIDIA GPUs in Memphis, while Anthropic leadership has voiced a desire to increase their compute spend by up to 100x over the next few years.
The aggregation step can be implemented in a variety of ways. For example, we can manually aggregate responses (e.g., via concatenation), use an LLM, or pretty much anything in between!
This is not because these tasks are simple. Both code generation and chat are hard to solve, but they are (arguably) fairly obvious applications for LLMs.
OpenAI has chosen to hide these long chains of thought from the users of o1. The argument behind this choice is that these rationales provide insight into the model’s though process that can be used to debug or monitor the model. However, the model should be allowed to express its pure thoughts without any of the safety filtering that is necessary for user-facing model outputs.
Currently, ARC-AGI is technically still unbeaten because o3 exceeds the compute requirement for the benchmark. However, the model still achieves an accuracy of 75.7% using a lower compute setting.


































Perfect article, thank you so much for your writing and amazing insights!
Hi Cameron,
Thanks for the awesome article
You might be interested in this https://arxiv.org/abs/2501.04682 article for the o1/o3 section