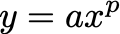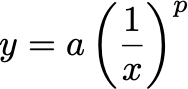Language Model Scaling Laws and GPT-3
Understanding why LLMs like GPT-3 work so well...
Language models (LMs) are incredibly generic–they take text as input and produce text as output. Recent research has revealed that this generic text-to-text structure can be exploited to solve a variety of tasks without task-specific adaptation (i.e., no fine-tuning or architectural modifications) by using prompting techniques to perform accurate zero and few-shot inference. Put simply, we can pre-train the LM over a large, unlabeled text corpus (using a language modeling objective), then ask the LM via textual prompts to solve a problems. In this way, the pre-trained model can easily be repurposed for solving different problems.
Although LMs hold incredible potential as task-agnostic foundation models, initial attempts at transferring pre-trained LMs to solving downstream tasks (e.g., GPT and GPT-2 [4, 5]) did not work well. Within this overview, we will learn how recent research has built upon these initial attempts and created LMs that achieve much better task-agnostic performance. The key finding within this line of work is that LMs become much more powerful as you scale them up.
More specifically, we will learn that large LMs (LLMs) are (i) more sample efficient than their smaller counterparts and (ii) more capable of task-agnostic transfer to downstream tasks. Interestingly, the performance of these LLMs follows predictable trends with respect to various factors (e.g., model size and the amount of training data). The empirical observation of these trends eventually led to the creation of GPT-3, a 175 billion parameter LLM that far surpasses the task-agnostic performance of its predecessors and even outperforms state-of-the-art, supervised deep learning techniques on certain tasks.
Background
Most prerequisite information needed to understand LMs has already been covered in one of my prior posts. These prerequisites include the language modeling objective, decoder-only transformer models, and how these ideas can be combined to generate powerful foundation models. Check out the link below to learn more.
I will give a quick overview of these ideas here, as well as explain a few additional concepts that are useful for understanding LLMs like GPT-3.
language modeling at a glance
Modern LMs use generic pre-training procedures to solve a wide variety of tasks without the need for downstream adaptation (i.e., no architectural modifications, fine-tuning etc.). Using a large corpus of unlabeled text, we pre-train our LM using a language modeling objective that (i) samples some text from our corpus and (ii) tries to predict the next word that occurs. This is a form of self-supervised learning, as we can always find the ground truth next word by simply looking at the data in our corpus; see below.
architecture. Modern LMs use decoder-only transformer architectures, which apply a sequence of layers consisting of masked self-attention and feed forward transformations to the model’s input. Masked self-attention is used instead of bidirectional self-attention, as it prevents the model from “looking forward” in a sequence to discover the next word.
Beyond these decoder-only layers, the LM architecture contains embedding layers that store vectors corresponding to all possible tokens within a fixed-size vocabulary. Using these embedding layers, raw text can be converted into a model-ingestible input matrix as follows:
Tokenize raw text into individual tokens (i.e., words or sub-words)
Lookup the corresponding embedding vector for each input token
Concatenate token embeddings, forming a matrix/sequence of token vectors
Add position (and other) embeddings to each token
See the figure below for an illustration of this process.
The differentiation between embedding and decoder-only layers within the LM is important to understand. For example, some later work in this overview will study the number of parameters within the underlying LM by excluding parameters in the embedding layer and only counting those contained within decoder-only layers.
adaptation. By pre-training LMs over a large corpus, we obtain a model that can accurately predict the next token given a sequence of tokens as context. But, how do we use such a model to solve language understanding tasks like sentence classification and language translation?
For modern LMs, the answer to this question is actually quite simple–we don’t change the LM at all. Instead, we exploit the generic nature of the model’s text-to-text input-output structure by providing textual “prompts” to the model, such as:
“Translate this sentence to English: <sentence> =>”
“Summarize the following document: <document> =>”.
Given these problem-solving prompts, a good LM should output a textual sequence that solves the problem for us! For problems in which we must choose from a fixed set of solutions (i.e., multiple choice or classification) instead of just generating text, we can use the LM to measure the probability of generating each potential solution and choose the most probable solution.
main takeaway. The crux of modern LLMs is that we can use language model pre-training as a tool for creating generic foundation models that solve various problems without the need to adapt or fine-tune the model. Although prior LMs like GPT and GPT-2 [4, 5] perform poorly compared to fine-tuned or supervised language understanding techniques, such a learning framework is quite promising and—as we will see with GPT-3–can even perform quite well when the underlying LM becomes much larger.
power laws
This overview will contain several references to the idea of power laws. For example, a paper may make a statement like the following:
“The LM’s test loss varies as a power law with respect to the number of model parameters”.
This sentence simply tells us that a relationship exists between two quantities–the loss and the number of model parameters–such that a change in one quantity produces a relative, scale-invariant change in the other.
To make this a bit more concrete, a power law is expressed via the following equation.
Here, the two quantities we study are x and y, while a and p dictate the shape/behavior of the power law between these quantities. Plotting this power law (with a = 1, p = 0.5, and 0 < x, y < 1) yields the illustration below, where converting both axes to a log scale produces a signature linear trend that is characteristic of power laws.
Power laws simply tell us that one quantity varies as a power of another quantity. The work we will see in this overview considers an inverse version of a power law, as shown below.
Notably, this is the same equation as before with a negative exponent for p. This negative exponent yields the graph shown below, where one quantity decreases as the other increases.
We will encounter power laws that resemble the figure above within our analysis of LMs. Namely, the LM loss tends to decrease according to a power law with respect to several different factors, such as the model or dataset size. We will expand upon this more in later sections.
other useful details
In addition to the core ideas behind language modeling, there are a few additional concepts that might be helpful to know moving forward.
distributed training. The main idea of the papers within this overview is scaling up models like GPT and GPT-2 [4, 5] to make them better. As our models get bigger and bigger, however, training becomes more difficult due to an increase in computational and memory overhead. To help with this, we can leverage distributed training techniques, which use more hardware (i.e., more servers/GPUs) to make large-scale training processes more tractable and efficient.
There are a couple of different ways to distribute the training process for neural networks. One of these techniques is data parallel training, in which we:
Take a large mini-batch
Split this mini-batch into several, smaller sub-batches
Perform the computation related to each sub-batch in parallel on a different GPU
Accumulate the sub-batch results from each GPU into a centralized model update
Such an approach enables improved training efficiency by parallelizing model computation over a large mini-batch across several GPUs.
Somewhat differently, we can perform model-parallel training, which splits the model itself (i.e., instead of the mini-batch) across multiple GPUs. For example, we can send each layer of a model–or even smaller portions of each layer–to a separate GPU. Practically, this means that the forward pass is spread across several devices or GPUs that each contain a small portion of the underlying model. Such an approach enables larger models to be trained (i.e., because each GPU only stores a small portion of the model!) and can yield improvements in training efficiency via smart pipelining and parallelization of the model’s forward pass.
For the purposes of this overview, we just need to know that we can leverage distribution across many GPUs to make LLM training more tractable and efficient. Data and model parallel training are examples of popular distributed training techniques. Many considerations and alternative methodologies for distributed training exist–this is an entire field of study within deep learning that yields a lot of awesome, practical results.
To learn more, I would recommend checking out the following articles:
critical batch size. Given that using large batches for data parallel training can benefit computational efficiency, we should just make our batches as big as possible, right? Well, this isn’t quite correct, as (i) larger batches might deteriorate model performance and (ii) increasing the batch size increases compute costs and requires extra hardware. Put simply, increasing the batch size too much has diminishing returns; see below.
With this in mind, we might begin to wonder: what’s the best batch size to use? This question was answered empirically with the proposal of the critical batch size in [3]. This work uses a metric called the gradient noise scale to estimate the largest useful batch size across a variety of domains. Beyond this critical batch size, we start to see diminishing returns in terms of performance and compute efficiency. Because adopting different batch sizes can impact the efficiency and quality of training, some work–as we will see in this overview–adopts the critical batch size as a standard practice for resource efficient training.
Beam search. LM’s solve problems by outputting a textual sequence in response to a prompt. These sequences can be generated autoregressively by continually predicting the next word, adding this word to the input prompt, predicting another word, and so on; see the figure below.
However, the greedy approach of continually predicting the most probable next word is not optimal! This is because the probability of a sequence of tokens (assuming each token is generated independently) is the product of each word’s conditional probability given preceding tokens (i.e., due to the chain rule of probability). Greedily choosing the most probable next token might not maximize this probability; e.g., initially choosing a low probability token might subsequently lead to higher probability tokens in the rest of the sequence.
Instead of testing all combinations of possible output tokens to find the best output sequence, we can find an approximate solution with beam search. The idea behind beam search is simple: instead of choosing the most probable next token at each step, choose the top-k most probable generations, maintain a list of possible output sequences based on these top choices, then select the most probable of these sequences at the end.
Publications
We will now overview publications that predict [1] and empirically validate [2] the incredible practical utility of LLMs like GPT-3. From these publications, we will gain a better understanding of why LLMs are so powerful and see extensive analysis of their performance in practical applications.
Scaling Laws for Neural Language Models [1]
GPT and GPT-2 [4, 5] showed us that LMs have incredible potential as generic foundation models, but their performance when transferring to downstream tasks still leaves a lot to be desired. Thus, we might begin to ask: how can we make these models better?
In [1], authors study one potential direction for making LMs more powerful–scaling them up. In particular, they train a bunch of decoder-only LMs and analyze their test loss (i.e., cross-entropy language modeling loss over a hold-out test set) as a function of several factors, including:
Model size
Amount of data
Amount of training compute
Batch size
Architectural details (i.e., model width/depth, number of attention heads, etc.)
Context length (i.e., number of tokens used to predict the next token)
This analysis reveals several fundamental properties of LM training behavior. For example, tweaking architectural details has minimal impact on LM performance if the total number of parameters is fixed. However, the LM’s test loss follows a power law with respect to model size, data size, and the amount of training compute across several orders of magnitude; see below.
To make this a bit more clear, the authors in [1] consider three main factors: model size (N), data size (D), and the amount of training compute (C). To study scaling behavior with respect to any one of these factors, we (i) make sure that the other two factors are sufficiently large (i.e., so they aren’t a bottleneck to performance), then (ii) measure the LM’s test loss over a wide range of values for the factor we are studying. For example, to study the scaling properties of C, we make sure the model and dataset are sufficiently large, then measure LLM performance across different settings of C. We will now consider each of these factors individually.
model size. To study scaling properties with respect to model size, authors train different LM to convergence over the full dataset from [1]–WebText2, an extended version WebTest from GPT-2 [2] that is ~10X larger. Then, by adopting several LMs with different numbers of total parameters, we can obtain the figure shown below.
By plotting the LM’s test loss as a function of the total number of parameters within the decoder-only layers (i.e., excluding all parameters in the embedding layer), we can see that LM loss follows a smooth power law with respect to N. In other words, increasing the size of the LM yields a steady improvement in its performance.
data and compute. To study how LM performance scales with the amount of training data, authors of [1] adopt a sufficiently-large LM and perform separate training trails over differently-sized datasets. For each trial, the model is trained until the test loss begins to increase, an indication of overfitting. Again, this analysis shows us that test loss decreases according to a power law with respect to the size of the dataset; see above.
We see a very similar trend when varying the amount of training compute, defined as C = 6NBS for batch size B and number of training iterations S. Given a sufficiently-large dataset and fixed batch size B, we can scan over numerous LM sizes N to obtain the result shown above. Here, we see that the optimal results for each compute budget C are achieved using different combinations of N and S, but the best LM loss decreases according to a power law with respect to the amount of training compute.
Going further, we can see from these results that LM sample efficiency (i.e., how many samples it takes for the model to perform well) improves with increasing N. To show this more clearly, authors of [1] analyze the performance of different-sized LMs with respect to the total number of samples observed during training, yielding the plot shown below. Here, we can clearly see LM performance improves more quickly as the models become larger.
pairwise scaling laws. Beyond the power laws observed by analyzing N, D, and C in isolation, varying pairs of these factors simultaneously can also yield predictable behavior; e.g., by jointly varying N and D we can obtain the plot shown below. Here, we observe that (i) larger models begin to overfit on smaller datasets and (ii) LM loss follows a strict power law with respect to N given a sufficiently large dataset.
At a high level, this tells us that we must make the dataset larger in order to avoid overfitting when we increase the size of the underlying LM. However, authors in [1] find that scaling the data size sub-linearly (i.e., proportional to N^0.74 specifically) is sufficient to avoid overfitting.
Takeaways. Though we have discussed the power laws outlined in [1] at a high level, the actual publication makes these laws quite concrete and even proposes an accurate predictive framework for the test loss of any LM. For simplicity, we avoid these details here, instead focusing on the following takeaways for training LMs.
If we are increasing the scale of LM training, we should:
Invest most of the extra compute into an increased model size (i.e., larger models are more sample efficient)
Increase the size of the dataset (but not as much as the model size) to avoid overfitting.
Slightly increase the batch size (i.e., according to the critical batch size [3]).
Stop training the model significantly short of convergence to optimize the use of training compute.
The power laws observed in [1] continue seemingly unimpeded for several orders of magnitude. Although this scaling will eventually reach a limit, it nonetheless shows that (properly) increasing the scale of LM training yields measurable performance benefits, hinting that exploring LLMs (like GPT-3) could prove to be incredibly beneficial.
“Our results strongly suggest that larger models will continue to perform better, and will also be much more sample efficient than has been previously appreciated. Big models may be more important than big data.” - from [1]
Language Models are Few-Shot Learners [2]
Prior work on GPT and GPT-2 [4, 5] began to reveal the utility of general purpose LMs for solving textual understanding tasks. However, these models still had limitations:
GPT was not fully task-agnostic (i.e., required task-specific fine-tuning)
GPT-2 performed far worse than supervised state-of-the-art in the zero-shot regime
Existing work provides a “proof of concept” that LMs could remove the need for task specification by performing zero/few-shot, task-agnostic inference. However, the poor performance of LMs relative to supervised techniques makes them less practical. Luckily, the power laws observed within [1] provide hope that larger LMs (i.e., LLMs) could narrow the gap between task-agnostic and task-specific/supervised performance.
Moving in this direction, GPT-3, which shares the same decoder-only architecture as GPT-2 (aside from the addition of some sparse attention layers [6]), builds upon the size of existing LMs by several orders of magnitude. In particular, it is an LLM with over 175 billion parameters (i.e., for reference, GPT-2 [5] contains 1.5 billion parameters); see below.
With GPT-3, we finally begin to see promising task-agnostic performance with LLMs, as the model’s few-shot performance approaches that of supervised baselines on several tasks. Similar to GPT-2, authors pre-train the LLM using a language modeling objective, but they adopt a larger dataset based upon a filtered version of CommonCrawl and some additional, high-quality corpora. The breakdown of the full dataset used for pre-training is shown below.
Pre-training with GPT-3 is conducted similarly to GPT-2, but the model is trained for much longer. To make the training process computationally feasible, the authors adopt a model parallel distributed training approach that distributes portions of each LM layer across separate GPUs. Because each GPU only stores a small portion of the full model, training can be conducted without exceeding memory constraints.
The learning process of GPT-3 has two components: un/self-supervised pre-training and in-context learning. These two components are illustrated in the figure below.
Put simply, we first pre-train the general purpose LLM over a large unsupervised text corpus, then guide this model to solve downstream tasks using in-context learning. This in-context learning process can be performed via task-specific fine-tuning (as in GPT) or even using techniques like few-shot learning that require no gradient updates to the LM. The difference between fine-tuning and different variants of zero, one, and few-shot learning is depicted below.
Unlike prior variants, GPT-3 is evaluated solely using zero and few-shot learning techniques. The authors do not adapt or fine-tune the model to any of the downstream datasets used for evaluation. Rather, they pre-train this incredibly large model over a massive text corpus and study whether in-context learning can be accurately performed using only few-shot prompting techniques that contain varying numbers of “in-context examples” as shown in the figure above.
By evaluating GPT-3 on a range of language understanding tasks, we immediately see that using a larger model significantly benefits few-shot performance. On sentence completion tasks, for example, GPT-3 improves the current state-of-the-art (i.e., including approaches that use supervised training or fine-tuning!) on several popular datasets, and providing more in-context examples seems to further improve performance; see below.
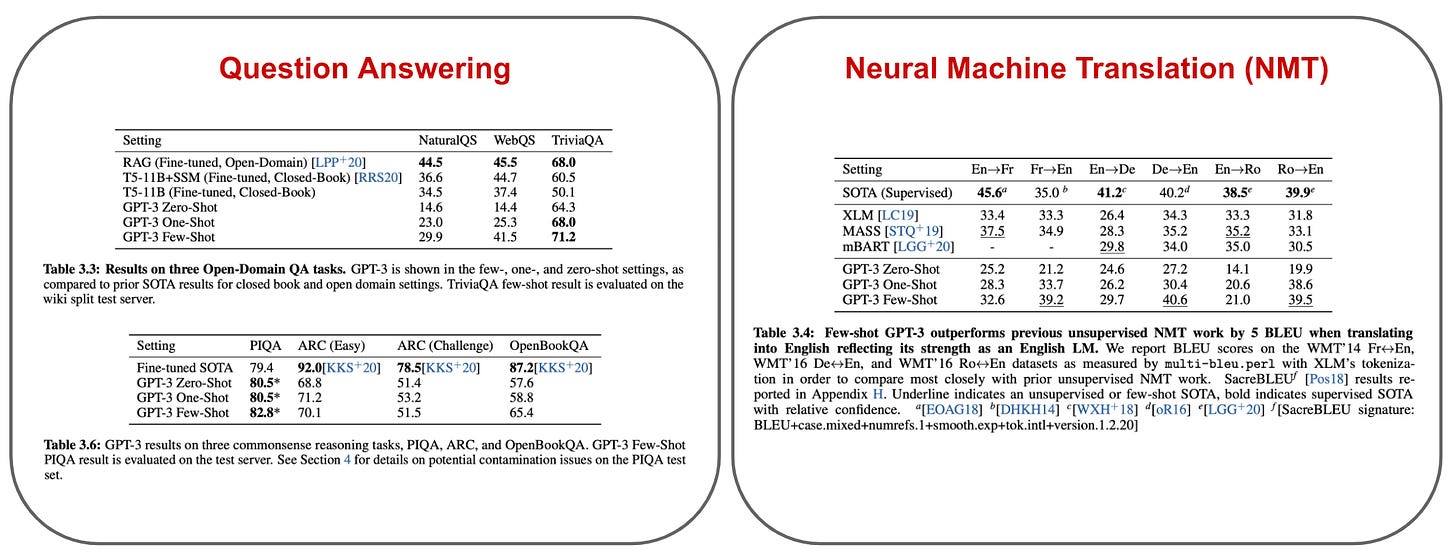
On question answering tasks, we see that GPT-3 is outperformed by models like T5 [7] or RoBERTa [8]. However, these models perform extensive, supervised fine-tuning, while GPT-3 achieves comparable results via task-agnostic, few-shot inference. Put simply, GPT-3’s performance on these tasks is still impressive because it is a completely generic LLM that has not been specialized to solving these tasks in any way.
When evaluating GPT-3 on translation tasks, we observe that GPT-3 is better than state-of-the-art unsupervised neural machine translation (NMT) techniques at translating from other languages into English. Such results are surprising given that GPT-3’s pre-training set contains only 7% non-English content and no explicit mixing of or translation between languages. Interestingly, GPT-3 is much less effective at translating from English into other languages; see below.
Authors also evaluate GPT-3 on the SuperGLUE benchmark, which contains a wide variety of different language understanding tasks. The results are summarized within the figure below, where we can see that (i) using more in-context examples benefits GPT-3’s performance and (ii) GPT-3 can even surpass the performance of popular, fine-tuned baselines like BERT [9].
Across all benchmarks, GPT-3 shows us that LLMs become more effective at task-agnostic, in-context learning as they grow in size. We can use in-context examples to prompt accurate responses from LLMs on a variety of tasks, making GPT-3 the first practical example of using general purpose LLMs to perform highly-accurate inference on a variety of downstream tasks without any task-specific modifications.
Despite the incredible leaps made by GPT-3 towards creating task-agnostic foundation models for language, these advancements come at a significant computational cost. GPT-3 was pre-trained on a special-purpose GPU cluster and its pre-training process required significantly more compute than any previous model that has been studied; see below.
Although recent work has drastically reduced the training cost of GPT-3 (i.e., from >$10M in compute costs to <$500K), such foundation models are still not cheap to obtain. If we want to create our own foundation model like GPT-3, we better make sure it performs well.
open-sourcing GPT-3. After the original proposal of GPT-3 in [2], the model was not publicly released. Rather, it was made accessible only via paid APIs. Although the model’s API was heavily used, this lack of open-source access to the model itself (and its training code) hindered further analysis and experimentation.
To eliminate this issue, an open-sourced version of GPT-3, called OPT-175B, was created and analyzed in [10]. The release of OPT-175B also included a full code repository and several logbooks that provided valuable insights into the LLM training process. To learn more about OPT-175B (and see code you can use to train LLMs like GPT-3!), check out the overview below.
Takeaways
GPT models were originally proposed and explored with the goal of creating generic language models that are capable of solving a wide variety of tasks. These models operate under the assumption that if we can understand language modeling (i.e., predicting the next word within a sequence) at a very granular level, then we can generalize this understanding in a lot of useful ways without the need for task-specific fine-tuning or adaptation.
Initially, LMs like GPT and GPT-2 fell short of this goal. Their task-agnostic performance was far worse than supervised baselines. Within this overview, however, we have learned that increasing the scale of these LMs is a viable path forward in creating high-performing, task-agnostic models for language understanding. Eventually, this line of thinking led to the proposal and analysis of GPT-3, a massive LLM (i.e., ~100X bigger than GPT-2) that far surpassed the task-agnostic performance of prior LMs.
scaling laws. Scaling up LMs (i.e., using larger models, more data, and more compute) can drastically improve their performance. As we increase the scale of LM training, we learn from findings in [1] that we should (i) significantly increase the size of the underlying model and (ii) increase the amount of data used for pre-training (and the batch size) to a lesser extent. Larger language models are more sample efficient, and their performance improves as a power law with respect to model size, data size, and the amount of training compute across several orders of magnitude. In other words, LMs get much better as we make them bigger.
how much can we scale? GPT-3 (an LLM with 175 billion parameters) empirically validates the trends outlined in [1] at an unprecedented scale. When we adopt this massive model and pre-train it over a large textual corpus, we see large improvements in task-agnostic, few-shot performance. GPT-3 is still outperformed by supervised techniques on several baselines, but findings in [2] provide clear evidence that LLMs improve in their ability to perform in-context learning as they grow in size. Though GPT-3 is technically similar to GPT-2, training a model of this scale is a feat of engineering that demonstrates the incredible potential of language foundation models.
New to the newsletter?
Hello! I am Cameron R. Wolfe, a research scientist at Alegion and PhD student at Rice University. I study the empirical and theoretical foundations of deep learning. This is the Deep (Learning) Focus newsletter, where I pick a single, bi-weekly topic in deep learning research, provide an understanding of relevant background information, then overview a handful of popular papers on the topic. If you like this newsletter, please subscribe, share it with your friends, or follow me on twitter!
Bibliography
[1] Kaplan, Jared, et al. "Scaling laws for neural language models." arXiv preprint arXiv:2001.08361 (2020).
[2] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.
[3] McCandlish, Sam, et al. "An empirical model of large-batch training." arXiv preprint arXiv:1812.06162 (2018).
[4] Radford, Alec, et al. "Improving language understanding by generative pre-training." (2018).
[5] Radford, Alec, et al. "Language Models are Unsupervised Multitask Learners."
[6] Child, Rewon, et al. "Generating long sequences with sparse transformers." arXiv preprint arXiv:1904.10509 (2019).
[7] Raffel, Colin, et al. "Exploring the limits of transfer learning with a unified text-to-text transformer." J. Mach. Learn. Res. 21.140 (2020): 1-67.
[8] Liu, Yinhan, et al. "Roberta: A robustly optimized bert pretraining approach." arXiv preprint arXiv:1907.11692 (2019).
[9] Devlin, Jacob, et al. "Bert: Pre-training of deep bidirectional transformers for language understanding." arXiv preprint arXiv:1810.04805 (2018).
[10] Zhang, Susan, et al. "Opt: Open pre-trained transformer language models." arXiv preprint arXiv:2205.01068 (2022).