This newsletter is supported by Alegion. At Alegion, I work on a range of problems from online learning to diffusion models. Feel free to check out our data annotation platform or contact me about potential collaboration/opportunities!
If you like this newsletter, please subscribe, share it, or follow me on twitter. Thank you for your support!
As we have seen with methods like DeepSDF [2] and SRNs [4], encoding 3D objects and scenes within the weights of a feed-forward neural network is a memory-efficient, implicit representation of 3D data that is both accurate and high-resolution. However, the approaches we have seen so far are not quite capable of capturing realistic and complex scenes with sufficient fidelity. Rather, discrete representations (e.g., triangle meshes or voxel grids) produce a more accurate representation, assuming a sufficient allocation of memory.
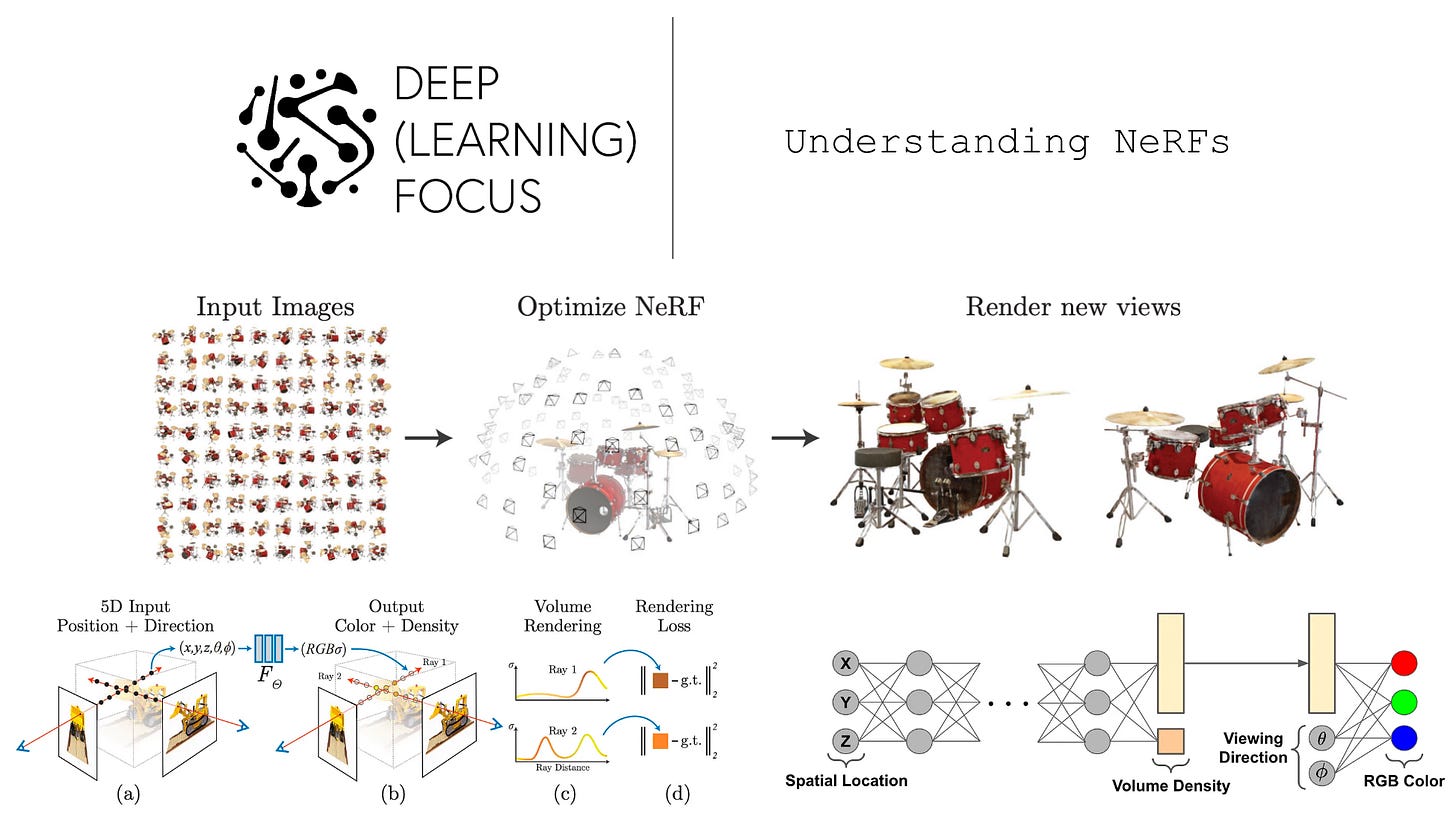
This changed with the proposal of Neural Radiance Fields (NeRFs) [1], which use a feed-forward neural network to model a continuous representation of scenes and objects. The representation used by NeRFs, called a radiance field, is a bit different from prior proposals. In particular, NeRFs map a five-dimensional coordinate (i.e., spatial location and viewing direction) to a volume density and view-dependent RGB color. By accumulating this density and appearance information across different viewpoints and locations, we can render photorealist, novel views of a scene.
Like SRNs [4], NeRFs can be trained using only a set of images (along with their associated camera poses) of an underlying scene. Compared with prior approaches, NeRF renderings are better both qualitatively and quantitatively. Notably, NeRFs can even capture complex effects such as view-dependent reflections on an object’s surface. By modeling scenes implicitly in the weights of a feed-forward neural network, we match the accuracy of discrete scene representations without prohibitive memory costs.
why is this paper important? This post is part of my series on deep learning for 3D shapes and scenes. NeRFs were a revolutionary proposal in this area, as they enable incredibly accurate 3D reconstructions of scene from arbitrary viewpoints. The quality of scene representations produced by NeRFs is incredible, as we will see throughout the remainder of this post.
Background
Most of the background concepts needed to understand NeRFs have been covered in prior posts on this topic, including:
Feed-forward neural networks [link]
Representing 3D objects [link]
Problems with discrete representations [link]
We only need to cover a few more background concepts before going over how NeRFs work.
Position Encodings
Instead of directly using [x, y, z] coordinates as input to a neural network, NeRFs convert each of these coordinates into higher-dimensional positional embeddings. We have discussed positional embeddings in previous posts on the transformer architecture, as positional embeddings are needed to provide a notion of token ordering and position to self-attention modules.
Put simply, positional embeddings take a scalar number as input (e.g., a coordinate value or an index representing position in a sequence) and produce a higher-dimensional vector as output. We can either learn these embeddings during training or use a fixed function to generate them. For NeRFs, we use the function shown above, which takes a scalar p as input and produces a 2L-dimensional position encoding as output.
Other Stuff
There are a few other (possibly) unfamiliar terms that we may encounter in this overview. Let’s quickly clarify them now.
end-to-end training. If we say that a neural architecture can be learned “end-to-end”, this just means that all components of a system are differentiable. As a result, when we compute the output for some data and apply our loss function, we can differentiate through the entire system (i.e., end-to-end) and train it with gradient descent!
Not all systems can be trained end-to-end. For example, if we are modeling tabular data, we might perform a feature extraction process (e.g., one-hot encoding), then train a machine learning model on top of these features. Because the feature extraction process is hand-crafted and not differentiable, we cannot train the system end-to-end!
Lambertian reflectance. This term was completely unfamiliar to me prior to reading about NeRFs. Lambertian reflectance refers to how reflective an object’s surface is. If an object has a matte surface that does not change when viewed from different angles, we say this object is Lambertian. Alternatively, a “shiny” object that reflects light differently based on the angle from which it is viewed would be called non-Lambertian.
Modeling NeRFs
The high-level process for rendering scene viewpoints with NeRFs proceeds as follows:
Generate samples of 3D points and viewing directions for a scene using a Ray Marching approach.
Provide the points and viewing directions as input to a feed-forward neural network to produce color and density output.
Perform volume rendering to accumulate colors and densities from the scene into a 2D image.
We will now explain each component of this process in more detail.
radiance fields. As mentioned before, NeRFs model a 5D vector-valued (i.e., meaning the function outputs multiple values) function called a radiance field. The input to this function is an [x, y, z] spatial location and a 2D viewing direction. The viewing direction has two dimensions, corresponding to the two angles that can be used to represent a direction in 3D space; see below.
In practice, the viewing direction is just represented as a 3D cartesian unit vector.
The output of this function has two components: volume density and color. The color is simply an RGB value. However, this value is view-dependent, meaning that the color output might change given a different viewing direction as input! Such a property allows NeRFs to capture reflections and other view-dependent appearance effects. In contrast, volume density is only dependent upon spatial location and captures opacity (i.e., how much light accumulates as it passes through that position).
the neural network. In [1], we model radiance fields with a feed-forward neural network, which takes a 5D input and is trained to produce the corresponding color and volume density as output; see above. Recall, however, that color is view-dependent and volume density is not. To account for this, we first pass the input 3D coordinate through several feed-forward layers, which produce both the volume density and a feature vector as output. This feature vector is then concatenated with the viewing direction and passed through an extra feed-forward layer to predict the view-dependent, RGB color; see below.
volume rendering (TL;DR). Volume rendering is too complex of a topic to cover here in-depth, but we should know the following:
It can produce an image of an underlying scene from samples of discrete data (e.g., color and density values).
It is differentiable.
For those interested in more details on volume rendering, check out the explanation below and Section 4 of [1].
the big picture. NeRFs use the feed-forward network to generate relevant information about a scene’s geometry and appearance along numerous different camera rays (i.e., a line in 3D space moving from a specific camera viewpoint out into a scene along a certain direction), then use rendering to aggregate this information into a 2D image.
Notably, both of these component are differentiable, which means we can train this entire system end-to-end! Given a set of images with corresponding camera poses, we can train a NeRF to generate novel scene viewpoints by just generating/rendering known viewpoints and using (stochastic) gradient descent to minimize the error between the NeRF’s output and the actual image; see below.
a few extra details. We now understand most of the components of a NeRF. However, the approach that we’ve described up to this point is actually shown in [1] to be inefficient and generally bad at representing scenes. To improve the model, we can:
Replace spatial coordinates (for both the spatial location and the viewing direction) with positional embeddings.
Adopt a hierarchical sampling approach for volume rendering.
By using positional embeddings, we map the feed-forward network’s inputs (i.e., the spatial location and viewing direction coordinates) to a higher-dimension. Prior work showed that such an approach, as opposed to using spatial or directional coordinates as input directly, allows neural networks to better model high-frequency (i.e., changing a lot/quickly) features of a scene [5]. This makes the quality of the NeRF’s output much better; see below.
The hierarchical sampling approach used by NeRF makes the rendering process more efficient by only sampling (and passing through the feed-forward neural network) locations and viewing directions that are likely to impact the final rendering result. This way, we only evaluate the neural network where needed and avoid wasting computation on empty or occluded areas.
Show us some results!
NeRFs are trained to represent only a single scene at once and are evaluated across several datasets with synthetic and real objects.
As shown in the table above, NeRFs outperform alternatives like SRNs [4] and LLFF [6] by a significant, quantitative margin. Beyond quantitative results, it’s really informative to look visually at the outputs of a NeRF compared to alternatives. First, we can immediately tell that using positional encodings and modeling colors in a view-dependent manner is really important; see below.
One improvement that we will immediately notice is that NeRFs—because they model colors in a view-dependent fashion—can capture complex reflections (i.e., non-Lambertian features) and view-dependent patterns in a scene. Plus, NeRFs are capable of modeling intricate aspects of underlying geometries with surprising precision; see below.
The quality of NeRF scene representations is most evident when they are viewed as a video. As can be seen in the video below, NeRFs model the underlying scene with impressive accuracy and consistency between different viewpoints.
For more examples of the photorealistic scene viewpoints that can be generated with NeRF, I highly recommend checking out the project website linked below!
Takeaways
As we can see in the evaluation, NeRFs were a massive breakthrough in scene representation quality. As a result, the technique gained a lot of popularity within the artificial intelligence and computer vision research communities. The potential applications of NeRF (e.g., virtual reality, robotics, etc.) are nearly endless due to the quality of its scene representations. The main takeaways are listed below.
NeRFs capture complex details. With NeRFs, we are able to capture fine-grained details within a scene, such as the rigging material within a ship; see above. Beyond geometric details, NeRFs can also handle non-Lambertian effects (i.e., reflections and changes in color based on viewpoint) due to their modeling of color in a view-dependent manner.
we need smart sampling. All approaches to modeling 3D scenes that we have seen so far use neural networks to model a function on 3D space. These neural networks are typically evaluated at every spatial location and orientation within the volume of space being considered, which can be quite expensive if not handled properly. For NeRFs, we use a hierarchical sampling approach that only evaluates regions that are likely to impact the final, rendered image, which drastically improves sample efficiency. Similar approaches are adopted by prior work; e.g., ONets [3] use an octree-based hierarchical sampling approach to extract object representations more efficiently.
positional embeddings are great. So far, most of the scene representation methods we have seen pass coordinate values directly as input to feed-forward neural networks. With NeRFs, we see that positionally embedding these coordinates is much better. In particular, mapping coordinates to a higher dimension seems to allow the neural network to capture high-frequency variations in scene geometry and appearance, which makes the resulting scene renderings much more accurate and consistent across views.
still saving memory. NeRFs implicitly model a continuous representation of the underlying scene. This representation can be evaluated at arbitrary precision and has a fixed memory cost—we just need to store the parameters of the neural network! As a result, NeRFs yield accurate, high-resolution scene representations without using a ton of memory.
“Crucially, our method overcomes the prohibitive storage costs of discretized voxel grids when modeling complex scenes at high-resolutions.” - from [1]
limitations. Despite significantly advancing state-of-the-art, NeRFs are not perfect—there is room for improvement in representation quality. However, the main limitation of NeRFs is that they only model a single scene at a time and are expensive to train (i.e., 2 days on a single GPU for each scene). It will be interesting to see how future advances in this area can find more efficient methods of generating NeRF-quality scene representations.
New to the newsletter?
Hello! I am Cameron R. Wolfe, a research scientist at Alegion and PhD student at Rice University. I study the empirical and theoretical foundations of deep learning.
This is the Deep (Learning) Focus newsletter, where I help readers to build a deeper understanding of topics in deep learning research via understandable overviews of popular papers on that topic. If you like this newsletter, please subscribe, share it with your friends, or follow me on twitter!
Bibliography
[1] Mildenhall, Ben, et al. "Nerf: Representing scenes as neural radiance fields for view synthesis." Communications of the ACM 65.1 (2021): 99-106.
[2] Park, Jeong Joon, et al. "Deepsdf: Learning continuous signed distance functions for shape representation." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.
[3] Mescheder, Lars, et al. "Occupancy networks: Learning 3d reconstruction in function space." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.
[4] Sitzmann, Vincent, Michael Zollhöfer, and Gordon Wetzstein. "Scene representation networks: Continuous 3d-structure-aware neural scene representations." Advances in Neural Information Processing Systems 32 (2019).
[5] Rahaman, Nasim, et al. "On the spectral bias of neural networks." International Conference on Machine Learning. PMLR, 2019.
[6] Mildenhall, Ben, et al. "Local light field fusion: Practical view synthesis with prescriptive sampling guidelines." ACM Transactions on Graphics (TOG) 38.4 (2019): 1-14.