This newsletter is supported by Alegion. At Alegion, I work on a range of problems from online learning to diffusion models. Feel free to check out our data annotation platform or contact me about potential collaboration/opportunities!
If you like this newsletter, please subscribe, share it, or follow me on twitter. Thank you for your support!
The problem of 3D reconstruction aims to produce a high-resolution object representation given a noisy view of the object (e.g., partial point cloud, 2D image, etc.) as input. Recently, deep neural networks have become a popular approach for 3D reconstruction, as they can encode prior information that helps to handle ambiguity. Put simply, this means that if the correct way to reconstruct a given object is unclear from the input, a neural network can draw from its experience with other data points that it has seen during training to still produce a reasonable output.
Most 3D reconstruction approaches were originally limited in their ability to represent high-resolution objects. Voxels, point clouds, and meshes all fell short of modeling high-resolution objects in a memory efficient manner. Compared to models like GANs [2] that could generate high-resolution, realistic images, comparable approaches for generating 3D geometries were primitive.
To solve this problem, authors in [1] develop a 3D reconstruction approach that models occupancy functions with neural networks. More specifically, we train a neural network to predict whether a given point in space is occupied (or not) by an object (i.e., an occupancy function!). Then, the underlying object is represented by the decision boundary (i.e., locations where predictions switch from occupied to not occupied) of this neural network; see above. Occupancy networks (ONets) can represent and reconstruct 3D shapes with arbitrary precision and reasonable memory requirements.
why is this paper important? This post is part of my series on deep learning for 3D shapes and scenes. This area was recently revolutionized by the proposal of NeRF [2], which enables accurate 3D reconstructions of scenes from a few photos of different viewpoints; see above. With a NeRF representation, we can produce an arbitrary number of synthetic viewpoints of this scene or even generate 3D representations of relevant objects; see below.
ONets are a background methodology that is referenced by NeRF. Currently, we are surveying prior work that is relevant to understanding more modern methods. After understanding the workings and limitations of these approaches, we will build up to an understanding of NeRF (and methods that follow it)!
Background
In our prior review of DeepSDF for 3D shape generation, we covered a few relevant background concepts, including:
Most neural networks in [1] use a simple, feed-forward architecture, which serves as an alternative to storing 3D shapes in their canonical mesh, voxel, or point cloud formats. To understand why this is preferable, we have to go into a bit more detail regarding the limitations of these representations.
Shortcomings of 3D Shape Representations
3D geometries are typically stored or represented as meshes, voxels, or point clouds; see above. Given that these representations are available, why would we want to represent shapes using a neural network instead? The simple answer is that (i) other representations have some notable limitations and (ii) we can save a lot of memory this way.
voxels are memory inefficient. In deep learning applications, voxels are the most widely-used representations for 3D shapes due to their simplicity—they are a straightforward generalization of pixels to 3D space. If we encode a 3D shape using voxels, however, the memory footprint of this encoding grows cubically with its resolution. If we want a more precise voxel representation, we will need to use a lot more memory.
point clouds are disconnected. Point clouds are similar in format to data that we would typically get from sensors like LiDAR, but the resulting geometry is disconnected—it is just a bunch of points in 3D space. As a result, extracting the actual 3D shape from this data requires expensive post-processing procedures.
meshes aren’t the solution. If point clouds need post-processing and voxels aren’t memory efficient, we should use meshes, right? Unfortunately, most mesh representations are actually based upon deforming a “template” mesh. In practice, this means that meshes cannot encode arbitrary topologies, meaning that they are limited in their ability to accurately represent certain geometries.
what should we do then? With these limitations in mind, the approach proposed in [1] starts to make a little more sense. Instead of directly storing mesh, voxel, or point cloud representations of 3D shapes, we can train a neural network to generate output from which the shape can be recovered. This way, we can store a bunch of different geometries within the parameters of a single neural network, which has a fixed memory cost!
Occupancy Functions
The work in [1] represents occupancy functions with neural networks, but what is an occupancy function? Put simply, this is just a function that takes a point in space as an input (e.g., an [x, y, z] coordinate) and returns a binary output, representing whether this location is “occupied” by the object in question.
Such functions can be approximated with a neural network that is taught to output a probability between zero and one given an [x, y, z] coordinate as input.
extracting an isosurface. To extract a 3D geometry from an occupancy function, we have to find an isosurface. To do this, we just find points in 3D space at which the occupancy function is equal to some threshold, which we will call t.
Here, t is set to some value between zero and one. Thus, the isosurface represents the boundary of the occupancy function, where the output switches from zero to one (or vice versa)—this just corresponds to the surface of the underlying object!
Evaluation Metrics
The metrics used to judge the quality of 3D shapes is quite similar to the metrics that we see in normal computer vision. The main metrics used in [1] are explained below.
volumetric IoU. The volume of two shapes’ intersection divided by the volume of their union. This metric is the same as normal IoU, but it has been generalized to work in three dimensions.
chamfer-L1. The mean of accuracy and completeness. Accuracy is the mean distance of points on an output mesh to the nearest point on the ground truth mesh. Completeness is the same, but in the opposite direction.
normal consistency. We take a face normal (i.e., a vector that’s orthogonal to the plane of one of the mesh’s faces) of the predicted mesh, find the face normal of the corresponding nearest neighbor in the other mesh, then take the absolute value of these vectors’ dot product. By repeating this process over all normals in the predicted mesh and taking a mean, we get the normal consistency. This one’s a bit tougher to understand, but it’s useful for determining whether higher-order information is captured in the predicted shape (i.e., whether the faces of the two meshes tend to point in the same direction).
Occupancy Networks [1]
Given our prior overview of DeepSDF, the first question we might ask about Occupancy Networks is: Why model an occupancy function instead of alternatives like signed distance functions (SDFs)? The basic answer is that occupancy functions are much easier to learn.
“[SDFs are] usually much harder to learn compared to occupancy representations as the network must reason about distance functions in 3D space instead of merely classifying a voxel as occupied or not.” - from [1]
the network. To approximate an occupancy function, we use a feed-forward neural network that assigns a probability between zero and one to any 3D coordinate. The network’s input includes:
A (single) 3D coordinate.
Noisy observations of the underlying object.
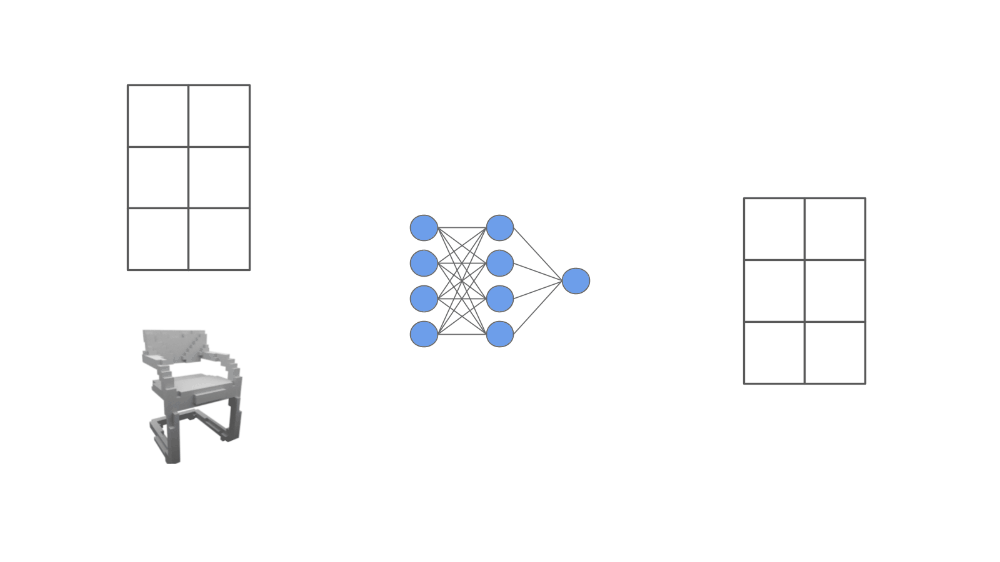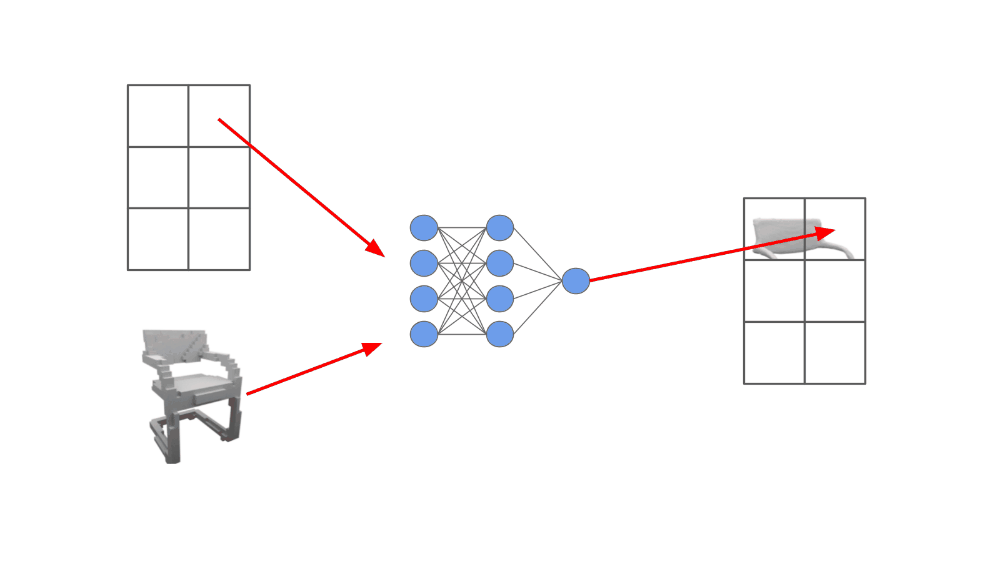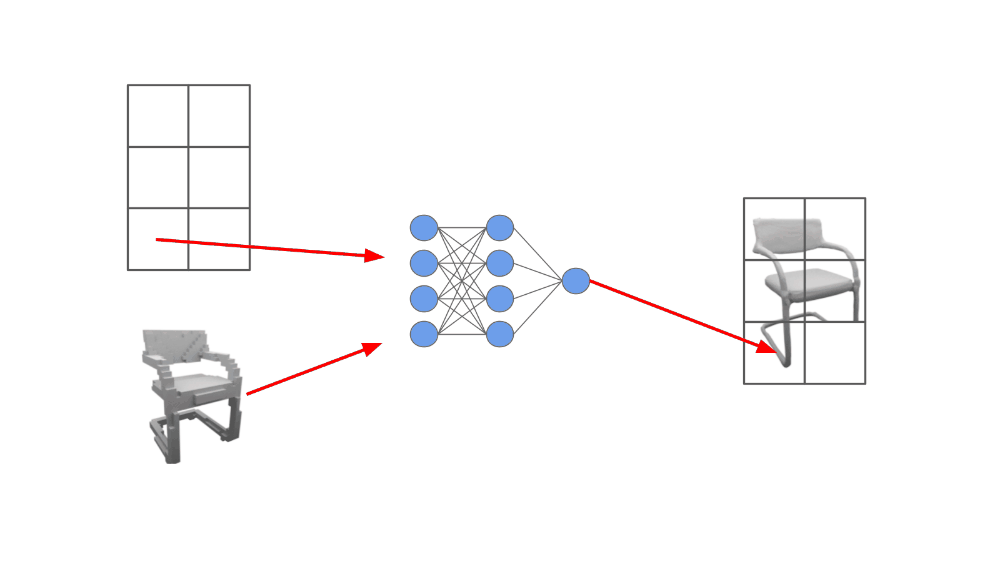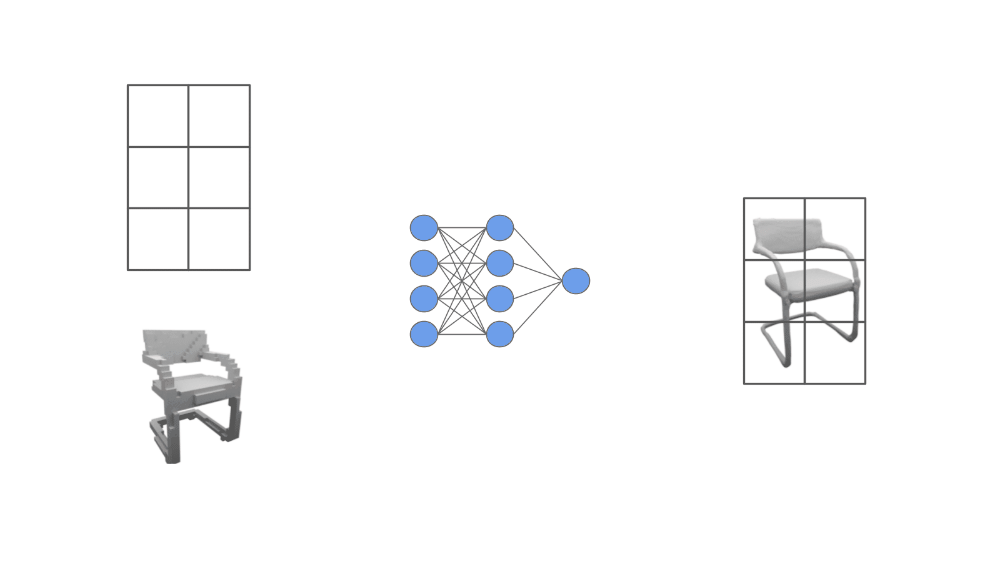
The network, which we call an ONet, outputs a scalar probability. The noisy observations of the underling object that are passed as input to the model could be something like an incomplete point cloud or a coarse voxel grid. We are conditioning the neural network on this noisy data, then using it to produce a much more accurate representation of the object; see below.
We cannot directly pass the observed, noisy object data as input to the feed-forward neural network because it many come in many different formats. Instead, authors in [1] embed this data (i.e., turn it into a vector) using different neural network-based encoders (e.g., ResNets [4] for images or PointNet [5] for point clouds; these are just common network architectures for converting images and point clouds to vectors).
Then, the first layer of the feed-forward neural network uses conditional batch normalization—a class-conditional batch normalization variant—to adapt the network’s input based upon the object embedding. In this way, we ensure that the ONet’s input is conditioned upon the data that is already available about the 3D geometry we are trying to reconstruct.
training. To train the ONet, we (i) consider a padded volume of space around an object used for training and (ii) uniformly sample K occupancy function values throughout this space. A mini-batch is formed by applying this sampling procedure to several training objects. We train the network normally using mini-batch gradient descent with a cross entropy loss that is applied per occupancy function value in the mini-batch.
generating objects. Once the ONet is trained, we can output occupancy function values given a spatial location at arbitrary resolution. But, how do we use this to create an actual 3D object (e.g., in mesh format)? To do this, authors in [1] propose a Multi-resolution IsoSurface Extraction (MISE) procedure.

This procedure is inspired by the idea of an octree, a tree data structure that recursively represents 3D space. Each octree node has eight children, and we can recursively add children to each node to represent a volume with higher resolution. A 2D visualization of this process is provided above.
The basic procedure for MISE is as follows:
Discretize space at an initial resolution
Evaluate the ONet at each discrete location in this space
Mark all voxels that have at least two adjacent voxels with differing occupancy
Divide marked voxels into eight sub-voxels and repeat until the desired resolution is reached
Apply Marching Cubes to obtain a mesh
Thus, MISE obtains a mesh by recursively evaluating the ONet at higher resolutions where it is needed (i.e., close to the object boundary). Although we must apply a few extra steps to refine this mesh, the overall process is pretty intuitive; see below.
experimental results. ONets are mostly evaluated on the synthetic ShapeNet dataset based on their ability to represent complex 3D shapes and/or reconstruct them from images, noisy point clouds, and low resolution voxel grids. In these experiments, we see that ONets can accurately represent the “Chair” portion of ShapeNet. Using an ON, we can encode nearly 5K objects independently of resolution using only 6M parameters. In contrast, voxel representations are not as accurate and their memory requirements increase with the desired resolution; see below.
In reconstruction experiments, we continue to see that ONets work quite well. They can recover complicated shapes and tend to produce results that are closest to the ground truth geometry. Most baseline methodologies tend to suffer from limitations, such as producing coarse representations, disconnected objects that require post-processing, or objects that lack relevant details. Qualitative examples of model output are shown below.
When trying to reconstruct geometries from noisy point clouds and coarse voxel grids (i.e., instead of images as is done above), we see that the ONet continues to perform quite well; see below.
other stuff. ONets are also applied to real-world data by taking images from KITTI and the Online Products datasets. Despite being trained on only synthetic data, the ONet seems to generalize pretty well to this type of data. Notably, however, the authors do use segmentation masks provided by KITTI to extract pixels associated with the desired object. Some examples of the reconstructions generated from these datasets are shown below.
Beyond the initial proposal in [1], the authors also propose a generative version of the ONet that is trained in an unsupervised fashion over ShapeNet and forms a latent space of 3D geometries using approach that is similar to a Variational Auto-Encoder (VAE).
Put simply, the authors find that you can create generative ONets that can create new meshes and interpolate between meshes. This is useful if we want to focus on generative applications instead of 3D reconstruction in particular.
Takeaways
Prior to ONets, existing methods for 3D reconstruction struggled to model high-resolution objects while maintaining a reasonable memory footprint. In [1], we learn that a smarter representation of 3D geometries can provide a significant benefit. The major takeaways from the proposal of ONets are outlined below.
occupancy functions are great. Common representations of 3D geometries (e.g., meshes, point clouds, voxels) tend to use too much memory when representing high-resolution objects. Occupancy functions are a more concise representation that allow us to model 3D objects with arbitrary precision by encoding a single function. Plus, occupancy functions are easier to learn or model compared to alternatives like SDFs.
learnable reconstruction. Sure, occupancy functions are great, but the real value in this work is how we represent these functions. Namely, we can use neural networks to learn and store occupancy functions for a variety of shapes. As a result, we can represent many different shapes at arbitrary precision just by (i) training an ONet and (ii) storing the model’s parameters. This approach uses a limited, fixed amount of memory and improves reconstruction quality by leveraging prior information!
representing 3D space. Here, we quickly encountered the concept of an octree when explaining the MISE approach for generating meshes with ONets. This is an important data structure for 3D modeling that allows us to recursively generate shapes with varying levels of precision. If we want to get a more precise representation, we just continue subdividing voxels. But, we should only do this where it makes sense (i.e., when nearby voxels have differing occupancy) to avoid unnecessary computation.
New to the newsletter?
Hello! I am Cameron R. Wolfe, a research scientist at Alegion and PhD student at Rice University. I study the empirical and theoretical foundations of deep learning.
This is the Deep (Learning) Focus newsletter, where I help readers to build a deeper understanding of topics in deep learning research via series of short, focused overviews of popular papers on that topic. Each overview contains explanations of all relevant background information or context. A new topic is chosen (roughly) every month, and I overview two papers each week (on Monday and Thursday). If you like this newsletter, please subscribe, share it with your friends, or follow me on twitter!
Bibliography
[1] Mescheder, Lars, et al. "Occupancy networks: Learning 3d reconstruction in function space." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.
[2] Goodfellow, Ian, et al. "Generative adversarial networks." Communications of the ACM 63.11 (2020): 139-144.
[3] Mildenhall, Ben, et al. "Nerf: Representing scenes as neural radiance fields for view synthesis." Communications of the ACM 65.1 (2021): 99-106.
[4] He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
[5] Qi, Charles R., et al. "Pointnet: Deep learning on point sets for 3d classification and segmentation." Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.
[6] Hoang, Long, et al. "A deep learning method for 3D object classification using the wave kernel signature and a center point of the 3D-triangle mesh." Electronics 8.10 (2019): 1196.