Graph-Based Prompting and Reasoning with Language Models
Understanding graph of thoughts prompting and several variants...
This newsletter is presented by Deci AI. Deci does a ton of interesting AI research. Most recently, they released DeciCoder-1B, an open-source code generation model. Read about it here or download it on HuggingFace.
If you like the newsletter, feel free to get in touch with me or follow me on Medium, X, and LinkedIn. I try my best to produce useful/informative content.
Advanced prompting techniques like chain of thought [8] and tree of thought [9] prompting have drastically improved the ability of large language models (LLMs) to solve complex, reasoning-based tasks. At a high level, forcing the LLM to construct a step-by-step response to a problem drastically improves its problem-solving capabilities. However, all of such techniques assume that the reasoning process should follow a linear patterns that progresses from one thought to the next. Notably, the reasoning process followed by humans tends to be quite different, following multiple different chains of thought and even combining insights from different thoughts to arrive at a final solution. Within this overview, we will studying several prompting techniques that model the reasoning process as a graph structure—rather than a chain or tree—that better captures the various types of non-linear patterns that may occur when reasoning over a problem.
“Human thinking is often characterized by its ability to make sudden leaps and connections between seemingly unrelated ideas, which can lead to novel insights and solutions. This non-linear, jumping thought process is a hallmark of human creativity, reasoning, and problem-solving abilities.” - from [1]
Background Information
Within this overview, we will explore several advanced prompting techniques for LLMs that can be used to solve difficult multi-step reasoning problems. Luckily, we have recently overviewed the basic ideas behind prompting, including:
Prompting basics (i.e., prompt engineering, context windows, structure of a prompt, etc.) [link]
Simple prompting techniques (e.g., zero/few-shot learning and instruction prompting) [link]
Advanced prompting techniques (e.g., chain of thought, self-consistency, and least-to-most prompting) [link]
We have covered both practical and advanced prompting techniques in the past. All of these concepts—especially chain of thought (CoT) prompting [8], self-consistency [10], and tree of thought (ToT) prompting [9]—will be relevant for gaining an understanding of this overview. Beyond these ideas, we need to understand the transformer architecture and the graph convolutional network (GCN) [13], which is applicable to machine learning on graph-structured data.
The Transformer from Top to Bottom
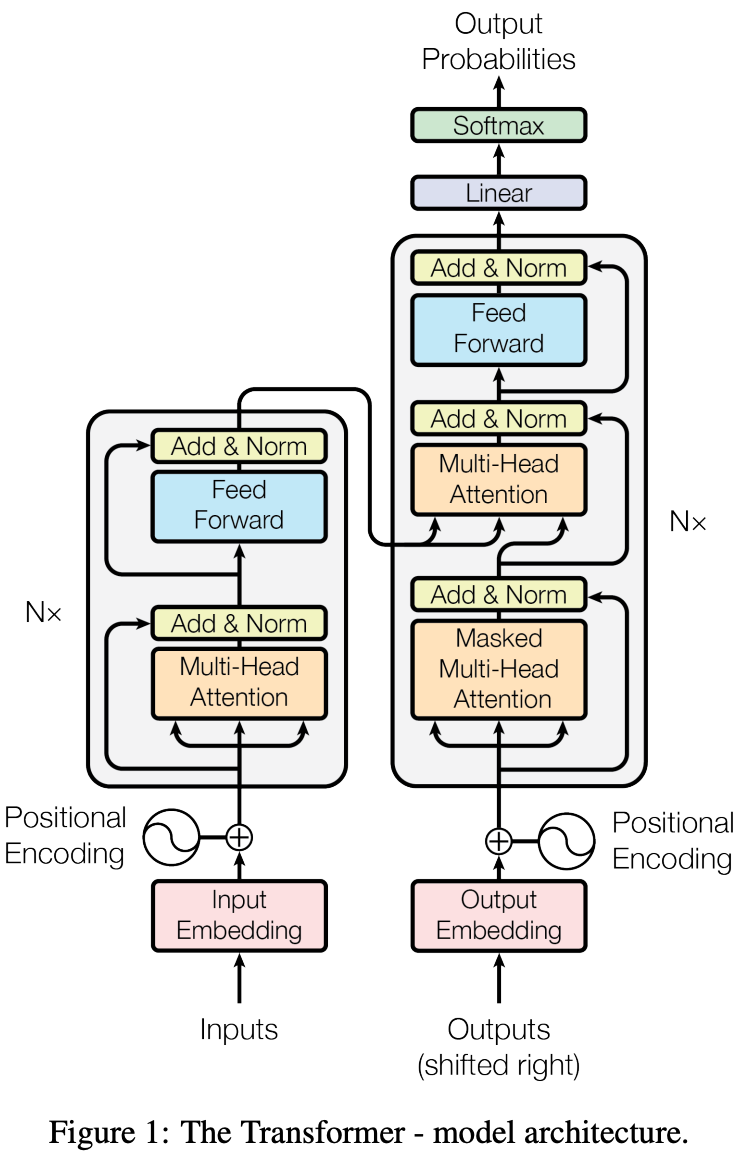
The transformer architecture, proposed in [11], was originally applied to Seq2Seq1 tasks (e.g., language translation). However, this model—and several of its variants—has since evolved to capture a variety of different use cases, such as:
Vision transformers [4] for object detection and classification in images
Many deep learning architectures are used in practice, but the transformer is unique in its scope—it is a single architecture that can be applied to a massive variety of tasks. First, we will learn about the standard, encoder-decoder transformer architecture, then we will extend this discussion to other notable variants.
Encoder-decoder transformers. The transformer has two components:
Encoder: each block contains bidirectional, multi-headed self-attention and a feed-forward transformation (usually a two-layer feed-forward network).
Decoder: each block contains masked self-attention, cross-attention, and a feed-forward transformation.
In prior overviews, we have discussed how raw text is processed before being ingested by a transformer. This processing converts text into a sequence of vectors—with added positional information—corresponding to each token in the input. This sequence of vectors is then ingested by the transformer’s encoder, which performs the operations described above. See below for a depiction.
The output of this block is simply a sequence of token vectors that have been transformed via bidirectional self-attention and a feed-forward neural network. We can then take the resulting sequence that has been passed though all blocks of the encoder and use it as input for the decoder component. Put simply, the encoder forms a representation of the entire input sequence using bidirectional self-attention, meaning that every token within the input sequence considers all other tokens in the sequence when crafting the encoder’s output sequence.
The decoder then ingests the encoder’s output and uses this representation of the input sequence as context when generating output. The decoder portion of the transformer is similar to the encoder with two main differences:
It uses masked self-attention.
It has an added cross-attention mechanism.
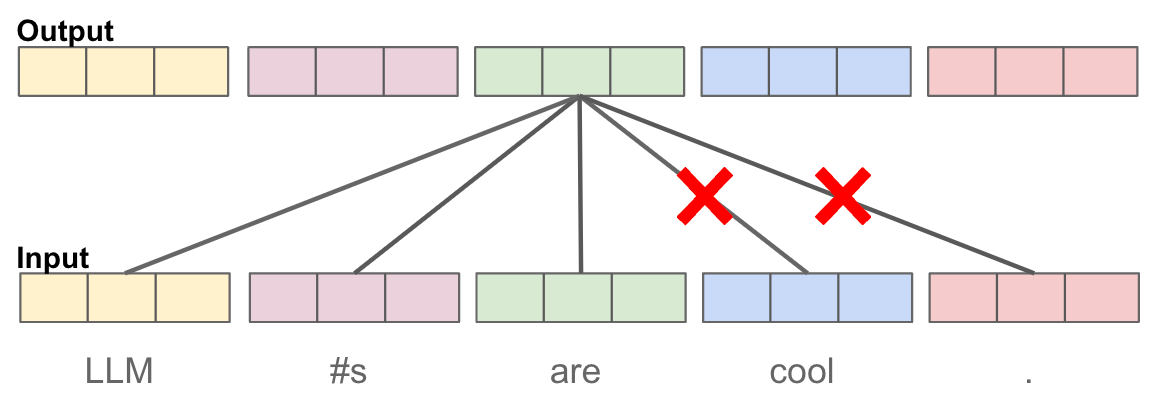
Masked self-attention restricts the multi-headed self-attention operation in the decoder from “looking forward” in the sequence. In other words, each token’s representation only depends on the tokens that come before it; see below.
Such a modification is necessary because the decoder is expected to generate a textual sequence as output. If the decoder used bidirectional self-attention, the model would be able to “cheat” during training by looking at the correct next token within the target sequence and copying it when predicting the next token. Masked self-attention avoids this issue and can be efficiently trained to generate coherent text via next token prediction. Cross attention is similar to any other attention operation, but it fuses two separate sequences—from the encoder and the decoder—with a single attention operation. See here for more details.
Example of the encoder-decoder architecture. One notable and widely-used example of a standard, encoder-decoder transformer architecture is the text-to-text transformer (T5) model [5]. This model is heavily used for transfer learning tasks with natural language and is even used by one of the prompting techniques that we will learn about in this overview. Analysis of T5 shows us that encoder-decoder transformers are useful for Seq2Seq tasks and prefix language modeling tasks2, which are both common practical problems. To learn more about the T5 architecture, feel free to check out the prior overview on this topic linked below.
Encoder-only and decoder-only variants. Within the explanation of T5 linked above, we learn extensively about the different variants of the transformer architecture. The two most notable variants are encoder-only and decoder-only models, both of which are relatively self-explanatory. Encoder-only architectures use the encoder portion of the transformer and completely eliminate the decoder. Such an architecture was popularized by BERT [12] and is incredibly effective when fine-tuned on a variety of different discriminative language tasks (e.g., sentence classification, named entity recognition, question answering, etc.).
Similarly, decoder-only architectures just eliminate the encoder portion of the transformer. However, this means that we also must get rid of any cross-attention modules due to the lack of an encoder; see above. As such, each block of a decoder-only transformer just performs masked self-attention and a feed-forward transformation. These architectures have exploded in popularity recently due to their heavy use in large, causal language models. Most of the generative LLMs that are widely studied today—GPT variants, PaLM, Falcon, LLaMA-2, etc.—rely upon a decoder-only transformer architecture.
AI with Graph-Structured Data
Within this overview, we will learn about prompting techniques that leverage a graph data structure to model the reasoning processes. With this in mind, we need to learn about how graph-structured data is usually handled within machine learning applications. Namely, most model architectures (e.g., transformers or convolutional neural networks) are meant for handling Euclidean data (e.g., images or text) that can easily be represented as a matrix. However, not all data is Euclidean. In fact, many sources of real world data are more appropriately modeled as a graph (e.g., social networks, molecules, etc.). For such data, we use a special model architecture called a graph convolutional network (GCN) [13].
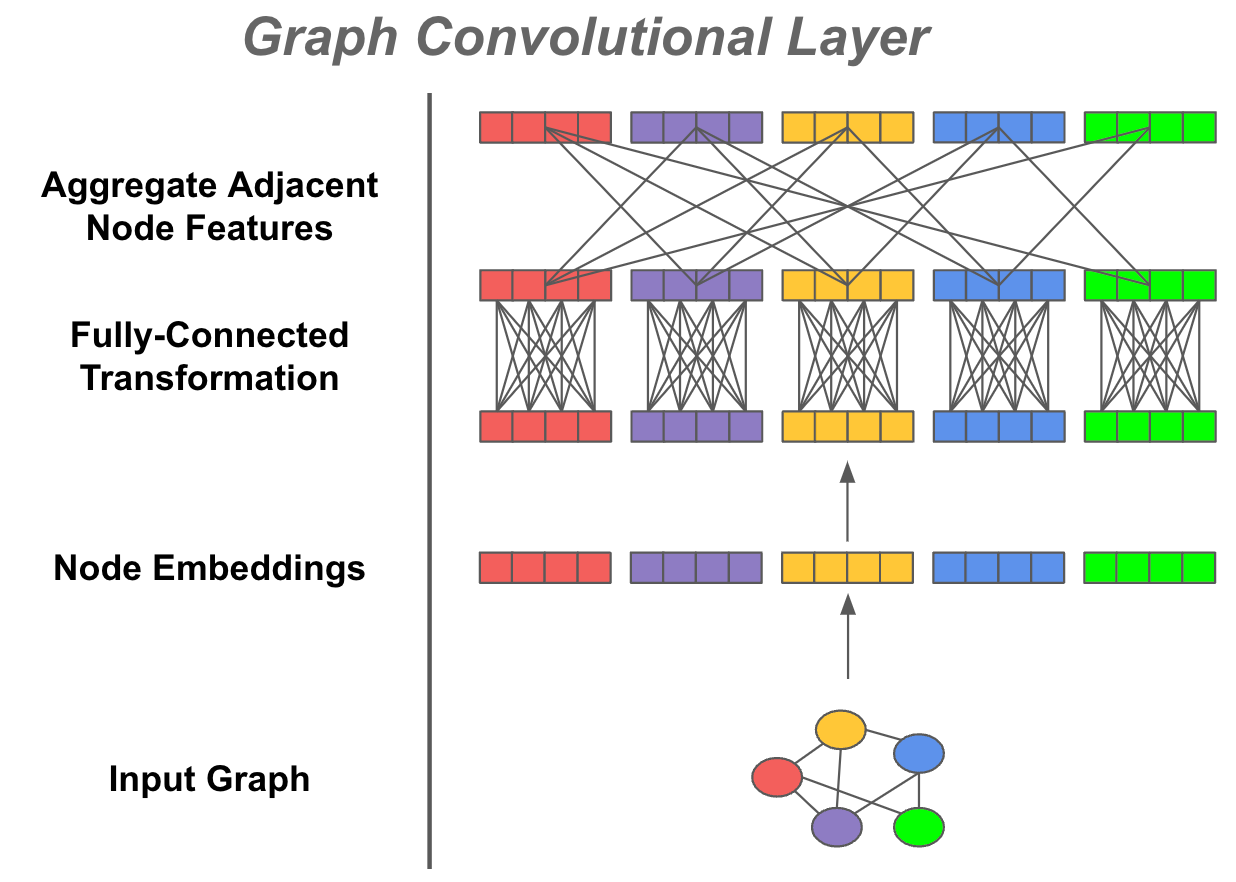
Understanding the GCN. At their core, GCNs are not much different from your typical feed-forward neural network. Given a graph, we associate each node in this graph with an input embedding, which can come from a variety of sources (e.g., embedding of a document, features corresponding to a user, etc.). Then, in each layer of the GCN, we first apply a feed-forward transformation to each node embedding (and normalization). Then, we incorporate the structure of the underlying graph by aggregating neighboring features for each node, such as by taking an average of all neighboring node embeddings; see above. By adding multiple layers to the GCN, we can learn rich node representations that capture both the properties of each node and the structure of the graph; read more below.
Other architectures. The GCN architecture has gained a massive amount of popularity and is widely-used in a variety of impressive, large-scale applications (e.g., Google Maps). Given this popularity, several extensions to the GCN have been proposed, including new architectural variants.. One notable example, which we will see used in this overview, is the Graph Attention Network (GAT).
The GAT [14] architecture is somewhat similar to the GCN, but it doesn’t just perform a simple average to aggregate features from neighboring nodes. Rather, a weighted average is taken over neighboring node features, where the weights are computed using an attention mechanism. The attention mechanism used in [14] is simple—it just takes two concatenated node embeddings as input and performs a feed-forward transformation to compute a score; see above. Such an approach allows more general aggregations of neighboring features to be learned.
Multi-Modal CoT Reasoning
Finally, before moving on to graph-based prompting techniques, there is one final prompting technique of which we will want to be aware—multi-modal chain of thought prompting [3]. This method, depicted above, proposes a two-stage approach for solving reasoning problems with both textual and visual inputs. In the first stage, the model takes both text and images as inputs and uses them to generate a problem-solving rationale similar to a chain of thought [8]. Then, this rationale is concatenated with the input and passed though the model—along with the images—once again to produce a final answer. Notably, this approach uses a T5 architecture [5] and is fine-tuned on the tasks that it solves. As we will see, the approach used by graph of thought reasoning [1] is quite similar.
Going Beyond Chain (or Tree) of Thought
Although CoT prompting is incredibly impactful, we have seen that it has important limitations. Most notably, it generates problem solving rationales in a left-to-right fashion using next token prediction, which prevents the model from recovering from early mistakes in the reasoning process. One solution to this problem is Tree of Thoughts (ToT) prompting (shown above), which enables backtracking and strategic lookahead over intermediate reasoning steps modeled as a tree. Despite its utility, ToT prompting still models reasoning and problem solving as a linear process that progresses over a single path of nodes within a tree, which fundamentally limits the capabilities of this prompting technique.
“By representing thought units as nodes and connections between them as edges, our approach captures the non-sequential nature of human thinking and allows for a more realistic modeling of thought processes.” - from [1]
As we have discussed, humans do not reason linearly. Rather, we make leaps and connections between ideas that lead to novel insights. Inspired by this idea, researchers have recently extended chain and tree of thoughts prompting to graph-structured data. In other words, we model the reasoning process as a graph, rather than as a chain or tree. In this section, we will overview this work and how it can be used to improve the reasoning capabilities of LLMs.
Beyond Chain-of-Thought, Effective Graph-of-Thought Reasoning in Large Language Models [1]
In [1], authors propose a two-stage reasoning framework3, called graph-of-thought reasoning (we’ll call it GOTR for short), for solving reasoning tasks with textual (and potentially visual) inputs. In the first stage, the language model is used to generate a problem-solving rationale. Then, the second stage uses this generated rationale to arrive at a final answer. This two-stage process is inspired by multi-modal CoT [3]. The GOTR framework relies upon three different kinds of inputs during the reasoning process:
Text: This is just the normal, textual input that we get for any prompt-based reasoning task.
Image: We can (optionally) ingest an image that is associated with the reasoning task.
Thought Graph: We generate a graph of all named entities within the textual input and their relationships to use as input.
As we will see, each of these inputs are given separate encoders within [1]. Then, the representations generated by each of these encoders is fused and passed to a decoder module that can generate output—either a rationale or final answer.
“By representing thought units as nodes and connections between thoughts as edges, the Graph-of-Thought captures the rich, non-sequential nature of human thinking and allows for a more realistic and logical modeling of reasoning processes.” - from [1]
Two-stage framework. As mentioned above, GOTR operates in a two-stage framework. In the first stage, the model is given the input text for the problem being solved and is expected to generate a problem-solving rationale—similar to a chain of thought. Then, the rationale that is generated during the first phase is just concatenated with the input text, and we generate output once again. The only difference between the first and second stages is that:
The second stage has a longer input (i.e., both input text and the rationale).
The second stage generates a final answer rather than a rationale.
However, the structure of both stages is identical other than the modified inputs and outputs. This two-stage process followed by GOTR is depicted below, where we see that two different kinds of outputs are generated in each stage.
Generating the thought graph. As mentioned before, GOTR takes three sources of data as input: text, images, and a thought graph. The image data is completely optional—GOTR works perfectly fine without it. But, we might be wondering: Where does the thought graph come from? Interestingly, we see in [1] that the thought graph is constructed based on the input text. A depiction of this is shown below.
More specifically, the thought graph in GOTR is used to represent the named entities within the input text and their relationships. To generate this graph, we just use off-the-shelf tools (i.e., from the CoreNLP framework) to extract subject-verb-object triplets from the text and perform coreference resolution4 to unify duplicate entities, thus forming a graph representation of our input text.
Encoding the inputs. To ingest data from the different input modalities (i.e., text, image, and graph), we use separate encoders for each. For the image and text data, we can just use a transformer encoder! In [1], images are encoded using a vision transformer [4], while text is encoded using the encoder of the T5 model [5].
Notably, we should realize here that the GOTR framework is using a different model architecture compared to most causal LLMs5. Rather than the typical decoder-only architecture used by causal language models, GOTR uses a prefix-based language modeling approach that ingests input with multiple encoder models, then passes the output of these encoders to a decoder to generate output. This is similar to the encoder-decoder transformer architecture, but there are multiple different types of encoders that are used! To handle the multiple encoders, we have a few learnable layers prior to the decoder that fuse their outputs into a single sequence that is then passed to the decoder. The full encoder-decoder setup used by GOTR is fine-tuned on the desired task.

Using the GAT. The encoder used for the thought graph is based upon a GAT architecture. As mentioned previously, the GAT is a style of GCN architecture. Instead of aggregating features of neighboring nodes via a simple sum or average operation, GATs use an attention mechanism to aggregate information between neighboring nodes. The exact GAT architecture used in [1] is depicted above.
Fusing representations. Once we have encoded the data from our text, image, and thought graph inputs, we need to fuse these features together prior to passing them to the decoder to generate an output. To do this, we can first use a simple cross-attention mechanism! This initial feature fusion operation is shown below, where textual features are fused with both image and thought graph features using cross attention. Here, we should recall that image features are optional and can be completely excluded from the GOTR framework.
After cross-attention, we still have image features, text features, and (potentially) image features. We still need to combine these features together into a single feature representation that can be passed to the decoder. This is done via a gated fusion layer. Although this might sound complicated, all it means is that we i) take our input features, ii) multiply them by some learnable weight matrices, and iii) produce “masks” (i.e., matrices with values between zero and one at each entry) that tell use which portions of each feature to keep or get rid of as we combine all image, text, and graph features together; see below.
Experimental results. The GOTR framework is evaluated on two tasks: text-only GSM8K (i.e., grade-school math problems) and multi-modal ScienceQA (i.e., multiple choice science questions). GOTR uses a pre-trained T5 model [5] as its backbone and DETR [6] as its image encoder. Notably, GOTR is fine-tuned on each of the experimental benchmarks. As such, all baselines that are used for comparison—including few-shot learning and CoT prompting with multiple LLMs, as well as a few task-specific methods—undergo similar fine-tuning prior to evaluation.
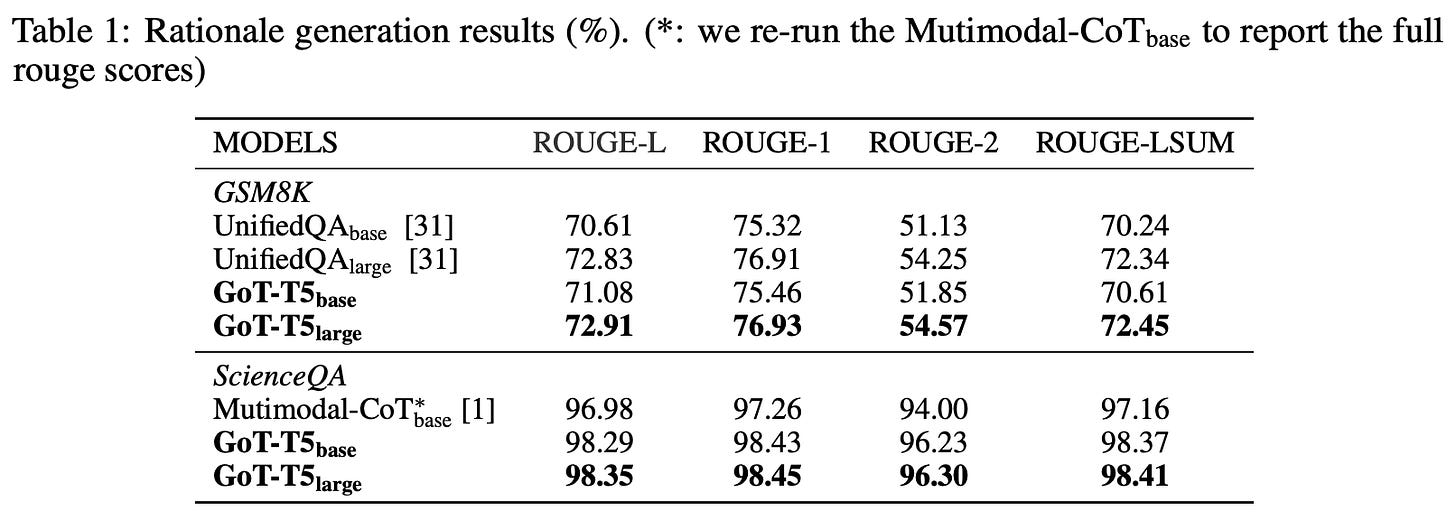
When we solely look at the quality of problem-solving rationales generated by GOTR in comparison to other frameworks, we immediately learn that GOTR generates higher-quality rationales in terms of ROUGE score; see above. Most notably, we see a slight increase in quality compared to multi-modal CoT and UnifiedQA approaches, which seem to indicate that incorporating a thought graph into the problem-solving process can be helpful.
When we examine the accuracy of GOTR’s final solutions, we see that the framework in [1] outperforms a variety of other alternatives on the GSM8K dataset; see above. Notably, GPT-4 far outperforms all other techniques. However, we should keep in mind that such a comparison is likely unfair given that GPT-4 is rumored to be an ensemble (or mixture) of several large models. Plus, GOTR makes significant progress towards closing the gap in performance with GPT-4 and outperforms strong baselines like GPT-3 [7] and GPT-3.5.
On the ScienceQA dataset, GOTR achieves state-of-the-art performance among all techniques, even outperforming GPT-4 with CoT prompting in several cases. Such results indicate that GOTR is a useful framework for integrating multiple modalities of data into the problem-solving process. Although we see a slight improvement in performance on the GSM8K dataset, GOTR’s value is most evident when used for ScienceQA given its ability to leverage all input data modalities—text, image, and graph—when solving a reasoning task.
Graph of Thoughts: Solving Elaborate Problems with Large Language Models [2]
“This work brings the LLM reasoning closer to human thinking or brain mechanisms such as recurrence, both of which form complex networks.” - from [2]
Although GOTR is an interesting framework, one may argue that it is not truly a prompting technique, as it must be fine-tuned or trained to solve any reasoning problem. In [2], authors again explore a graph-inspired framework for reasoning with LLMs. However, a pure prompting approach—similar to CoT [8] or ToT prompting [9]—is taken that i) uses a casual pre-trained LLM and ii) does not require any fine-tuning. The method, called Graph of Thought (GoT) prompting, models each thought generated by an LLM as a node within a graph, then uses vertices that connect these nodes to represent dependencies; see below.
As previously mentioned, humans may not follow a strict chain of thought when solving a problem. Instead, they are likely to:
Try multiple chains of thought.
Combine insights from multiple chains of thought together.
The first case outlined above can be handled by ToT prompting, but combining different chains of thought is not amenable to a tree-structured thought pattern. For this, we need a graph structure in which multiple paths of reasoning can be merged together. Furthermore, such a structure enables patterns like recurrence to be captured, which may be valuable for solving a variety of different problems.
The GoT approach in [1] enables us to model individual thoughts from an LLM and arbitrarily combine these thoughts—e.g., by distilling an entire network of thoughts, enhancing thoughts with feedback loops, and more—to form an accurate output. Plus, the framework is extensible to other models and thought patterns, making plug-and-play with different LLMs and prompting techniques easy.
GoT framework. The approach employed by GoT is shown in the figure above. The LLM’s reasoning process is represented as a (directed) graph. Each node in this graph corresponds to an individual thought generated by an LLM, and edges represent relationships between thoughts. Namely, an edge from thought a to b—or directed edge (a, b) in the graph—simply tells us that thought b was generated using thought a as input. Similarly to ToT prompting, the exact definition of a thought depends on the problem being solved. Going further, each node represents a (potentially intermediate) solution to a problem, but we can have different types of nodes within the graph that represent different aspects of the reasoning process (e.g., planning versus execution).
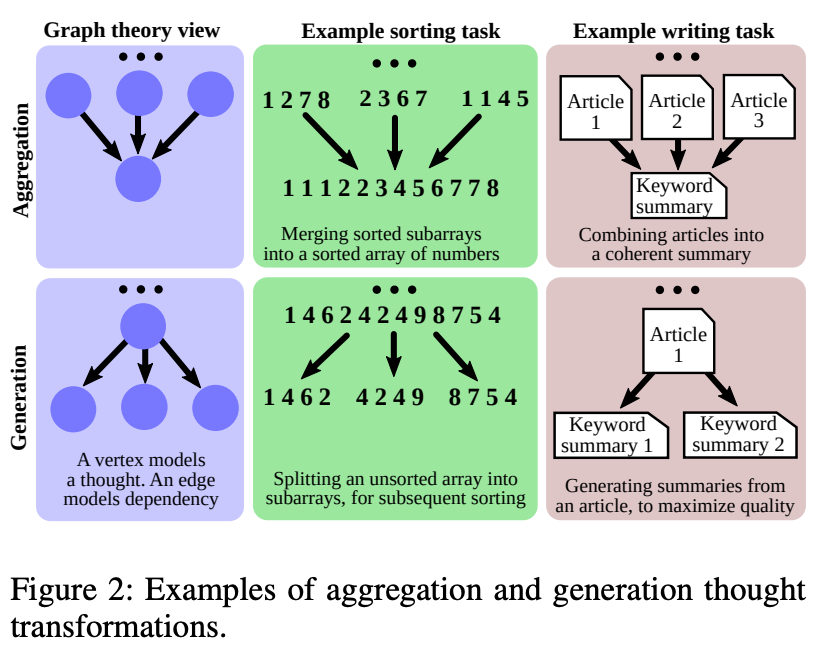
Thought transformations. Given that we use a graph to represent the reasoning process executed by the LLM, any modification to this graph represents a modification to the underlying reasoning process. Authors in [2] refer to these modifications as thought transformations, which are concretely defined as adding new vertices or edges to the graph. As shown in the figure above, various kinds of thought transformations exist (e.g., merging or splitting numbers of an array, summarizing a set of articles, generating multiple summaries of a single article, and so on). We consider three primary types of thought transformations in [2]:
Aggregation: aggregate arbitrary thoughts into a new thought.
Refinement: refining the content in a thought via a self-connection.
Generation: generate multiple new thoughts based on a single thought.
Each of these transformations can modify and advance an LLM’s reasoning process arbitrarily. For example, aggregation can merge the results of multiple different chains of thought together, while refinement can recursively update a thought until arriving at a final answer. Such functionality strictly extends CoT and ToT prompting—it can do everything these techniques can do and more!
“When working on a novel idea, a human would not only follow a chain of thoughts (as in CoT) or try different separate ones (as in ToT), but would actually form a more complex network of thoughts.” - from [2]
Scoring and ranking. Finally, GoT prompting uses evaluator functions to assign scores to certain thoughts, as well as a ranking function to select the most relevant thoughts. Notably, both ranking and scoring consider the entire graph. This is necessary because, for scoring, the quality of a thought might depend on other thoughts. Ranking typically just returns thoughts with the highest scores.
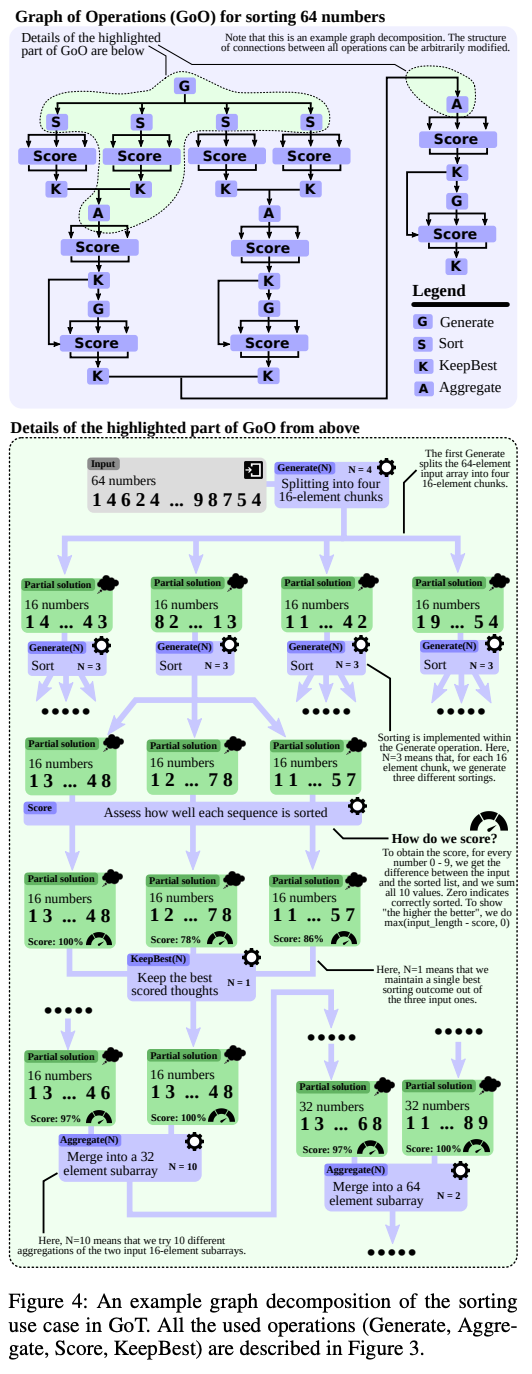
Actual implementation. So far, the discussion of GoT prompting has been relatively high-level, but how do we actually implement this? In [2], authors do this via a series of different LLM-powered modules. The modules, which are detailed in depth in the figure above, are as follows:
Prompter: prepares messages or prompts for the LLM. The prompt is expected to contain an encoding of the graph structure.
Parser: extracts relevant information from LLM outputs, thus forming the state stored within each thought.
Scorer: verifies that thought states satisfy correctness conditions and assigns them a score (derived either from an LLM or a human annotator).
Controller: coordinates the reasoning process and decides how to progress.
Notably, the controller selects the thought transformations that should be applied to the underlying graph, communicates this information to the prompter, and decides whether the reasoning process has finished or should continue forward based on the output of the scorer on generated thought states. Throughout this process, the controller maintains two pieces of information:
Graph of Operations: a user-defined, static structure that is created prior to the reasoning process and captures the execution plan for thought operations.
Graph Reasoning State: a dynamic structure that tracks the state of the LLM reasoning process, including all thoughts and their states.
Use cases. Several applications of GoT prompting are explored in [2]. The first use case is sorting a list of digits (with duplicates) using a merge-based approach6. Here, a thought is defined as a sequence of sorted numbers and thoughts are scored based on the number of errors in the sorting. The full GoT framework for sorting is depicted above. Beyond sorting, authors consider computing the intersection of two sets using GoT prompting, which is also implemented using a merge-based approach. The score of each thought is computed as the number of missing elements from the set intersection. Finally, a few practical use cases, such as keyword counting and document merging (i.e., generating a new output document based on several similar input examples), are considered.
Is GoT effective? To begin their evaluations, authors theoretically analyze two properties of all prompting approaches considered in [2]:
Latency: How many thoughts does it take to reach a solution?
Volume: How many preceding thoughts can impact the current thought?
Interestingly, simple analysis can be used to show that GoT prompting has i) less latency and ii) greater volume compared to prior techniques; see above. When evaluated on sorting tasks, we see that GoT prompting consistently produces fewer errors compared to techniques like CoT [8], CoT with self-consistency [10], or ToT prompting [9]. These results are outlined in the figure below.
One downside of GoT prompting that we see above is that the total cost of deriving a solution is higher than more straightforward approaches like basic few-shot prompting (IO) or CoT. On other tasks, findings are similar; see below.
However, one key takeaway to notice here is that the difference in performance between GoT and other advanced prompting techniques seems to be less pronounced on real-world tasks. For example, GoT prompting provides a less noticeable improvement on the document merging task. Similarly, GoT provides a benefit in terms of performance on the keyword counting task, but baseline techniques—especially ToT prompting—are quite competitive.
When does GoT work well? Within [2], we see that GoT works quite well for certain tasks, but provides less of a benefit on others. When considering whether to use GoT in practice, there are a few questions we should ask:
Can the problem we are trying to solve be easily broken in to smaller, solvable sub-problems and merged for a final solution? For these kinds of (merge-based) problems, GoT prompting works incredibly well.
Is the increased cost of GoT prompting going to be a problem? Can we get a reasonable solution with a cheaper technique (e.g., CoT prompting)?
The answers to these questions will determine whether it makes sense to use GoT prompting. We see in [2] that this method works well, but it also i) is more costly and ii) only has a noticeable impact on performance for certain types of problems.
Takeaways
“Graph-enabled transformations bring a promise of more powerful prompting when applied to LLM thoughts, but they are not naturally expressible with chain of thought or tree of thought prompting.” - from [2]
The techniques we have learned about in this overview are inspired by a simple idea—allowing language models to structure their reasoning process as a graph. Although this idea might seem natural, prior techniques have achieved massive success without it. Despite this success, we see in this overview that moving away from a linear reasoning process towards a more flexible graph-based structure is beneficial on certain tasks. Interestingly, multiple different approaches for “graph of thought” prompting have been explored, including both GOTR—a two-stage reasoning framework that uses an encoder-decoder structure with fine-tuning—and GoT [2]—a more traditional prompting approach that leverages a system of language foundation models with prompts. For both of these techniques, we see that a graph structure can benefit the reasoning process. However, the resulting reasoning process can be more complex and costly, revealing that a GoT-style approach may only be necessary for problems that cannot be solved via standard CoT.
New to the newsletter?
Hi! I’m Cameron R. Wolfe, deep learning Ph.D. and Director of AI at Rebuy. This is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews of relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on Medium, X, and LinkedIn!
Bibliography
[1] Yao, Yao, Zuchao Li, and Hai Zhao. "Beyond Chain-of-Thought, Effective Graph-of-Thought Reasoning in Large Language Models." arXiv preprint arXiv:2305.16582 (2023).
[2] Besta, Maciej, et al. "Graph of Thoughts: Solving Elaborate Problems with Large Language Models." arXiv preprint arXiv:2308.09687 (2023).
[3] Zhang, Zhuosheng, et al. "Multimodal chain-of-thought reasoning in language models." arXiv preprint arXiv:2302.00923 (2023).
[4] Dosovitskiy, Alexey, et al. "An image is worth 16x16 words: Transformers for image recognition at scale." arXiv preprint arXiv:2010.11929 (2020).
[5] Raffel, Colin, et al. "Exploring the limits of transfer learning with a unified text-to-text transformer." The Journal of Machine Learning Research 21.1 (2020): 5485-5551.
[6] Carion, Nicolas, et al. "End-to-end object detection with transformers." European conference on computer vision. Cham: Springer International Publishing, 2020.
[7] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.
[8] Wei, Jason, et al. "Chain-of-thought prompting elicits reasoning in large language models." Advances in Neural Information Processing Systems 35 (2022): 24824-24837.
[9] Yao, Shunyu, et al. "Tree of thoughts: Deliberate problem solving with large language models." arXiv preprint arXiv:2305.10601 (2023).
[10] Wang, Xuezhi, et al. "Self-consistency improves chain of thought reasoning in language models." arXiv preprint arXiv:2203.11171 (2022).
[11] Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
[12] Devlin, Jacob, et al. "Bert: Pre-training of deep bidirectional transformers for language understanding." arXiv preprint arXiv:1810.04805 (2018).
[13] Kipf, Thomas N., and Max Welling. "Semi-supervised classification with graph convolutional networks." arXiv preprint arXiv:1609.02907 (2016).
[14] Veličković, Petar, et al. "Graph attention networks." arXiv preprint arXiv:1710.10903 (2017).
This stands for sequence-to-sequence and refers to tasks that take a sequence as input and produce another sequence as output. For example, language translation tasks take a sequence of tokens in one language and produce the corresponding/translated sequence of tokens in another language as output.
These tasks take a textual prefix as input, then generate a completion. Encoder-decoder models work well for these tasks because the bidirectional self-attention used in the encoder allows a more comprehensive representation of the prefix to be formed before generating output, compared to causal language models that use solely masked self-attention to ingest the prefix.
Notable, the two-stage framework adopted in [1] is inspired by the technique used by multi-modal CoT prompting [3].
Put simply, coreference resolution refers to the problem of finding all noun phrases that refer to the same real-world entity. In [1], we need this to ensure that all nodes in our thought graph are unique! Read more about this idea here.
Here, we use the term “causal LLM” to refer to large language models that use a decoder-only transformer architecture and are trained using a next token prediction (or language modeling) objective.
This means that our approach will divide an array of digits into sub-arrays, sort these sub-arrays, then combine them back together.

























How hard and expensive would it be for a small business to apply what you have discussed here to improve predictions and decision making? Are there open source solutions? Could you be hired to help somebody?