Tree of Thoughts Prompting
Solving multi-step problems with LLMs via deliberate planning and exploration...
This newsletter is presented by Deci AI. Deci does a ton of interesting AI research. Most recently, they released DeciCoder-1B, an open-source code generation model. Read about it here or download it on HuggingFace.
Sponsor the newsletter | Follow me on Twitter | Get in touch | Suggest a topic
As large language models (LLMs) first started to gain in popularity, they were criticized for their shortcomings in solving complex, reasoning-based problems. Although scaling up these models (i.e., more parameters and more data) provided a near-uniform performance improvement across tasks, we saw virtually no boost in performance on reasoning-based tasks with modern LLMs. This changed with the proposal of advanced prompting techniques, such as chain of thought prompting [2] and self-consistency [3]. Such methods showed us that LLMs are more than capable of reasoning and solving complex, multi-step problems. They just have to be properly prompted to fully leverage these abilities.
“It is perhaps surprising that underlying all this progress is still the original autoregressive mechanism for generating text, which makes token-level decisions one by one and in a left-to-right fashion.” - from [1]
Even if proper prompting can enable LLMs to solve complex problems, these techniques are lacking. Namely, we typically i) provide a prompt to the LLM and ii) expect the model to use next token prediction to generate a full solution. Certain approaches may generate solutions in a step-by-step fashion (e.g., least-to-most prompting [8]), but the LLM still follows a single reasoning path instead of exploring several potential solutions. For complex problems in which initial decisions can completely derail a solution, such an approach will fall short, which is an issue given that LLMs are now commonly used as general purpose problem solvers in a variety of practical applications. Put simply, we need a prompting approach that performs more deliberate planning and exploration when solving problems.
In [1], authors propose such an approach—called Tree of Thoughts prompting—that solves problems by explicitly decomposing them into a series of thoughts, or intermediate steps. Similar to chain of thoughts prompting, tree of thoughts prompting generates a solution that is simply a sequence of individual thoughts. However, this approach goes further by allowing multiple reasoning path to be considered at once—forming a tree of potential thoughts or reasoning paths—and exploring this entire solution space via LLM-powered self-evaluation. With tree of thoughts prompting, the LLM can deliberately plan its solution, test various intermediate reasoning paths, and even perform backtracking, allowing the model to explore the solution space and eventually generate the correct output.
Connections to Research in Other Fields and Generations
“A genuine problem-solving process involves the repeated use of available information to initiate exploration, which discloses, in turn, more information until a way to attain the solution is finally discovered.” - from [12]
Analogy to humans. To explain their technique, authors in [1] draw upon analysis of the human decision making process. In particular, humans seems to have two separate modes of making decisions:
A fast, automatic, and unconscious mode
A slow, deliberate, conscious mode
Authors in [1] argue that techniques like chain of thought prompting seem to mimic the first mode outlined above, as the LLM just generates text in a left-to-right manner without deliberate planning or deconstruction of the problem. The main motivation behind tree of thoughts prompting is to inject deliberate planning and exploration into the problem-solving process by deconstructing each problem into a tree of smaller steps that are individually explored.
Inspired by early work in AI. The planning process followed by tree of thoughts prompting is inspired by AI research from the mid 20th century [12, 13]! This work argues that problem solving can be formulated as searching through a combinatorial space represented as a tree. Within this space, multiple active chains of thought are maintained, each representing an individual path within the larger tree. As we will see, this formulation allows us to explicitly decompose a solution to a complex problem, as well as leverage established graph algorithms (e.g., breadth-first and depth-first search) to find a viable solution.
The Basics of Prompting
The generic text-to-text format of LLMs is incredibly powerful. To solve any problem, we can simply i) write a textual prompt that describes the problem and ii) generate a relevant output/solution with the language model. For this reason, LLMs are considered to be foundation models, or models that can singlehandedly be adapted to solve a wide variety of tasks. Such an ability is largely due to in-context learning. Namely, pre-trained LLMs have the ability to use data injected into their prompt as context to produce a more accurate output; see below.
However, the effectiveness of in-context learning is highly related to the prompt that is used to solve a problem. Many different prompting approaches—including tree of thoughts prompting [1]—exist, but the process of choosing the correct prompting technique or writing the correct prompt can be quite difficult. For this reason, we will now take a brief look at the basics of prompt engineering, providing useful context that will make the various prompting techniques explored within this overview more understandable.
What is prompt engineering?
“Prompt engineering is a relatively new discipline for developing and optimizing prompts to efficiently use LMs for a wide variety of applications and research topics.” - from [2]
Prompt engineering refers to the process of iteratively tweaking a prompt for a language model with the goal of discovering a prompt that accurately solves a desired task. Typically, the prompt engineering process is empirical, meaning that we discover the best prompts by measuring their performance on related tasks. Prompting is a new field that is full of heuristics and a variety of different techniques. As such, we can maximizes our chances of success by following an approach similar to any other engineering problem:
Track and version different prompts
Setup extensive benchmarks to measure prompt performance
Test different ideas to see what yields the best results
Context window. One major consideration when writing a prompt is the size of the underlying LLM’s context window. As shown in the figure above, all LLMs are trained using inputs of a certain size (i.e., referred to as the size of the context window or context length), which—along with memory constraints—limits the total amount of data that can be provided to an LLM within a prompt. Practically, this means that we must be selective about the data that is included in a prompt1. Next, we will overview the components of a prompt, as well as the kinds of information that might be provided to guide an LLM towards a correct solution.
Structure of a Prompt
A variety of prompting techniques exist, but each of these techniques utilize a (relatively) common structure. The various components of prompts that one might encounter are depicted within the figure above and outlined below.
Input Data: the input data being processed by the LLM.
Exemplars: input-output examples that demonstrate correctly solving a desired problem.
Instruction: a detailed, textual description of the LLM’s expected behavior.
Indicators: textual tags that are used to organize and structure the different components of a prompt.
Context: any extra context that may be useful to provide to the LLM (e.g., chunks of information retrieved from a vector database).
Notably, not all of these components are necessary when writing a prompt. Several of the techniques explored in this overview will only use a subset of the above components, but each of them can be leveraged to provide extra, useful information to the LLM when necessary.
Hierarchy of Prompting Techniques

Now that we have a basic understanding of in-context learning and prompt engineering, we need to take a deeper dive into some common techniques for prompting a language model. We will start with simpler techniques, such as zero and few-shot prompting, then move on to more complex techniques like chain of thought prompting [2] and self-consistency [3]. As always, we should remember that simplicity is best when writing prompts—we should start as simple as possible, then use test-driven development to decide when extra complexity is necessary. In other words, we can create a large benchmark of prompt examples based upon our desired application, then measure performance on this benchmark as we iterate and test different prompting variants. For a more extensive (and practical) guide on prompting, check out the article below.
Zero and Few-Shot Prompting
Zero-shot prompting is one of the simplest techniques that we can use for prompting a language model and originally became popular when leveraged by GPT-2 to achieve impressive performance across a wide variety of different natural language benchmarks. To form a zero-shot prompt, we need to provide two pieces of information (see above):
A task description
Our input data
Here, the language model is expected to leverage its knowledge base and the provided task description to solve a problem without any explicit exemplars or detailed instructions. Although many language models can perform relatively well when prompted in a zero-shot manner, we typically need to provide extra details to the model to get more reliable and accurate results.
Few-shot prompting goes beyond zero-shot prompting by adding “exemplars” of the model’s desired output to the prompt; see above. In addition to a task description, we provide several examples of correct input-output pairs. By adding this context to the prompt, we can provide the language model with more concrete details about the output that is expected. This technique was popularized with GPT-3 [5], where language models were first shown to be highly capable in-context learners. Put simply, the model can learn from these exemplars and improve in accuracy as more are provided.
Instruction Prompting
Zero and few-shot learning are simple techniques that work surprisingly well, but sometimes they will not yield sufficient levels of performance. Plus, few-shot learning has the added limitation of increasing the size of the prompt2. If these techniques are not working for our use case, the next technique we can try is instruction prompting. Instead of demonstrating correct behavior via a task description and several examples of correct output, instruction prompting includes a detailed instruction—or explanation of the correct behavior—within the prompt that is given to the language model; see below.
Plus, instruction prompting and few-shot prompting are not mutually exclusive! We can easily combine an instruction prompt with several few-shot exemplars to yield improved performance. In fact, the task descriptions used by zero and few-shot prompting techniques are actually quite similar to an instruction anyways.
Alignment is necessary. Crafting thoughtful instructions is a highly effective and token-efficient prompting technique. However, not all language models are good instruction followers. For example, pre-trained (base) LLMs do not naturally have the ability to follow detailed instructions. This ability is typically developed via an alignment process that fine-tunes the LLM’s ability to follow instructions; see above. Many modern LLMs (e.g., GPT-4) are incredibly steerable (i.e., adept at following detailed instructions), making instruction prompting one of the most effective techniques for working with such models, as shown below.
Advanced Prompting Techniques
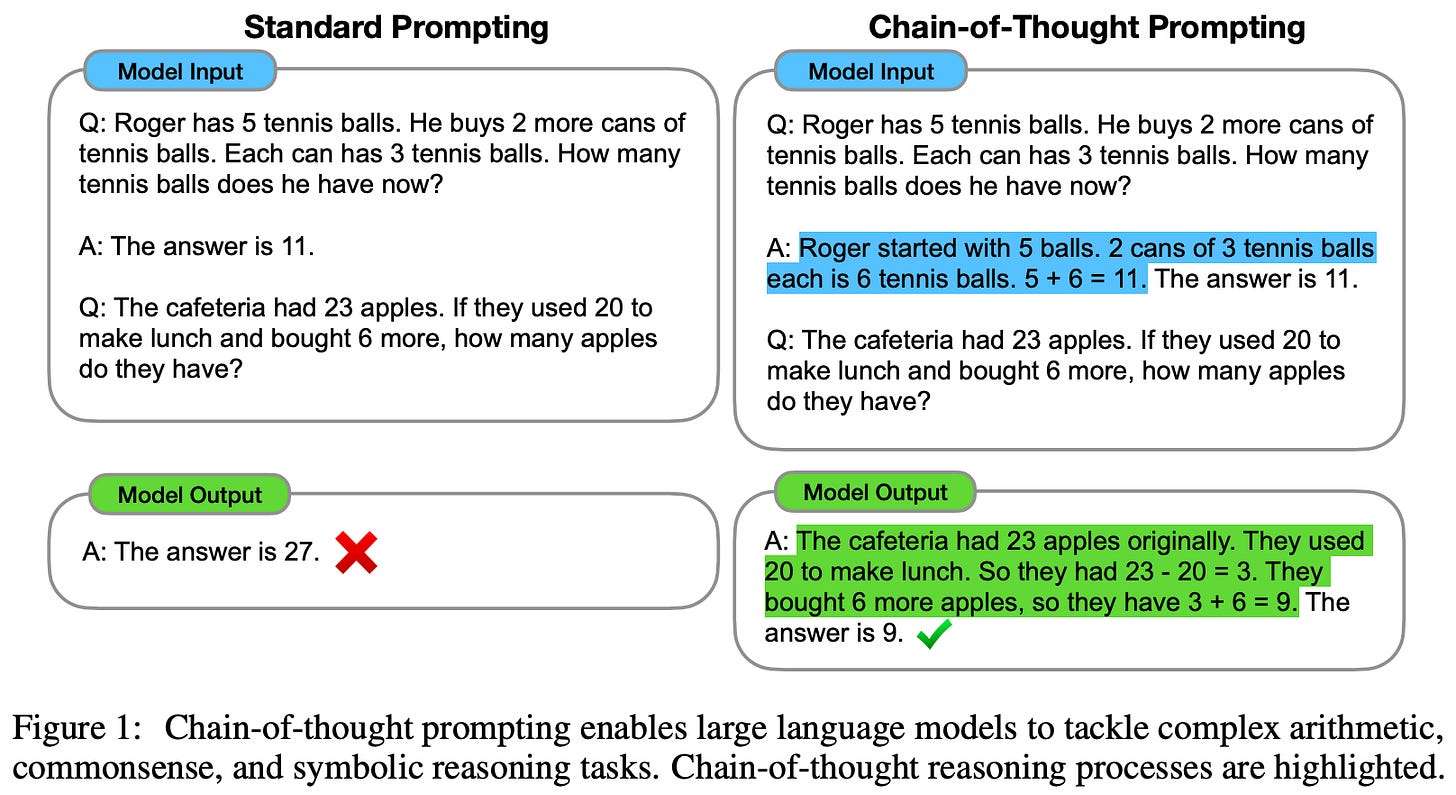
Sometimes, few-shot and instruction prompting are not enough to accomplish a desired task. In particular, language models tend to struggle with complex reasoning problems, such as commonsense reasoning problems that require multiple steps or mathematical puzzles. However, numerous advanced prompting techniques—including tree of thoughts prompting—have been developed to expand the scope of difficult problems that can be solved with an LLM. In this section, we will focus on one technique—chain of thought (CoT) prompting [2] (and its several variants)—that is especially effective in practice and forms the basis of the methodology used for tree of thoughts prompting.
What is CoT prompting? By leveraging in-context learning abilities, CoT prompting encourages a language model to more effectively solve complex problems by outputting along with its solution a corresponding “chain of thought” (i.e., a step-by-step explanation for how the problem was solved). The model can be prompted to generate a chain of thought via a few-shot learning approach that provides several chain of thought exemplars; see above. The CoT technique is most effective when the map from input to output is highly non-trivial; e.g., math or multi-step reasoning problems. In such cases, introducing a chain of thought allows the model to follow smaller, intermediate steps towards the correct final solution. In practice, CoT prompting was found to drastically improve LLM performance on various styles of reasoning tasks; see below.
Variants of CoT prompting. Given the practical utility of CoT prompting (i.e., it can be used to solve complex, multi-step problems with which LLMs typically struggle!), several variants of this technique were developed shortly after its proposal, such as zero-shot CoT [7] and least-to-most prompting [8]; see below.
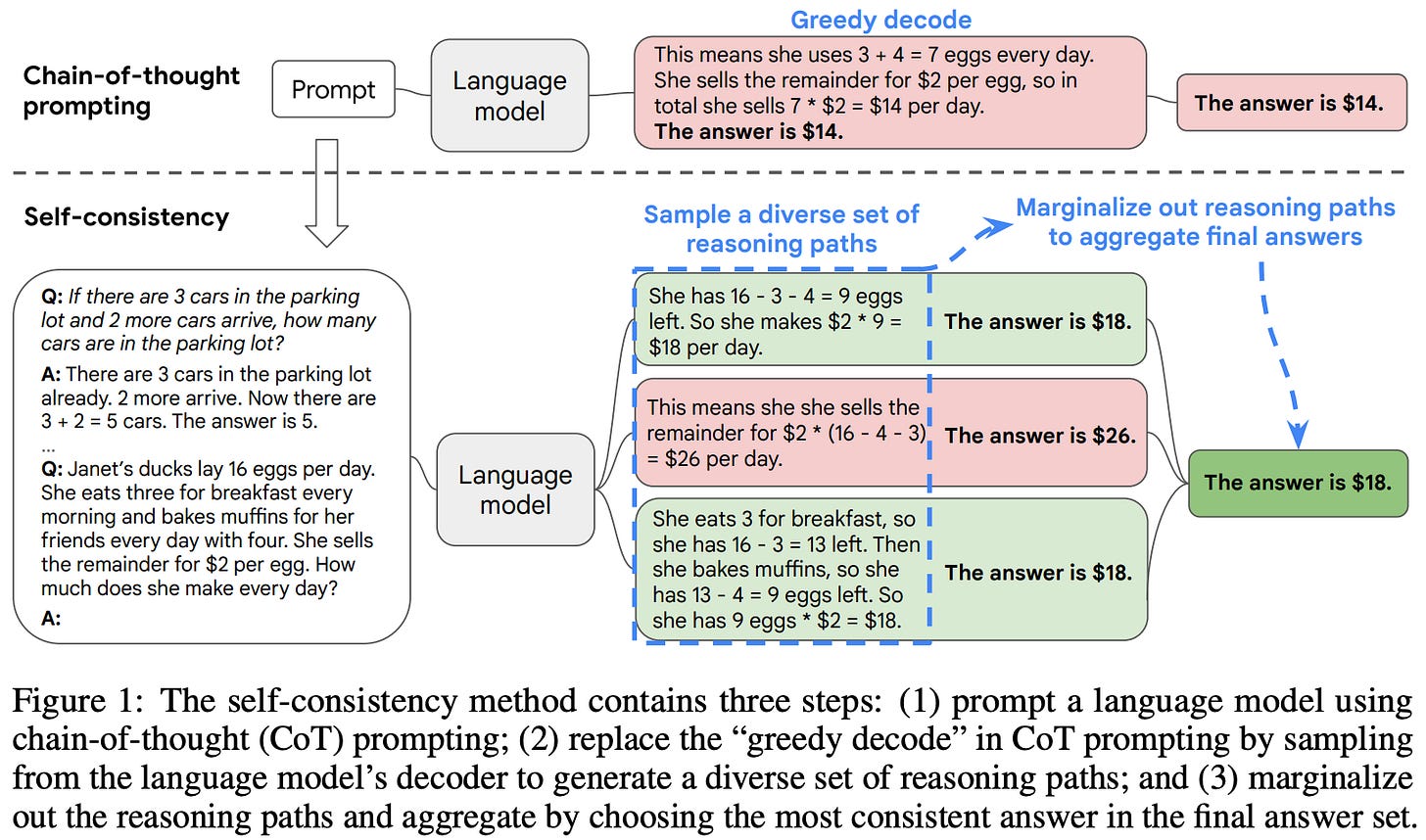
The CoT prompting variant that is most relevant to tree of thought prompting is self-consistency [3]. This approach leverages an approach that is similar to that of CoT prompting. A single model is prompted—using the same (CoT) prompt—to generate output several different times. Then, the final answer is generated by taking a majority vote of the model’s outputs as shown in the figure below. Such an approach is found to yield similar benefits to CoT prompting, as well as improve performance and reliability on more difficult problems.
Existing limitations. Techniques like CoT prompting and self-consistency do a lot to expand the scope of problems that are solvable with LLMs. Without them, solving multi-step reasoning problems would be quite difficult. However, these prompting techniques do not come without limitations. For example, not all problems have a solution space that is amenable to a majority vote, and a majority vote has been shown in prior work to be a poor heuristic for improving LLM accuracy even for problems that can be formulated in this manner.
“We see 9.5% average variation in accuracy and that the Jaccard index over errors is 69% higher than if prompt errors were i.i.d. Majority vote (MV) is the primary unsupervised aggregation strategy in prior work but it does not account for either property, making it unreliable.” - from [9]
More broadly, solving a complex task may require extensive planning, strategic lookahead, backtracking, and even exploration of numerous viable solutions in parallel. Techniques like CoT prompting follow a left-to-right, continuous generation approach that uses next-token prediction to output a solution in a single attempt. Such an approach, although highly effective in certain scenarios, fails to solve tasks that require strategic planning and exploration. But, this is where tree of thoughts prompting comes in! Similar to CoT prompting, tree of thoughts prompting breaks problems down into smaller parts (i.e., a chain of thought) but goes further by combining this with the ability to explore multiple solution paths in parallel, forming a tree instead of a single chain!
Understanding Tree of Thoughts Prompting
The effectiveness of CoT prompting comes from its ability to break a complex problem solution into a sequence of smaller and simpler steps. Tree of thoughts (ToT) prompting similarly breaks a problem into a sequence of smaller steps—or thoughts—that are solved individually. However, the approach does not constrain the model to output these steps all at once. Rather, each thought is generated or solved independently and passed to the next step for solving the problem, which allows the model to:
Explore multiple choices for each problem-solving thought.
Evaluate whether certain thoughts bring the model closer to a final solution.
Perform backtracking when certain thoughts are found to be a dead end.
Search over a combinatorial space of possible problem-solving steps to find the best final solution.
With ToT prompting, an entire tree of thoughts (shown above) is formed by allowing exploration of different thoughts throughout the problem-solving process. During exploration, the LLM can evaluate progress made by each thought towards a final solution via a language-based process3. Then, by leveraging widely-used search algorithms (e.g., breadth-first search or depth-first search), ToT prompting can be augmented with lookahead and backtracking techniques, allowing the solution space of any problem to be thoroughly explored.
“While existing methods sample continuous language sequences for problem solving, ToT actively maintains a tree of thoughts, where each thought is a coherent language sequence that serves as an intermediate step toward problem solving.” - from [1]
What does the tree represent? When using ToT prompting, we explore several paths—each comprised of individual thoughts—that represent potential solutions to a problem. Together, each of these paths and their individual thoughts form a tree that explores a problem’s solution space; see above. In this tree, each node is simply a partial solution (or thought) to our problem, while each connection is a operator that modifies this partial solution to yield the next thought within a problem-solving path. An example of decomposing a problem-solving chain of thought (i.e., a single path in a tree of thoughts) in this way is shown below.
Tree of Thoughts Problem Solving Framework
At this point, we have talked about the generic idea behind ToT prompting, but how do we use this technique in a practical application? The implementation of ToT prompting looks a bit different depending upon the problem we are trying to solve, but any instantiation of ToT prompting has to concretely define four standard problem-solving components, which are outlined below.
Thought decomposition. Unlike CoT prompting, ToT explicitly decomposes a problem into intermediate steps or thoughts, which are combined together to form a solution to the underlying problem. Depending on the problem, this decomposition can take a variety of different forms, such as outputting a few words or a single line of an equation. As shown above, the definition of a thought is different for each of the three separate tasks that are considered in [1].
“A thought should be small enough so that LMs can generate promising and diverse samples (e.g. generating a whole book is usually too big to be coherent), yet big enough so that LMs can evaluate its prospect toward problem solving (e.g. generating one token is usually too small to evaluate).” - from [1]
Thought generation. Once we have decided what will constitute a thought, we need to determine how thoughts should be generated during ToT prompting. In [1], authors propose two basic techniques for thought generation:
Sampling: generating several thoughts independently with the same prompt
Proposing: generating several thoughts sequentially with a “propose prompt”
The sampling approach works best when the thought space is rich, as several independently-generated thoughts are unlikely to be duplicates. If the thought space is more constrained, then the proposing technique can be used to generate several thoughts while avoiding duplicates.
State evaluation. Once we have defined our thoughts and chosen how they will be generated, we need to define a heuristic for evaluating the quality of certain chains of thought. Otherwise, there is no way to know whether we are making progress towards a final solution. Given several thoughts that have been generated, authors in [1] use an LLM to reason about the quality of each thought. In particular, two different strategies are followed:
Value: independently assign a scalar value (i.e., rating from 1-10) or classification (i.e., sure, likely, or impossible to reach a solution) to each state.
Vote: compare different solutions and select the one that is most promising.
Although both approaches can work well, voting is best when a successful solution to a problem is hard to directly value (e.g., creative writing tasks). In both cases, the LLM can be prompted multiple times in a manner similar to self-consistency to achieve more reliable evaluations of each state.
Search algorithm. The final component of ToT prompting is the search algorithm that is used to explore the solution space. Although many potential search algorithms can be used, we see in [1] that authors focus on two basic algorithms—BFS and DFS—with formulations shown above.
Experimental Analysis
Authors in [1] propose three new tasks that are used to evaluate the ToT prompting technique: Game of 24, Creative Writing, and 5x5 Crosswords. For each of these tasks, we will first overview the implementation of ToT prompting, which follows the four-part framework outlined above. Then, we will outline the experimental results, highlighting the effectiveness of ToT prompting on problems that require extensive planning or search. Notably, alternatives like CoT prompting and self-consistency tend to fall short of solving such complex tasks.
Game of 24
The implementation of ToT prompting for the Game of 24 task is shown above. In this task, the LLM is given four numbers and expected to generate a sequence of arithmetic operations—where each number is only used once—that result in the number 24. This task is always decomposed into three thoughts4, each of which is an intermediate equation. The same prompt is used to generate each of the three thoughts in a candidate solution, and we evaluate states with a value prompt that classifies intermediate solutions as sure, likely, or impossible to reach a correct final solution. Then, a BFS algorithm is applied to find the resulting solution, keeping the best five (i.e., b=5) candidate solutions at each step.
Performance. ToT prompting is compared to several baselines, including standard few-shot prompting (IO), CoT prompting, and CoT-based self-consistency (CoT-SC). As shown above, all baselines perform quite poorly on this task (i.e., <10% success rate), while ToT prompting achieves up to a 74% success rate. Interestingly, the success rate improves with higher settings of b for BFS. Furthermore, we see based on error analysis in [1] that most solutions with CoT prompting fail after the first step, while failures with ToT prompting are distributed uniformly among intermediate steps. Such a finding demonstrates the benefit of ToT prompting, as it can evaluate intermediate states prior to producing a final output, allowing multiple viable solution paths to be explored.
Creative Writing
The creative writing task explored in [1] provides four random sentences as input to the LLM and expects a passage containing four paragraphs that each end in the four input sentences to be outputted. The quality of outputs is judged either using GPT-4 (with a zero-shot prompt) or human evaluations. For this task, ToT prompting requires two intermediate thoughts. First, the LLM generates five different writing plans and uses a zero-shot voting prompt to select the best one. Then, five different passages are generated based upon the selected plan, and the best passage is identified by using (again) a zero-shot voting prompt; see above.
Performance. As shown in the figure above, ToT generates more coherent passages than few-shot and CoT prompting on average, as judged by both GPT-4 and human evaluators. When an iterative refinement procedure is applied to improve result quality, we see that both few-shot and ToT prompting perform comparably. Such a procedure can be thought of as a new approach to thought generation, where new thoughts are generated by prompting the LLM to refine old thoughts instead of generating them from scratch.
5x5 Crosswords
The final task considered in [1] is a mini crossword puzzle, which explores the ability of ToT prompting to discover solutions to problems that require a greater number of intermediate steps. The input for this task provides five horizontal clues and five vertical clues, while the output should be a 5x5 grid of letters that solve the crossword puzzle. Success is judged based upon the portion of correct letters, words, and games achieved by each prompting technique.
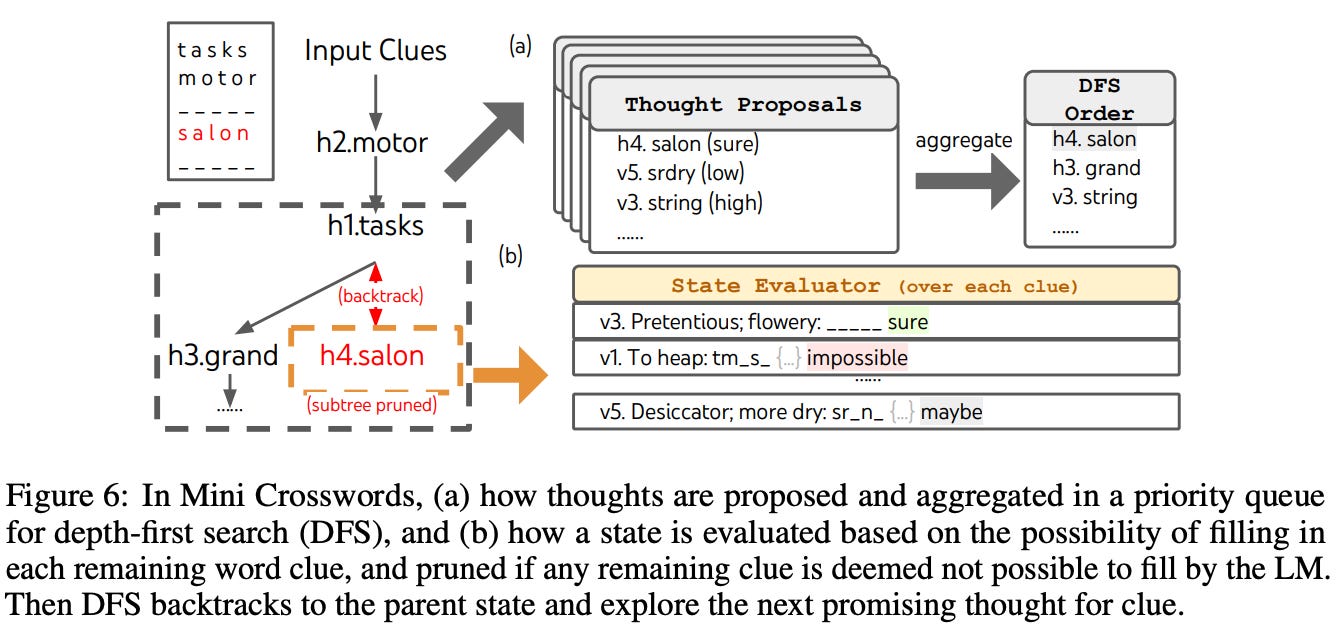
ToT setup. For mini crossword, ToT prompting is implemented with DFS. Each thought considers a single word clue. Thoughts are generated sequentially and cannot change any currently-filled words or letters. To find new candidates, the LLM takes all existing thoughts as input, generates letter constraints for remaining word clues based on these thoughts, and uses a proposal prompt to come up with candidates for the word should be filled next and where it should go. Interestingly, the LLM is also prompted to provide a confidence level for each thought, allowing thoughts to be explored in order of confidence. Intermediate states are evaluated based upon whether it is possible to arrive at a viable final solution. If not, DFS backtracks to the parent node within the tree of thoughts and continues to explore. This entire process is depicted in the figure above.
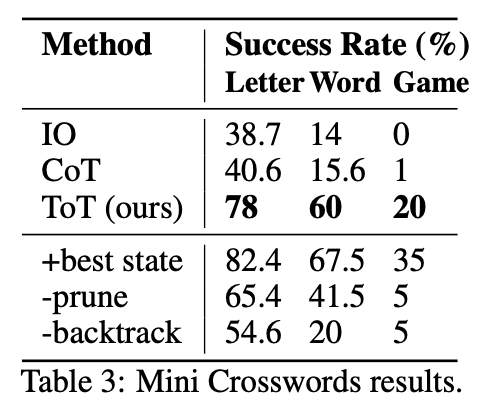
Performance. As shown in the table above, ToT prompting drastically outperforms few-shot and CoT prompting in terms of success rate on the mini crosswords benchmark. Even still, ToT prompting only globally solves 4 out of 20 total puzzles that were tested, revealing that there is significant room for improvement on such tasks. However, the ability of ToT prompting to backtrack and explore different solutions via DFS is a massive differentiator.
“Such an improvement is not surprising, given IO and CoT lack mechanisms to try different clues, make changes to decisions, or backtrack.” - from [1]
Closing Remarks
Recent research on prompting techniques has drastically expanded the scope of problems that are solvable via an LLM. However, most prompting techniques are constrained by the autoregressive nature of language generation—they tend to follow a left-to-right approach that lacks deliberate planning and opportunities for exploring alternative solutions to a problem. ToT prompting solves this issue by abstracting the solution to a problem as a tree of intermediate steps that can be independently explored and evaluated using known algorithms and heuristics. The idea behind ToT prompting is incredibly generic and can be instantiated differently depending on the underlying problem. We see several examples of this in [1], where ToT prompting is shown to more effectively solve multi-step reasoning problems compared to CoT prompting and related variants.
New to the newsletter?
Hi! I’m Cameron R. Wolfe, deep learning Ph.D. and Director of AI at Rebuy. This is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews that explain relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on twitter or LinkedIn!
Bibliography
[1] Yao, Shunyu, et al. "Tree of thoughts: Deliberate problem solving with large language models." arXiv preprint arXiv:2305.10601 (2023).
[2] Wei, Jason, et al. "Chain-of-thought prompting elicits reasoning in large language models." Advances in Neural Information Processing Systems 35 (2022): 24824-24837.
[3] Wang, Xuezhi, et al. "Self-consistency improves chain of thought reasoning in language models." arXiv preprint arXiv:2203.11171 (2022).
[4] Radford, Alec, et al. "Language Models are Unsupervised Multitask Learners."
[5] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.
[6] Ouyang, Long, et al. "Training language models to follow instructions with human feedback." Advances in Neural Information Processing Systems 35 (2022): 27730-27744.
[7] Kojima, Takeshi, et al. "Large language models are zero-shot reasoners." Advances in neural information processing systems 35 (2022): 22199-22213.
[8] Zhou, Denny, et al. "Least-to-most prompting enables complex reasoning in large language models." arXiv preprint arXiv:2205.10625 (2022).
[9] Arora, Simran, et al. "Ask me anything: A simple strategy for prompting language models." arXiv preprint arXiv:2210.02441 (2022).
[10] Raffel, Colin, et al. "Exploring the limits of transfer learning with a unified text-to-text transformer." The Journal of Machine Learning Research 21.1 (2020): 5485-5551.
[11] Saravia, Elvis, et al. “Prompt Engineering Guide”, https://github.com/dair-ai/Prompt-Engineering-Guide (2022).
[12] A. Newell, J. C. Shaw, and H. A. Simon. Report on a general problem solving program. In IFIP congress, volume 256, page 64. Pittsburgh, PA, 1959.
[13] A. Newell, H. A. Simon, et al. Human problem solving. Prentice-Hall, 1972.
Plus, using a longer prompt results in higher usage on LLM APIs due to the increased number of tokens. Even when using open-source LLMs, longer prompts are likely to lead to heightened inference times.
If we are using an API, then we have to pay for usage based on the number of tokens or characters that the model ingests and generates. As such, using many few-shot exemplars in our prompt can drastically increase the number of input tokens and, in turn, increase the price of using the API.
In other words, we can just use a prompting approach that asks the language model—using a standard language-based/textual prompt—to assess its progress towards a final solution for any given problem.
Given that the solution is always an arithmetic equation with four numbers, we know that only three intermediate equations or arithmetic operations always need to be outputted before reaching a final solution.

























Regarding the points on advanced prompting, it's realy fascinating how much mileage we're getting from what's essentially still an autoregressive next-token prediction. Thanks for articulating this so well; it sometimes feels like we're just learning to speak LLM-ese, but with profound results for complex reasoning.