Proximal Policy Optimization (PPO): The Key to LLM Alignment
Modern policy gradient algorithms and their application to language models...
[November 2025] A modernized and LLM-centric version of this post has been published here that more comprehensively covers recent research in RL.
Recent AI research has revealed that reinforcement learning (RL)—reinforcement learning from human feedback (RLHF) in particular—is a key component of training large language models (LLMs). However, many AI practitioners (admittedly) avoid the use of RL due to several factors, including a lack of familiarity with RL or preference for supervised learning techniques. There are valid arguments against the use of RL; e.g., the curation of human preference data is expensive and RL can be data inefficient. However, we should not avoid using RL simply due to a lack of understanding or familiarity! These techniques are not difficult to grasp and, as shown by a variety of recent papers, can massively benefit LLM performance.
This overview is part three in a series that aims to demystify RL and how it is used to train LLMs. Although we have mostly covered fundamental ideas related to RL up until this point, we will now dive into the algorithm that lays the foundation for language model alignment—Proximal Policy Optimization (PPO) [2]. As we will see, PPO works well and is incredibly easy to understand and use, making it a desirable algorithm from a practical perspective. For these reasons, PPO was originally selected in the implementation of RLHF used by OpenAI to align InstructGPT [6]. Shortly after, the popularization of InstructGPT’s sister model—ChatGPT—led both RLHF and PPO to become highly popular.
Background Information
In this series, we are currently learning about reinforcement learning (RL) fundamentals with the goal of understanding the mechanics of language model alignment. More specifically, we want to learn exactly how reinforcement learning from human feedback (RLHF) works. Given that many AI practitioners tend to avoid RL due to being more familiar with supervised learning, deeply understanding RLHF will add a new tool to any practitioner’s belt. Plus, research has demonstrated that RLHF is a pivotal aspect of the alignment process [8]—just using supervised fine-tuning (SFT) is not enough1; see below.
In this section, we will briefly cover the RL algorithms we’ve learned about in this series so far, focusing upon their limitations and the primary reasons why better algorithms are needed. Then, we will (once again) overview the problem setup of RL for language model alignment, which we should use as relevant context when learning about new algorithms. Finally, we’ll learn about the KL divergence, which is a useful concept for both RL and machine learning in general.
What we have learned so far?
Until this point, our overviews within this series have mostly focused on fundamental concepts within RL, including:
Basics of RL for LLMs [link]: problem setup (with extensions to LLMs) and basic algorithms like (Deep) Q-Learning.
Policy Optimization [link]: understanding policy gradients—the class of optimization techniques used by RLHF—and basic algorithms in this space.
Within this post, we will build on these basic concepts by diving into two RL algorithms that are more directly related to RLHF: Trust Region Policy Optimization (TRPO) [1] and Proximal Policy Optimization (PPO) [2]. Similarly to the vanilla policy gradient algorithm that we saw in a prior overview, both of these algorithms are based upon policy gradients. However, PPO, which is an extension of TRPO, is the most commonly used RL algorithm for RLHF [6]!
Why do we need a new algorithm? So far, we have seen two main RL algorithms that can be used to train neural networks (see above):
Deep Q-Learning (DQL) [link]
Vanilla Policy Gradient Algorithm (VPG) [link]
However, these algorithms have notable limitations when used to solve complex problems. DQL can only be applied in relatively simple environments (e.g., game environments like Atari). Despite being effective for problems with discrete action spaces, DQL struggles to generalize to more realistic (continuous action space2) environments, where it is known to fail at solving even simple problems. Going further, VPG has poor data efficiency and robustness, meaning that we must collect tons of data from our environment to eliminate noise within the policy gradient estimate and, in turn, effectively train the underlying policy.
“There is room for improvement in developing a method that is scalable (to large models and parallel implementations), data efficient, and robust (i.e., successful on a variety of problems without hyperparameter tuning).” - from [2]
With this in mind, the motivation behind TRPO and PPO is to improve upon these issues. Namely, we want to derive an RL algorithm that is:
Generally applicable (i.e., to both discrete and continuous problems)
Data efficient
Robust (i.e., works without too much tuning)
Simple (i.e., not too difficult to understand/implement)
TRPO satisfies the first two points outlined above, while PPO satisfies all four. Due to its simplicity and effectiveness, PPO is widely used across domains and has become the go-to choice for aligning language models via RLHF.
Aligning Language Models with RL
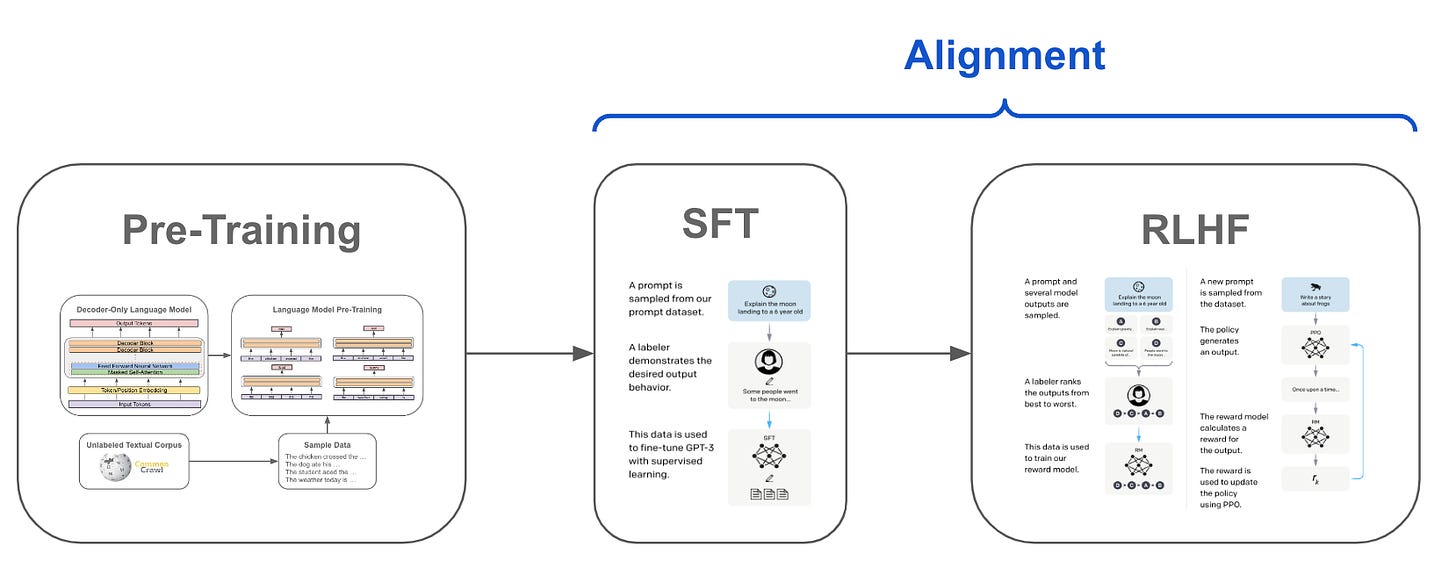
Most modern language models are trained in several phases; see above. First, we perform pretraining, which is the most computationally expensive component of the training process. After pretraining, the LLM can accurately perform next token prediction, but its output may be repetitive, uninteresting, or not useful. To solve this, we can finetune the model to improve its alignment, or ability to generate text that aligns with the desires of a human user.
“Making language models bigger does not inherently make them better at following a user’s intent. For example, large language models can generate outputs that are untruthful, toxic, or simply not helpful to the user. In other words, these models are not aligned with their users.” - from [6]
Typically, we perform alignment by first selecting several alignment criteria (e.g., follow instructions, avoid harmful output, avoid hallucination, produce interesting/creative output, etc.), then finetuning the model—via SFT and RLHF (shown below)—to satisfy these criteria. Once the alignment process is complete, the final model can further finetuned and used to solve a downstream application via prompting (or in-context learning).
Applying RLHF. As its name indicates, RLHF (depicted above) relies upon RL to train a language model from human feedback. We start with a set of prompts and generate several outputs for each prompt with the language model. From here, we ask a group of human annotators to rank/score the responses to each prompt according to our alignment criteria. Using these ranked responses, we can train a reward model that predicts a human preference score from a language model’s response. Then, we can use PPO3 to finetune our language model to maximize the human preferences scores (predicted by the reward model) of its outputs.
Alignment with RL. Obviously, the language model alignment domain is slightly different from the typical RL setup that we have learned about. However, the components of RL actually generalize quite well to language models! To generate text, language models follow an autoregressive process of iteratively predicting the next token and adding this predicted token to the input sequence; see below.
From the lens of RL, our language model is the policy in this case. Given the current state (the textual input sequence), the language model produces an action4—the next token—that modifies the current state by adding a token to the current sequence. Once a full textual sequence has been produced, we can obtain a reward by rating the quality of the language model’s output with the reward model. To finetune the model with RL, we simply alternate between collecting data from the environment—done by generating text with the language model then scoring it with the reward model—and updating the policy according to the update rule defined by our RL algorithm of choice (e.g., VPG, TRPO, or PPO).
Kullback–Leibler (KL) Divergence
At the highest level, the Kullback-Leibler (KL) Divergence is just a method of comparing two probability distributions. The idea of KL divergence has its roots in information theory and is highly related to the concept of entropy. In the equation above, we can see common formulations of entropy for a probability distribution p. Intuitively, the entropy value captures how much information is stored within a probability distribution—a lower entropy means that you would need fewer bits to encode the information stored within p.
KL divergence formulation. Instead of a single probability distribution p, the KL divergence considers two probability distributions: p and q. Then, mirroring the above entropy formulation, we compute KL divergence by finding the expected difference in log probabilities between these two distributions; see below.
The KL divergence is commonly explained in the context of approximations. Namely, if we approximate p with q, the KL divergence is the number of bits we would expect to lose by making this approximation. For more details on the information theory perspective of KL divergence, see the article below.
Applications to AI/ML. KL divergence is heavily used across different domains of AI/ML research. For example, it is commonly used in loss functions for training neural networks, either as the core loss or as an added regularization term. For example, Variational Autoencoders (VAEs) use the KL divergence to encourage similarity between the predicted latent distribution and a prior distribution.
The final reward function we use during optimization contains a [KL divergence] penalty term … we find this constraint is useful for training stability, and to reduce reward hacking.” - from [8]
Furthermore, KL divergence is used heavily within RL research. Here, we will see this concept used in the definition of TRPO, as well as to explain the intuition behind PPO’s update rule. Additionally, most implementations of RLHF add an extra KL divergence term to their loss function, which helps to prevent reward hacking and ensures updates to the language model’s policy are not too large.
Better Algorithms for Reinforcement Learning
Within this section, we will learn about two new RL algorithms, called Trust Region Policy Optimization [1] and Proximal Policy Optimization (PPO) [2] that improve upon the algorithms we have learned about so far. Notably, TRPO and PPO both have drastically improved data efficiency, allowing us to train an effective policy faster and with less data. Going further, PPO is quite simple and robust compared to TRPO, leading to its use in a variety of popular domains.
Trust Region Policy Optimization (TRPO) [1]
We should recall that VPG is limited by the fact that it can only perform a single policy update for each estimate of the policy gradient that is derived. Given that VPG is notoriously data inefficient, meaning that we have to sample a lot of data when deriving a policy update, performing multiple (or larger) updates may seem enticing. However, such an approach is not justified theoretically and, in practice, leads to policy updates that are too large, thus damaging performance.
“While it is appealing to perform multiple steps of optimization on this loss using the same trajectory, doing so is not well-justified, and empirically it often leads to destructively large policy updates” - from [2]
Trust Region Policy Optimization (TRPO) [1] aims to solve the problem described above using an approach that is similar to VPG. At each step of the optimization process, however, we find the largest possible policy update that still improves performance. Put simply, TRPO allows us to learn faster by finding a reliable way to make larger policy updates that do not damage performance.
TRPO formulation. More specifically, we update the policy under a constraint—based on the KL divergence—that captures the distance between policies before and after the current update. Considering this constraint allows us to find a balance between update size and the amount of change to the underlying policy.
To make this discussion a bit more concrete, the theoretical update rule used by TRPO is shown within the equation above. Here, the advantage function is computed using some advantage estimation technique, such as Generalized Advantage Estimation (GAE) [3].
Intuitively, this formulation looks quite similar to the update rule for the VPG algorithm (copied above for reference) with a few important differences:
The terms in the expectation are modified slightly to express the probability of a given action
aas a ratio between old and updated policies.The update has an added constraint based on the KL divergence between old and updated policies.
Instead of performing gradient ascent, we are solving a constrained maximization problem to generate each new policy5.
How do we compute TRPO’s update in practice? Well, working with the analytical update rule shown above is difficult. But—like many techniques in AI/ML—we can find an approximation to this equation that works quite well and can be computed efficiently! The details of computing this approximation are beyond the scope of this post. However, the high-level steps we take in this process are:
Approximate the objective (and constraint) with a Taylor expansion.
Solve this approximate objective function (using ideas from optimization research like Lagrangians and duality).
Use the conjugate gradient algorithm to avoid inverting large matrices when solving the problem above (this is computationally intractable otherwise!).
Perform post-processing to ensure that the updated policy both satisfies the KL divergence constraint and results in an improvement to the objective.
For more details on his this update rule is derived, check out the article below.
Using TRPO in practice. The implementation of TRPO is similar to that of VPG. We allow our current policy to interact with the environment and collect data6. From this observed data, we can compute the approximate update for TRPO as described above. Then, we can continue the process of collecting data and performing an update until we arrive at a policy that performs quite well. Because we are using the actual policy being trained to collect the data used to train it, TRPO is an on-policy reinforcement learning algorithm.
KL Divergence Constraint. Before moving on, let’s briefly consider the KL divergence constraint used by TRPO to better understand its role in the learning process. As mentioned previously, the VPG algorithm is based upon gradient ascent, which—by nature—ensures that updates to the policy’s parameters θ are not too large. In particular, we use a learning rate to perform updates with VPG, which can control the size of the update in the parameter space; see below.
Here, only the size of the update to θ is controlled—the old and updated policies are close in the parameter space. Despite this fact, small tweaks to the parameters θ may completely change the underlying policy! Even a relatively small update can drastically change the policy’s performance (or even lead to collapse). Because small changes to θ can drastically alter the policy, ensuring that policy updates are small in the parameter space does not provide much of a guarantee on changes to the resulting policy. As a result, we are constrained to relatively small updates within the VPG algorithm—larger or multiple updates could be harmful.
TRPO sidesteps this issue by considering the size of our policy update from an alternative viewpoint. Namely, we compare updated and old policies using the KL divergence, which measures the difference in probability distributions over the action space produced by the two policies. Such an approach compares policies based upon the actions they take rather than their underlying parameters θ. In this way, we can perform large policy updates while ensuring that the new policy does not produce actions that are significantly different from the old policy. Such an approach allows us to drastically speed up the learning process as shown in the figure above (single path and vine are both based upon TRPO).
Proximal Policy Optimization (PPO) [2]
“We [introduce] proximal policy optimization, a family of policy optimization methods that use multiple epochs of stochastic gradient ascent to perform each policy update. These methods have the stability and reliability of trust-region methods but are much simpler to implement … applicable in more general settings, and have better overall performance.”- from [2]
TRPO has improved data efficiency, stability, and reliability compared to the VPG algorithm, but there are still limitations that need to be addressed. Namely, the algorithm is complicated, can only perform a single update each time new data is sampled from the environment, and is only applicable to certain problem setups7. Aiming to develop a better approach, authors in [2] propose Proximal Policy Optimization (PPO), another policy gradient algorithm that alternates between collecting data from the environment and performing several epochs of training over this sampled data. PPO shares the reliability of TRPO and is i) much simpler, ii) more data efficient, and iii) more generally applicable.
Reformulating the TRPO update rule. Recall that, during each policy update, TRPO maximizes a surrogate objective to get the new policy. The surrogate objective being solved by TRPO can be reformulated as shown above. Here, we simplify our original expectation over actions/states sampled from a policy with the subscript t, which represents time steps along different trajectories sampled from the environment. This objective has two terms: the probability ratio and the advantage function. The expression for the probability ratio is shown below.
If we were to maximize this objective without any constraints, it would lead to a policy update that is too large (and potentially destructive)—this is why we leverage the KL divergence constraint. Put simply, adding a constraint to the policy update penalizes policy updates that move the probability ratio too far away from 1.
PPO surrogate objective. Similar to TRPO, we perform policy updates in PPO according to a surrogate objective. However, this surrogate objective has a “clipped” probability ratio, as shown in the equation below.
The surrogate objective for PPO is expressed as a minimum of two values. The first value is the same surrogate objective from TRPO, while the second value is a “clipped” version of this objective that lies within a certain range. In practice, this expression is formulated such that there is no reward for moving the probability ratio beyond the interval [1 - ϵ, 1 + ϵ]; see below.
In other words, PPO has no incentive for excessively large policy updates. Plus, by taking the minimum of the clipped and unclipped version of the surrogate objective, we only ignore excessive changes to the probability ratio if they improve the underlying objective. In the figure above, we see a basic depiction of this trend for both positive and negative values of the advantage function.
To understand PPO’s surrogate objective more intuitively, we should look at the figure below, which plots several objective functions as we interpolate between an old and updated policy obtained via PPO. In this figure, we see the KL divergence, the TRPO surrogate objective (labeled as CPI), the clipped surrogate objective, and the full PPO surrogate objective. From these plots, we can see that the PPO surrogate objective is a pessimistic/lower bound for the TRPO surrogate objective, where a penalty is incurred for having too large of a policy update.
While TRPO sets a hard constraint to avoid policy updates that are too large, PPO simply formulates the surrogate objective such that a penalty is incurred if the KL divergence is too large. Such an approach is much simpler, as we no longer have to solve a difficult, constrained optimization problem. Rather, we can compute PPO’s surrogate loss with only minor tweaks to the VPG algorithm.
The PPO algorithm and its benefits. So, how do we use this surrogate objective to train a neural network? PPO operates similarly to VPG and TRPO by alternating between collecting data from the environment and updating the underlying policy (i.e., it is an on-policy RL algorithm). If we are using a package like PyTorch that supports automatic differentiation, we can perform a policy update by simply constructing a loss function corresponding to the surrogate objective outlined above8 and performing several iterations/epochs of stochastic gradient ascent using this loss and samples from the observed data; see below.
PPO has several benefits compared to TRPO. First, the implementation of PPO is much simpler compared to TRPO, as we can use automatic differentiation and gradient-based optimization techniques9 instead of deriving an (approximate) solution for a complex, constrained objective function. Additionally, while TRPO makes only a single policy update each time new data is collected, PPO performs multiple epochs of optimization via stochastic gradient ascent over the surrogate objective, which improves data efficiency. See the link below for an accessible and well-documented implementation of PPO.
Finally, computing estimates of the advantage function (e.g., via GAE) typically requires that we learn a corresponding value function. In TRPO, we must learn this state-value function with a separate neural network. However, PPO—due to its compatibility with a wider scope of architectures (including those with parameter sharing)—can train a joint network for policy and value functions by just adding an extra term to the loss function that computes the mean-squared error (MSE) between estimated and actual value function values; see below.
Does it perform well? When PPO is compared to a variety of state-of-the-art RL algorithms on problems with continuous action spaces, we see that it tends to learn faster and outperforms prior techniques on nearly all tasks; see below.
In the Atari domain, PPO is found to perform comparably to algorithms like A2C [4] and ACER [5], despite these algorithms being tuned extensively for this domain. The table below outlines the number of games won by each algorithm.
The Role of PPO in RLHF
Although PPO was a useful advancement in mainstream RL research, this algorithm also had a massive impact on the space of language modeling. More specifically, InstructGPT [6]—the predecessor to ChatGPT—was aligned (i.e., trained to produce output that aligns with human expectations) via a three-part framework (shown above) that includes both supervised fine-tuning (SFT) and reinforcement learning from human feedback (RLHF). Although such an approach was explored previously for text summarization tasks [7], InstructGPT popularized this framework for training language foundation models, leading to its use in the creation of a variety of popular language models; e.g., ChatGPT, GPT-4, LLaMA-2, and Sparrow.
How does this relate to PPO? Due to its ease of use, PPO was the RL algorithm that was originally selected for use in RLHF by InstructGPT. The alignment strategy used by InstructGPT later became standardized and, though alternatives have been explored, PPO remains a popular choice for RLHF even today. As such, PPO is a pivotal aspect of language model alignment, and any AI practitioner with an interest in understanding or implementing the alignment process would benefit from a working understanding of PPO.
Takeaways
Within this overview, we expanded our understanding of basic policy gradient algorithms, such as VPG, to include more recent RL algorithms like TRPO and PPO. Compared to prior algorithms, TRPO and PPO have improved data efficiency and better reliability/stability. Notably, PPO is the primary RL algorithm used by RLHF, making it a key component of the language model alignment process. Although many factors led to the use of PPO in this domain, PPO’s ease-of-use is undoubtedly a key aspect of its success. In particular, PPO inherits the data efficiency and reliability of TRPO with several added benefits:
Improved robustness (i.e., not much tuning required)
Better data efficiency
Simplicity (i.e., only requires small tweaks to VPG)
More general (i.e., applies to a wider class of model architectures)
Due to these (many) factors, PPO is a popular choice of RL algorithm among practitioners. As the learning algorithm used for RLHF, PPO is the foundation of language model alignment. With a deeper understanding of this algorithm, we can gain a new level of insight into how language models learn and behave.
New to the newsletter?
Hi! I’m Cameron R. Wolfe, deep learning Ph.D. and Director of AI at Rebuy. This is the Deep (Learning) Focus newsletter, where I help readers understand AI research via overviews of relevant topics from the ground up. If you like the newsletter, please subscribe, share it, or follow me on Medium, X, and LinkedIn!
Bibliography
[1] J. Schulman, S. Levine, P. Moritz, M. I. Jordan, and P. Abbeel. “Trust region policy optimization”. In: CoRR, abs/1502.05477 (2015).
[2] Schulman, John, et al. "Proximal policy optimization algorithms." arXiv preprint arXiv:1707.06347 (2017).
[3] Schulman, John, et al. "High-dimensional continuous control using generalized advantage estimation." arXiv preprint arXiv:1506.02438 (2015).
[4] V. Mnih, et al. “Asynchronous methods for deep reinforcement learning”. In: arXiv preprint arXiv:1602.01783 (2016).
[5] Z. Wang et al. “Sample Efficient Actor-Critic with Experience Replay”. In: arXiv preprint arXiv:1611.01224 (2016).
[6] Ouyang, Long, et al. "Training language models to follow instructions with human feedback." Advances in Neural Information Processing Systems 35 (2022): 27730-27744.
[7] Stiennon, Nisan, et al. "Learning to summarize with human feedback." Advances in Neural Information Processing Systems 33 (2020): 3008-3021.
[8] Touvron, Hugo, et al. "Llama 2: Open foundation and fine-tuned chat models." arXiv preprint arXiv:2307.09288 (2023).
[9] Achiam, Josh. Spinning Up in Deep RL. OpenAI, 2018: https://spinningup.openai.com/en/latest/index.html
[10] Schulman, John. Optimizing expectations: From deep reinforcement learning to stochastic computation graphs. Diss. UC Berkeley, 2016.
[11] Glaese, Amelia, et al. "Improving alignment of dialogue agents via targeted human judgements." arXiv preprint arXiv:2209.14375 (2022).
Despite this fact, many open-source LLMs are aligned using solely SFT instead of a combination of SFT and RLHF. LLaMA-2 breaks this trends by heavily investing into curating a massive human preference dataset for alignment via RLHF.
By continuous domain, we mean that actions outputted by the agent are continuous, rather than discrete. For example, driving a car is a continuous domain, as we can adjust the steering wheel and pedals according to a continuous output (i.e., angle or pressure). In contrast, chess would be a discrete domain, as there are a fixed number of actions capable of being taken at each state.
We can also use other algorithms, but PPO is the original (and most common) choice of RL algorithm for RLHF. Recent research has begun to explore alternative choices.
Language models have a discrete action space comprised of all tokens that can be outputted by the model. However, this action space is still quite large. Most language models have a vocabulary size of tens to hundreds of thousands of tokens!
In discussions of TRPO, we will see this referred to as solving the “surrogate” objective. This surrogate objective simply refers to the maximization problem that we solve during each update step of TRPO. More generally, surrogate functions refer to functions that approximate other functions. In TRPO, the surrogate objective is a problem that we solve in pursuit of achieving an optimal policy!
This process is often referred to as experience replay and the data that we collect from this process is stored within a replay buffer.
Notably, TRPO cannot be used for neural network architectures that include noise (e.g., dropout) or perform any form of parameter sharing (e.g., between the policy and the value function).
The objective that we use in practice is different from what we see in the equations. This is because we cannot compute an expectation exactly, as this would require taking an average over all possible trajectories from our current policy. Instead, we collect data from the environment and take a sample mean to approximate this objective.
These are the same exact tools that we use for training neural networks according to common objectives such as supervised of self-supervised learning!








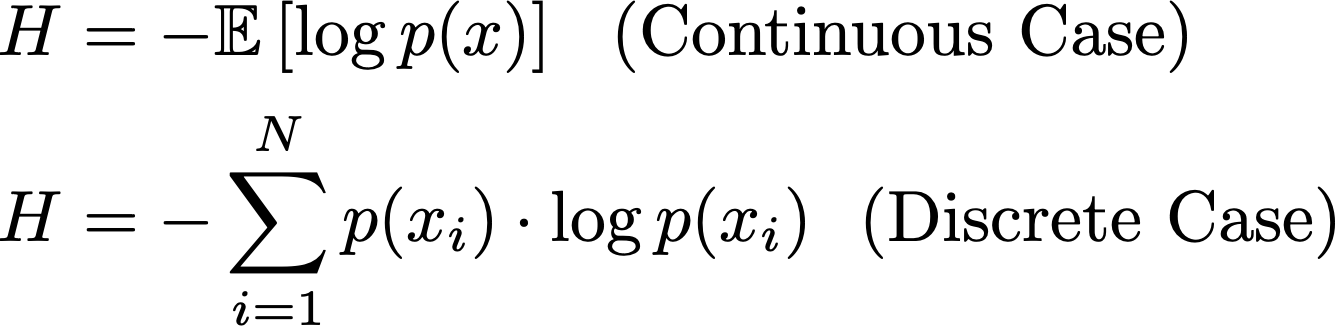
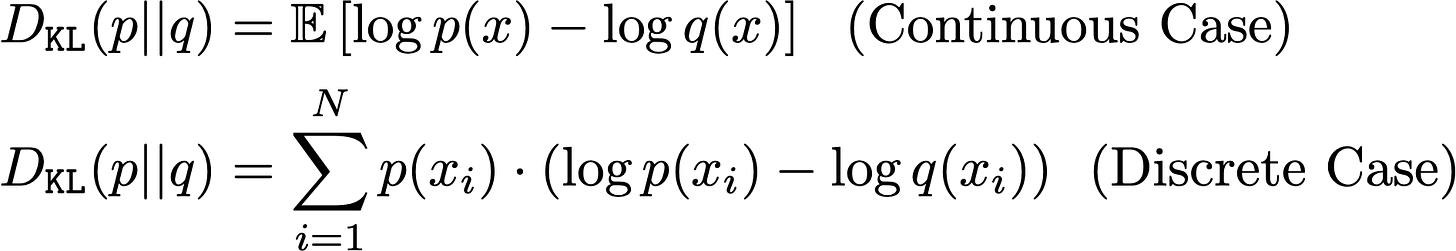













Cameron, could you recommend a SOTA textbook aimed at a graduate level audience on this topic? I know it is a dynamic area and a moving target, but a foundational text would be great.