Understanding Compositional Pattern Producing Networks
A comprehensive explanation of the theory behind CPPNS
For the last two years, I have been researching Compositional Pattern Producing Networks (CPPN), a type of augmenting topology neural network proposed in [1]. However, throughout my research, I was always baffled by some of the concepts and theory behind CPPNs, and I struggled to understand how they work. Although a few open source versions of CPPN exist online, I wanted to build my own implementation for customization purposes in my research, which turned out to be significantly more involved than I initially expected. So, I wanted to create a comprehensive explanation of the theory behind CPPNs and how they can be implemented, so that such a resource is available to everyone that struggles with CPPN just as I did. This article will be broken up into two separate parts. Part one, which you are reading right now, will focus on the theory behind CPPNs and how they have been used in scientific research, while part two will focus on actually implementing a CPPN in Python.
What the heck is this? Theory of CPPNs
Proposed in [1], CPPNs are an extension upon a previous proposed neural network, called NEAT [2]. These types of neural networks are very similar, so I am going to outline some theory behind NEAT and then quickly address the ways in which CPPNs are different (don’t worry, they are nearly identical). First of all, NEAT is an augmenting topology neural network that is evolved with a genetic algorithm. The explanation for what this means can be broken into two related ideas: evolutionary/genetic algorithms and augmenting topology networks.
Genetic Algorithms
Evolutionary/Genetic algorithms (GA) are used to train and optimize the parameters of a neural network, similar to back propagation or hill climbing. However, instead of using derivatives to always tweak a network’s weights in the direction that improves loss, GA finds optimal sets of weights through a computer’s version of natural selection, drawing inspiration from Darwinism and survival of the fittest. By creating a huge “population” of possible weight matrices (usually ~25–100, but this can vary), GA can assess the loss for each of these “individuals” within the population, each represented by a unique weight matrix. Using this information, the best weight matrices are then mutated, crossed over with each other, and selected to advance to the next “generation”. By repeating this process over many generations, or iterations of the selection process, GA can create a final population of weight matrices that minimize loss, thus yielding many possible weight matrices that perform optimally.
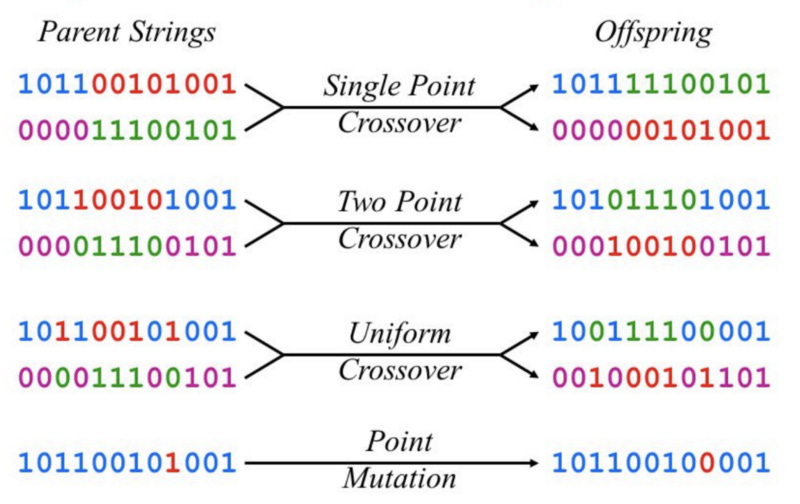
Mutation is performed by randomly perturbing the weights of a single network, while crossovers are performed by partially swapping the weights of one network with those of another. These concepts were always a bit confusing to me, so here is a visual representation of two sets of weights being crossed over and mutated:
In the above figure, it can be seen that, during crossover, a large portion of the weights are swapped between the weight matrices, thus yielding two “child” weight sets that are different than the original “parents”. During mutation, some weights are perturbed in a random direction to make the “child” set of weights slightly different than the original.
This process of mutating, crossing over, and selecting the best weight matrices for survival is repeated for many generations until you are left with a final population of optimal weight matrices. With this methodology, only the best solutions advance to successive generations to be further mutated, crossed over, and explored. Therefore, over time, the population is optimized using the Darwinian principle of survival of the fittest. If you are curious and would like to learn more about GA, I encourage you to check out this link, which is a lot more in depth than the explanation I gave here.
Augmenting Topology Neural Networks
Normally, GA works on a set of networks that all have the same structure. Augmenting topology neural networks also utilize GA, but they allow GA to manipulate the structure of neural networks during evolution (not just the weights), thus allowing the optimal structures/topologies for neural networks to be found. At the beginning of evolution, all neural networks are initialized with inputs fully connected to outputs and no hidden nodes — a very simple, minimal structure. However, with augmenting topology, as the weights of the neural network are “evolved”, the structures of networks are being simultaneously optimized — this does not occur in typical GA optimization. To explore possible network topologies, the GA, when augmenting topologies are allowed, adds complexity into networks by adding hidden nodes, adding more connections, and even deleting existing connections within certain topologies in the population. Therefore, although the networks are structurally simple at the beginning of evolution, their topologies are evolved to yield higher performance, thus allowing training to create more complex network structures. This concept of augmenting topology is the core idea behind NEAT/CPPN and, in my opinion, is what makes the models so powerful. The below figure gives a visual representation of how topology mutations are applied to networks throughout evolution:
In the above figure, an existing connecting was split into two new connections, and a node was added in between the two connections. In addition to this type of topology mutation (called a node mutation), NEAT also has topology mutations that add connections into the network (connection addition mutation) and others that remove connections from the network (connection deletion mutation). Such topology augmentations result in a final population of networks that are quite diverse in their structure but all accomplish a similar task — each network within the population may have a different topology that solves the problem differently.
Difference between CPPN and NEAT?
Now that you have a high level understanding of NEAT, you are probably curious why I am writing about a completely different type of network than the one mentioned in the title (CPPN), but the difference between the two is quite simple. Instead of using the same activation function within every node, CPPN allows each node to contain a unique activation function selected from a list of possible activations functions. This list of activations may include sin, cos, tanh, sigmoid, relu, or any other activation function you might want to include. Allowing the neural network to contain many different activation functions, in turn, allows it to model functions that exhibit properties of all these different activations and create output that is patterned, symmetrical and unique. The purpose of the CPPN then, because of its ability to create such complex and interesting geometries, is to generate 2D and 3D shapes of various kinds. The inputs into the CPPN are the x and y (and possibly even z) locations of a pixel, and it outputs a value for the pixel (between [0, 1] or [white, black]) at that inputted location. This activation is repeated for every possible pixel location within a 2D or 3D space to yield a full output shape. The typical activation of a CPPN can be visualized with the following figure:
In this image, it can be observed that the x and y locations of a pixel are inputted into the CPPN and a value for the intensity of the pixel at that x and y location is outputted. Each node within the CPPN contains a unique activation function that impacts the value of the output in different ways depending on the inputted values. By performing this activation of the CPPN for every pixel location within a 2D or 3D space, one can create interesting structures and patterns such as those shown here:
As can be observed in the above outputs, the ability of CPPN to produce regular and symmetrical shapes is well suited to evolving structures that resemble artwork, living organisms, and many other interesting geometries. Such an application and capability, in my opinion, is quite interesting and why I found studying CPPNs to be so intriguing.
Details of Evolving CPPNs
At the beginning of evolution, the population of CPPNS is initialized with simple structures containing no hidden nodes, but, due to the augmenting topology feature of CPPNs, the population becomes increasingly more complex as evolution continues and topological mutations are applied. Extra nodes and connections are added into network structures during each generation, thus yielding networks that are increasingly complex and more suited to solve the desired problem. However, it is very important to realize that all networks within the population are not mutated simultaneously and, therefore, each network may have a different topological structure than other CPPNs within the population. Such lack of uniformity between network topologies makes evolution of CPPNs somewhat unique and difficult, so I thought it would be worthwhile to explain some of the details of how CPPNs are typically evolved and how such lack of structural uniformity is handled.
Historical Markings
Each time a new connection is added into a CPPN’s topology, it is given a “historical marking” or “innovation number”, which is simply an integer unique to that specific connection. Each connection added to every CPPN within the population is given a unique historical marking. As connections are added throughout evolution, a global counter is maintained and incremented so that every historical marking assigned is unique. Such historical markings allow one to understand the history and lineage of each connection within the population. Additionally, as structures are crossed over with each other throughout evolution, one can observe which connections are of similar evolutionary descent using historical markings. By performing such simple book-keeping on added connections, several aspects of evolving CPPNs are greatly simplified. In the figure below, you can observe a list of connections and their corresponding innovation numbers (innovation numbers and historical markings are the same thing!).
Notice that each connection in the image above is assigned an innovation number and the innovation number of every connection is unique. This allows you determine which networks within a population share common connections and, in turn, are descended from the same structures.
Crossover of CPPNs
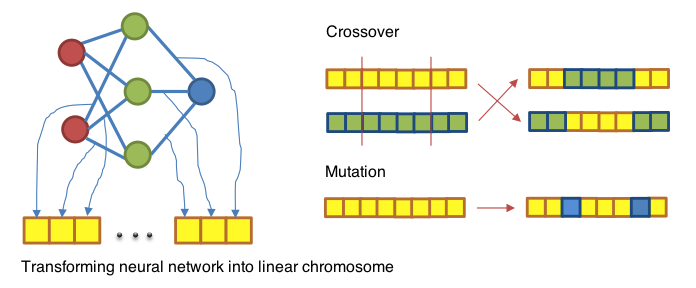
As mentioned previously, part of evolving neural networks with GA involves crossover — the swapping of weight values between networks to create new networks. For the typical evolution of neural networks with GA, crossover is quite simple. Here is a figure to visualize common types of crossover between same-topology networks:
For the evolution of augmenting topology CPPNs, crossover becomes slightly more complicated due to the fact that the number of weights between two networks may not be the same. However, the process is greatly simplified with the use of innovation numbers. Instead of trying to find a special way to decide which weights to crossover with each other, only weights with the same innovation numbers are crossed over. Therefore, crossover can be performed simply by finding connections with equal innovation numbers between the two networks and swapping their weights, thus yielding a pseudo-uniform crossover between CPPNs.
Preserving Diversity through Speciation
As topology mutations (new connections and nodes) are added to the topology of CPPNs within a population, such mutations usually cause an initial decrease in fitness. This decrease in fitness is caused by the fact that new weights placed into the network are random when initialized and, although topology changes may provide a more optimal structure, such weights must be trained before the network realizes its full potential. Such new, random weights within the network generally cause the fitness of a network to fall initially, then improve once the weights are trained. If we did not protect such networks from selection, allowing them time to train and realize their maximum fitness, they would be weeded out of the population immediately by the GA, which would prevent CPPNs from exploring more complex structures. Luckily, such new structures can be preserved through an important concept, called “speciation”.
Personally, speciation was the most difficult concept for me to understand while studying CPPNs, but CPPNs cannot be evolved effectively without it. The basic concept behind how speciation works is that CPPNs, when being selected for the next generation, should only compete with CPPNs that have similar topologies. That way, if a network with a new, more complex topology is created through mutation, it will not have to compete with less complex topologies that have already reached their maximum fitness, thus giving the more complex network time to train and improve its fitness. The similarity of topologies is assessed by comparing innovation numbers between networks — if networks have a lot of connections with the same innovation numbers they are more similar and vic versa. Using such information, when selection is performed, CPPNs are separated into several “species”, or distinct groups with similar topologies, based on the innovation number distance metric. Once these species have been formed, selection is performed separately for each species, allowing CPPNs to only compete with other members of their species. This method allows CPPNs with new, distinct structures to survive long enough for training and optimization to discover if such a topology is optimal.
CPPN Evolution Summary
If you understand all of these special details for evolving CPPNs, you have a pretty good understanding of the theory behind CPPNs and could probably understand most of the papers and projects published using CPPNs. I believe that this figure summarizes a lot of these details very nicely:
As seen in the above figure, the population of CPPNs to be evolved starts minimally — fully-connected with no hidden nodes in any of the structures. As evolution proceeds, topological and weight mutations are applied to CPPNs, which allow them to grow, become more complex in structure, and optimize their parameters. As new connections are added to CPPNs, they are each given a unique historical marking (or innovation number) that allow similar connections to be identified. These historical markings can then be used to create a distance/similarity metric between different network topologies, which allows CPPNs to be separated into different species based on their network structure. By performing selection separately on each species, new CPPN topologies are allowed to survive selection and evolution long enough for their capabilities to be explored, thus allowing the best network structure to be found and optimized.
Example Projects/Studies Involving CPPN
Now that you understand how CPPNs work and the cool stuff they can do, it would probably be helpful to look at some research projects that have been done with CPPNs, some of which have been quite impactful in the field of computational evolution.
Picbreeder Website
One of the initial issues faced in researching CPPNs was the fact that, in many cases, the fitness of a certain network is difficult to determine. Each CPPN outputs a unique shape or image, and assigning a fitness to such an output is quite subjective — the user must determine the fitness based on their preferences. Picbreeder.com is a website that was developed as a research project to crowd-source the evolution of CPPNs on a large scale, completely based on user preference. Using CPPNs to encode many different images, the website allows users to select images that they enjoy and evolve them by continually selecting mutated versions of the image for further evolution. Evolution could even be later continued on the same image by a different user. Such a platform allowed CPPNs to be evolved for an incredible number of generations, completely based on subjective user input, which led to the collective creation of a diverse set of interesting outputs. Here are a few of the examples of some images that were evolved on the website:
As can be seen above, some pretty interesting and impressive images were created through such collaborative evolution. Additionally, the results of evolution in this study effectively demonstrated many valuable properties of CPPNs that make them useful and interesting. For example, consider the following set of images that were also evolved using picbreeder:
From the above images, it becomes quite clear that CPPNs can produce symmetrical and regular geometries that resemble living organisms, which is one of the primary motivations behind their creation. Therefore, the results of evolution on picbreeder.com solidify the effectiveness of CPPNs in achieving this purpose.
Soft Robot Evolution
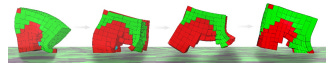
Many papers have been published exploring 2D applications of CPPNs with images, but I have found that many of the most interesting applications involve the production of 3D shapes. One of the most prominent 3D applications of CPPNs studied the evolution of soft robots that were indirectly encoded by CPPNs to achieve maximum distance traveled. Right now, you are probably thinking “wait … what the heck is a soft robot,” so here is a quick picture of what the soft robots in this paper looked like:
In this study, soft robots were created by adding material into a 3D space that can be expanded and contracted in different ways (hence “soft” robots), which causes the robot to move like a living organism. These soft robots were created by filling a 3D space with voxels (3D pixels) of different types (or no voxels/empty space) to create a structure. Each type of voxel (represented by the different colors) contracts or relaxes differently so that, when paired together, the movement of the voxels can create overall motion of the structure. Such structures were created by querying a CPPN at each possible voxel location in the output space to yield an output for the type and presence of each voxel. In this study, the model also used distance from the center of the space (d) as an input, but I have found that normalizing the position input values reduces the number of parameters within the network and performs similarly. Here is a visualization of how the CPPNs were used to create soft robot outputs in this project if you are still a bit confused:
Each structure was evaluated by a simulation that determined the distance each soft robot moved in a given time. The study was successful in evolving CPPNs that were able to move maximum distances and, interestingly enough, many of these evolved structures resembled living organisms in their locomotion (check out this video if you’re intrigued!). Furthermore, when this problem was attempted using only a direct encoding of the soft robot (storing values for every voxel in the structure directly) and evolved with GA, it did not work at all, thus demonstrating the usefulness and effectiveness of CPPNs in creating lifelike, functional creatures. Here are images of some of the best soft robots that were evolved in this study:
Other Papers/Studies
There are a lot of papers that have explored the effectiveness and capabilities of CPPNs, but writing about them all would take forever (and I’m sure you’re tired of reading at this point). So, here is a list of a few extra papers that I have found useful and interesting regarding CPPNs throughout my research:
The Emergence of Canalization and Evolvability in an Open-Ended, Interactive Evolutionary System
Evolving Three-Dimensional Objects with a Generative Encoding Inspired by Developmental Biology
Conclusion
Thanks so much for reading! I hope you now have a better understanding of CPPNs and how they can be used. If you are curious and want to learn more about CPPNs, I really encourage you to visit the webpage for NEAT, which was started by the creator of NEAT to allow researchers to share ideas and methods regarding NEAT (remember, NEAT is almost identical to CPPN so most ideas/tips apply to both!). Additionally, feel free to reach out to me on LinkedIn or follow me on GitHub.
Citations
[1] K. O. Stanley. Compositional pattern producing networks: A novel abstraction of development. Genetic Programming and Evolvable Machines, 2007.
[2] K. O. Stanley and R. Miikkulainen. Evolving neural networks through augmenting topologies. Evolutionary Computation, 2002.
[3] Cheney, N., MacCurdy, R., Clune, J. and Lipson, H. Unshackling evolution: Evolving soft robots with multiple materials and a powerful generative encoding. In Proceedings of the Genetic and Evolutionary Computation Conference. ACM, NY, 2013.