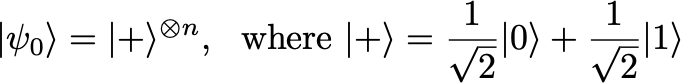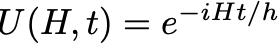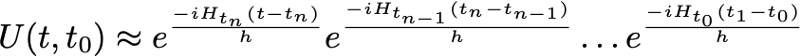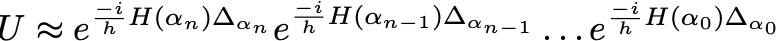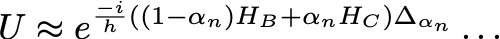The Quantum Approximate Optimization Algorithm from the Ground Up
Understanding QAOA, its motivation, and how it was derived from past algorithms in the quantum computing community.
Introduction
In recent years, the advent of quantum computing has brought great excitement within numerous research communities (e.g., physics, computer science, mathematics, etc.). Interest in the topic of quantum computing led to numerous theoretical contributions in the space, catalyzing the development of influential algorithms such as Grover’s search, Shor’s algorithm, adiabatic optimization, and many more. Despite these theoretical demonstrations of quantum supremacy and usefulness, such algorithms go beyond the current reality of quantum hardware, utilizing an excessive circuit depth and number of qubits. As of now, such requirements are unrealizable within a physical system.
Currently, quantum computing is said to exist within the Noisy Intermediate-Scale Quantum (NISQ) era, in which hardware is limited in the number of available qubits and circuit depth is limited by increasing noise that arises within a quantum system. As such, many of the most eminent quantum algorithms (such as those mentioned above) have limited practical applications, leading researchers to focus on the development of NISQ-friendly quantum algorithms. Two of the most widely-studied algorithms in this space are the variational quantum eigensolver (VQE) and the quantum approximate optimization algorithm (QAOA), which are both variational quantum algorithms (VQA) that use parametric quantum circuits (with parameters optimized classically) to optimize functions (e.g., minimum eigenvalue/eigenvector pair, maximum cut on a graph, maximum vertex cover on a graph, etc.). In this post, I aim to explain QAOA in depth, assuming only a mild background understanding of quantum computing (i.e., qubits, quantum states, and basic linear algebra); see this blog post if you are interested to learn more about VQE.
I will begin by explaining QAOA at a high level, including the components of the algorithm and how it can be used to solve problems of interest. Following an initial description of QAOA, I will overview numerous concepts in quantum mechanics and mathematics that are relevant to developing an in-depth understanding of QAOA. Once such background is clear, I will explain the details of the adiabatic algorithm for quantum computing, which is intricately related to QAOA, in an attempt to understand how QAOA is related to the algorithms that preceded it. At the end of the post, I will return to a discussion of QAOA, aiming to motivate the components of the algorithm by drawing connections to the adiabatic algorithm for quantum computing.
The Quantum Approximate Optimization Algorithm
QAOA is a variational quantum algorithm (i.e., a hybrid quantum-classical algorithm involving parametric quantum circuits that are classically optimized) that was proposed for finding approximate solutions to combinatorial optimization problems (e.g., MaxCut, Maximum Vertex Cover, MaxSAT, etc.). At a high level, QAOA applies a series of parametric quantum gates to some initial state, and optimizes the parameters of these gates such that the final state (after the quantum gates have been applied) encodes an approximate solution to some problem of interest (i.e., if you take a measurement of the final state with respect to the computational basis it will produce a high-quality solution). The QAOA framework involves several components. Here, I simply define the relevant components and illustrate how they are combined together without deeply considering their motivation, thus providing a basic understanding of QAOA as a whole.
Cost and Mixer Hamiltonians
Assume we are studying a quantum system with n total qubits. Within QAOA, there are two Hamiltonians of interest — the mixer Hamiltonian and the cost Hamiltonian. Each of these Hamiltonians are complex-valued matrices of dimension 2^n x 2^n. But, to understand their purpose, we must first understand the role of a Hamiltonian in a quantum system. In quantum mechanics, a Hamiltonian is a hermitian matrix that encodes the energy of a quantum system. In particular, the eigenvalues of the Hamiltonian, which are real-valued because the matrix is hermitian, represent the possible energy levels of the system (i.e., the set of possible outcomes when measuring the system’s total energy).
A common pattern within quantum algorithms is to encode a problem of interest (e.g., minimization/maximization of some function) within a Hamiltonian matrix and find a way to generate a quantum state that, when measured with respect to that Hamiltonian, produces the lowest/highest possible energy. Within QAOA, the cost Hamiltonian, which we will denote as H_C is constructed in this way, encoding the solution to some problem of interest (e.g., a MaxCut or MaxSAT instance) within its lowest energy state. For QAOA, the cost Hamiltonian is typically constructed using Ising models, which can be used to encode combinatorial optimization problems as Hamiltonians with single-qubit Pauli-Z terms. Although we will not detail the construction of cost Hamiltonians with Ising models in this post, this paper covers the topic pretty extensively. Unlike the cost Hamiltonian, the mixer Hamiltonian is unrelated to the problem definition and is defined as follows.
In the equation above, all sigma variables correspond to single qubit Pauli-X matrices on the i-th qubit. One important property of the mixer Hamiltonian is that it should not commute with the cost hamiltonian. If these matrices do not commute, then they cannot share any eigenvectors, which prevents the QAOA ansatz (see below) from getting stuck in non-optimal states with higher energy.
Initial State
From here, we must also define the initial quantum state used within QAOA, which is given below.
Here, z is used to denote the computational basis for our quantum system. This initial state may also be written as follows (i.e., the two definitions are identical).
As can be seen above, the initial state within QAOA is simply a product of maximally-superposed states across each qubit. Interestingly, this initial state is the maximum eigenvector of the mixer Hamiltonian — it will become clear why this is important later in the post. Additionally, this state is extremely easy to construct — just apply a Hadamard gate separately to each qubit within the system — which makes it a desirable choice if QAOA should be implemented on actual quantum hardware.
QAOA Ansatz
Now, we have defined all relevant components of QAOA, but it is unclear how these components can be combined together to solve an optimization problem. As previously mentioned, QAOA evolves the initial state using a series of parametric quantum gates, where each quantum gate is described as multiplication of the quantum state by a unitary matrix. Quantum gates are always unitary to ensure that evolution of the quantum state is adiabatic and that the normalization property of the quantum state is preserved. The evolution of the initial state in QAOA is described by the following ansatz, which produces a final state that (hopefully) encodes an approximately optimal solution to the problem of interest.
Here, beta and gamma are real-valued, scalar parameters. The QAOA ansatz, containing 2p parameters in total, is comprised of a series of alternating unitary gates with different scalar parameters. As can be seen, the “depth” of this ansatz is p, as the alternating gate structure is applied to the initial state p times consecutively. The unitary matrices that evolve the intial state are constructed by taking matrix exponentials of the cost and mixer Hamiltonians (i.e., the exponential of a hermitian matrix is always unitary). Therefore, QAOA, using the above ansatz, produces a new quantum state by applying a series of parametric unitary gates, based on the cost and mixer hamiltonians, to an initial state. If we want this final state to encode a solution to our problem of interest, all we have to do is set beta and gamma parameters such that the output of QAOA is a low energy state of the cost Hamiltonian. But… how do we find the correct parameters?
Optimizing QAOA Parameters
The expected energy of our final state with respect to the cost Hamiltonian can be expressed as follows, where Tr() denotes the trace of a matrix.
This expected value can be computed in practice by taking repeated, identical measurements of the state produced by the QAOA ansatz. Then, using a classical computer, the gradient of this function can be computed (e.g., using the parameter shift rule), allowing the beta and gamma parameters to be updated in the direction that mimizes the expectation with respect to the cost Hamiltonian. By iteratively repeating this process, the parameters of the QAOA ansatz are updated such that the energy of the final state is minimized. As a result, an approximately optimal solution can be generated by producing this final state and taking a measurement with respect to the computational basis (i.e., this can be done multiple times to ensure a good solution is found, due to the fact that measurements in quantum systems are stochastic). Note that the solution provided by QAOA is approximate, and not guaranteed to be globally optimal.
Background Information for Understanding QAOA
Now, we understand what QAOA is, but the motivation behind its components is unclear. If you are like me, the constructions within QAOA may seem arbitrary, leaving you wondering why it works and how someone even devised such an algorithm. In order to clarify some of this confusion, there is some background information that must be understood, which I aim to outline in this section.
Matrix Exponentials
Although matrix exponentials were briefly outlined in the description of QAOA, it is worthwhile to futher outline some of their major properties, due to their relevance to the QAOA ansatz. As stated before, the exponential of a Hermitian matrix is always unitary. In fact, any unitary matrix can be written in the following form.
where H is an arbitrary hermitian matrix, i is the imaginary unit, and gamma is an arbitrary scalar parameter. Typically, quantum gates are constructed by performing time evolution of a quantum state with respect to some Hamiltonian of interest. Such time evolution takes the form of a unitary matrix as shown below, where h denotes the Planck constant.
As demonstrated by the expression above, an intricate connection exists between the evolution of a quantum state and the (exponentiated) Hamiltonian matrix. Matrix exponentials of Hamiltonians arise often as a way of performing time evolution of a quantum state within some system of interest. Additionally, the scalar parameter used within the matrix exponent can be interpreted as the total time for which such evolution is performed. In the case of QAOA, evolution occurs with respect to the cost and mixer Hamiltonians in an alternating fashion and we perform classical optimization to determine the optimal times for which each of our alternating unitary gates are applied.
Aside from their conection to the evolution of quantum state, there is one more property of matrix exponentials that will be useful. If two matrices commute with each other, then the following property of matrix exponentials is true.
This property becomes relevant when we discuss Trotterization later in the post. Additionally, based on this property, one may notice that the order of unitary matrices within the QAOA ansatz would be irrelevant if the cost and mixer Hamiltonians commute, thus providing extra reasoning regarding the requirement that the two Hamiltonians must not commute.
The Schrödinger Equation
It may seem like the above expression for time evolution with respect to some Hamiltonian came out of nowhere, but it is actually derived from the Schrödinger equation — an extremely famous partial differential equation for expressing quantum states and how they change over time. There are many ways that this equation can be written, but for the purposes of this blog post I will express it as follows.
Here, the Schrödinger equation describes the dynamics of a quantum state at time t with respect to some Hamiltonian H. Interestingly, if H is time-independent (i.e., the Hamiltonian does not change with respect to the time t), the above equation can be solved to yield the following.
As can be seen, the unitary matrix given by the Schrödinger equation to evolve the initial quantum state for time t is identical to the expression given in the previous section.
At this point, it seems like determining the dynamics of a quantum state is pretty easy — what’s the problem? Well, the problem arises when the Hamiltonian in question is not time-independent. Namely, if the Hamiltonian changes with respect to the time t the Schrödinger equation becomes extremely difficult (oftentimes impossible) to solve. So, we must find an approximation to its solution in order to evolve a quantum state with respect to a time-dependent Hamiltonian.
Approximate Evolution through Discretization in Time
So, how do we find such an approximate solution? Well, we know that the evolution of our quantum state for time t can be described by a unitary matrix. Let us denote this unitary matrix as shown below, where evolution occurs from time t0 to time t.
Often, the first step in approximating something that is continous in time (such as the unitary matrix shown above) is dividing it into discrete time steps that can be combined together. This is shown below (note that the product of two unitary matrices is always unitary).
The discretization of our unitary matrix into many, smaller timesteps is analogous to approximating a continuous function with many piecewise components. Namely, as the number of discrete timesteps increases, the approximation becomes more accurate. Going further, the unitary matrices for each discrete timestep can be expressed with respect to a time-dependent Hamiltonian, as shown below.
As can be seen above, by taking discrete steps in time, we can approximate continuous time evolution with respect to a time-dependent hamiltonian by repeatedly doing the following: (1) getting the Hamiltonian at some fixed time, (2) assuming the Hamiltonian is fixed for a short time interval, and (3) performing evolution with respect to this fixed Hamiltonian for a short time. By performing such discrete evolution over very short time periods, we create a cascade of unitary matrices that, when combined together, approximate the desired time evolution with respect to a time-dependent Hamiltonian.
Trotterization (Suzuki-Trotter Decomposition)
Discretization in time may oftentimes not be the only required component for approximating evolution with respect to a time-dependent Hamiltonian. This is because Hamiltonians are often expressed as sums of multiple, non-commuting Hamiltonians, yielding an expression resembling the one below.
In the expression above, the matrix exponential cannot be decomposed as a product of several unitary matrices because each of the Hamiltonian’s components do not commute (i.e., recall the final property from the previous explanation of matrix exponentials). As a result, we encounter the following problem.
Because implementing a quantum gate based on a sum of multiple, non-commuting Hamiltonian components is difficult, practitioners often rely upon the Suzuki-Trotter decomposition (i.e., commonly referred to as “Trotterization”) to decompose such an expression as a product of multiple unitary matrices. This decomposition has the following form.
Using the Suzuki-Trotter decomposition, the unitary introduced at the beginning of this section can be approximated by a repeating cascade of separate matrix exponentials for each of the Hamiltonian’s non-commuting components. Such a decomposition greatly simplifies the implementation of this unitary matrix as a quantum gate, which is extremely relevant for NISQ-friendly quantum algorithms such as QAOA. As a result, Trotterization arises very frequently within quantum computing.
Quantum Adiabatic Algorithm
The final step in gaining and in-depth understanding of QAOA is understanding the algorithm from which it was derived: the quantum adiabatic algorithm (QAA). QAA is an algorithm that was originally proposed for finding exact solutions to combinatorial optimization problems with the use of adiabatic evolution. At a high-level, QAA is similar to QAOA, as it begins in some initial state and evolves this state to produce the low-energy state of a cost hamiltonian. However, QAA is not an algorithm that can be implemented on NISQ devices, as it requires evolution be performed for a (potentially) very long time, exceeding the capabilities of current hardware.
Adiabatic Theorem
QAA relies upon the adiabatic theorem of quantum mechanics. Given a time-dependent Hamiltonian and a low-energy eigenstate of that Hamiltonian at time t0, the adiabatic theorem states that, if the quantum state is evolved slowly enough for time t, it will remain as the low-energy state of the Hamiltonian through time (i.e., the resulting state after evolution is the low energy state of our Hamiltonian at time t0 + t). This theorem relies on the assumption that a gap exists between the two lowest eigenvalues of the Hamiltonian at any given time. Additionally, the amount of time required for evolution is dependent upon this gap, and may become arbitrarily large if the gap is small. Furthermore, the value of this gap cannot be estimated in general, making it difficult to determine to total amount of time required to perform such an evolution.
Solving Optimization Problems with the Adiabatic Theorem
Based on the adiabatic theorem, QAA makes the following proposal. Assume that we have some combinatorial optimization problem instance that we want to solve. Remember from the previous description of QAOA that we can encode this problem instance within a cost Hamiltonian, such that the solution to the problem is given by the Hamiltonian’s low-energy state. Additionally, recall that the previously-defined mixer Hamiltonian has a low-energy state that is easy to construct (i.e., the initial state within QAOA). Then, assume we define the following time-dependent Hamiltonian, based on the cost and mixer Hamiltonians defined within the description of QAOA.
Given the above time-dependent Hamiltonian, we can easily construct the low-energy state at time 0 (i.e., it is just the low-energy state of the mixer Hamiltonian). Additionally, the time-dependent Hamiltonian at time T is equal to the cost Hamiltonian. Therefore, if we evolve this intial state for long enough, we will eventually produce the low-energy state of the cost Hamiltonian according to the adiabatic theorem (i.e., we are guaranteed a non-zero eigengap by the Perron-Frobenius theorem). As a result, such an evolution produces an exact solution to our problem of interest!
Back to QAOA
Now that we have covered relevant background information, it is time to return to QAOA and gain a more comprehensive understanding of its motivation. In particular, QAOA can be interpreted as an approximation of QAA, which can be derived by leveraging the tools we have discussed so far.
From QAA to QAOA
Both QAOA and QAA begin with the same initial state (i.e., the equal superposition state) and attempt to evolve this initial state to produce the low-energy state of the cost Hamiltonian. Consider the following time-dependent Hamiltonian, which is an interpolation between the mixer and cost Hamiltonians.
As previously outlined, expressing evolution with respect to a time-dependent Hamiltonian in closed form is very difficult. So, we must approximate this evolution using discrete time steps, as shown below. We denote the unitary that exactly expresses the evolution of our quantum state with respect to the time-dependent Hamiltonian for time t as U .
where Delta represents the length of each discrete timestep between time 0 and t. Furthermore, each time-dependent Hamiltonian term within the expression above can be expressed with respect to the cost and mixer Hamiltonians (from this point onward, only the first term in the sequence is listed to ease readability — other terms follow the same pattern).
From here, we can take the Suzuki-Trotter decomposition to arrive at the following expression, where we take p to be some large, positive integer. Recall, that the cost and mixer Hamiltonians do not commute. Thus, we are required to perform Trotterization to decompose the matrix exponential in this way.
This is starting to look somewhat familiar… By denoting the constants in front of each Hamiltonian (exluding the imaginary components) as beta and gamma , we arrive at the following expression.
So, after decomposing our evolution into discrete time steps and applying Trotterization, we arrive at an expression that (almost) exactly resembles our ansatz from QAOA! Therefore, QAOA can be motivated as an approximation of QAA in which thebeta and gamma parameters are not fixed and the depth p can be set arbitrarily! Intuitively, the quality of this approximation must improve as the depth of QAOA is increased, as the Suzuki-Trotter decomposition is only true in the limit of infinite p. Interestingly, several theoretical results for QAOA are derived by assuming an ansatz of infinite depth and drawing connections to QAA and the adiabatic theorem.
Important Distinctions
Although QAOA can be interpreted as an approximation of QAA, there are several important distinctions to be made between these algorithms. First, QAOA is a variational quantum algorithm, containing parametric quantum circuits that are classically optimized to satisfy some objective. In contrast, the corresponding “parameters” within QAA are fixed based on the time intervals used within the approximation of the unitary matrix that encodes the time-dependent evolution of the quantum state. As a result, QAOA does not necessarily approximate QAA, as its parameters can be set arbitrarily and may not reflect the discrete time interval constants that arise within QAA. Additionally, the depth of QAA may be arbitrarily large, while the depth of the QAOA ansatz is usually much smaller in order to accommodate quantum hardware limitations (i.e., the deepest QAOA ansatz that has been physically implemented has a depth of only three) — remember, QAOA is a practical algorithm for NISQ-era quantum computers. As a result, the connection between practical QAOA algorithms and QAA are, in reality, quite limited. Finally, QAOA finds an approximate solution to the problem of interest, while QAA is finds the globally optimal solution given enough time, making the goal of the two algorithms are somewhat different.
Conclusion
In this post, I tried to provide a relatively comprehensive understanding of QAOA from the ground up. By providing relevant background, I drew a connection between QAA and QAOA, revealing that QAOA can be interpretted as an approximation of QAOA (despite the practical differences that exist between the two algorithms). This sheds light on the motivation for various aspects of QAOA, such as the choice of mixer Hamiltonian (i.e., derived from QAA) and the alternating unitary structure (i.e., can be interpreted as a discrete, Trotterized approximation of QAA).
Thank you for reading, and I hope you enjoyed the post. If you find any errors or have suggestions, feel free to contact me. Furthermore, if you are interested in this topic, I would encourage you to check out my research lab at Rice University, which performs research related to numerous topics in quantum computing.