Confidence Calibration for Deep Networks: Why and How?
Making your neural network output confidence scores that actually mean something without much effort.
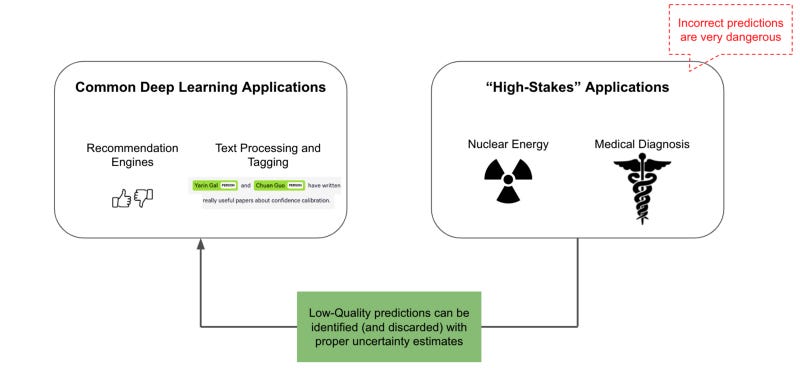
Confidence calibration is defined as the ability of some model to provide an accurate probability of correctness for any of its predictions. In other words, if a neural network predicts that some image is a cat with a confidence of 0.2, this prediction should have a 20% chance of being correct if the neural network is calibrated properly. Such calibrated confidence scores are important in various “high-stakes” applications where incorrect predictions are extremely problematic (e.g., self-driving cars, medical diagnosis, etc.), as calibrated probability scores associated with each prediction allow low-quality predictions to be identified and discarded. Thus, even if neural network output cannot yet be fully explained, confidence calibration provides a practical avenue for avoiding major mistakes in practice by associating each prediction with an accurate uncertainty/confidence score.
Within this blog post, I will explore the topic of confidence calibration within deep learning, beginning with the motivation behind confidence calibration, why it is important, and how it can be used. I will then overview common methods of measuring confidence calibration, including brier score, expected calibration error, maximum calibration error, and others. Finally, I will overview existing confidence calibration methodologies within deep learning, focusing upon the methodologies that are most effective and efficient in large-scale applications.
Why does calibration matter?
Practitioners often erroneously interpret predictive probabilities obtained from a neural network (i.e., the softmax scores) as model confidence. However, it is widely known that modern neural networks often make poor (i.e., incorrect) predictions with softmax scores of nearly 100%, making predictive probability a poor and misleading estimate of true confidence [2]. Although earlier generations of neural networks were not as “overconfident” in this way, the problem of obtaining accurate uncertainty scores from neural network predictions is non-trivial — how can we make softmax scores actually reflect the probability of correctness for a given prediction?
Currently, deep learning has been popularized in numerous fields (e.g., image/language processing) and is commonly used in applications where mistakes are acceptable. Consider, for example, an e-commerce recommendation application, where a neural network might make high-quality recommendations in 90+% of cases but fail occasionally to discover the most relevant products. Although such applications are plentiful, the deployment of deep learning into high-risk fields such as medical diagnosis or nuclear energy requires that incorrect model predictions be minimized as much as possible. As such, accurately predicting model uncertainty is an impactful problem with the potential to expand the scope of deep learning.
Potential Applications
Given that confidence calibration is a non-trivial problem with the potential for a large impact on the deep learning community, one may wonder what types of applications depend most on properly-calibrated uncertainty. Though there are many, I outline a few within this section to provide relevant context and motivate the benefit of confidence calibration in practice.
Filtering poor predictions. Given a properly-calibrated model, predictions with high uncertainty (or low confidence) can be discarded to avoid unnecessary model errors. Such an ability to discard incorrect predictions based upon a confidence score associated with each prediction is especially impactful in the high-risk applications mentioned above. Although truly explaining or understanding neural network output may remain difficult in the near term, properly calibrated uncertainty scores provide a practical avenue for detecting and avoiding a neural network’s mistakes.
Model-aware active learning. Proper uncertainty estimates enable data that is poorly-understood by the model to be easily identified. As a result, data associated with low-confidence predictions can be set aside and passed to a human annotator to be labeled and included in the model’s training set. In this way, model uncertainty can be used to iteratively identify data that the model doesn’t understand, enabling a form of model-aware active learning.
Detecting OOD data. Models with good calibration properties can often be applied to detecting out-of-distribution (OOD) data, or data that is significantly different from the model’s training set. Although calibration and OOD detection are orthogonal problems — e.g., softmax scores can be used directly to detect OOD data despite being poorly calibrated [16] — they are often studied in tandem, where the best calibration methodologies are evaluated with respect to both calibration and the ability to detect OOD data (i.e., by assigning high uncertainty/low confidence to such examples) [6].
Measuring Calibration
Although it is hopefully clear by now that confidence calibration is a useful property, it is not straightforward to measure in comparison to concrete performance metrics like accuracy or loss. Thus, various different metrics for confidence calibration have been proposed over time, each with their own pros and cons. Within this section, I will overview the most widely-used metrics for measuring confidence calibration in order of relevance. For each of these metrics, I will identify whether it is a proper scoring rule — meaning that the optimum score corresponds to a perfect prediction and no “trivial” optimal solutions exist — explain the intuitive meaning of the score, and describe how it can be calculated.
Brier Score [1]
The Brier Score (BS) is a proper scoring rule that measures the squared error between a predicted probability vector and the one-hot encoded true label. Lower scores correspond to more accurate calibration; see the image below for a depiction.
Intuitively, the BS measures the accuracy of predicted probabilities. It can be decomposed into three components — uncertainty (marginal uncertainty over labels), resolution (deviations of individual predictions against the marginal), and reliability (average violation of true label frequencies) — as shown below.
Although the BS is a good metric for measuring calibration of a network’s predictions, it is insensitive to probabilities associated with infrequent events. Thus, utilizing multiple metrics in addition to BS for measuring calibration often provides useful insight.
Expected and Max Calibration Error [2]
Expected calibration error (ECE) computes the difference in expectation between confidence and accuracy. Such a difference in expectation can be computed as shown below.
Although the above expression cannot be computed in closed form, we can approximate it by partitioning model predictions into separate bins based upon their associated confidence scores. Then, the difference between average confidence and accuracy can be computed within each bin, as shown in the image below.
From here, ECE computes the difference between average confidence and accuracy within each bin, then takes a weighted average of these values based upon the relative size of each bin. Maximum Calibration Error (MCE) follows this same process, but is equal to the maximum difference between average confidence and accuracy across bins. See the image below for a more rigorous formulation of ECE and MCE.
For both ECE and MCE, lower scores correspond to better-calibrated predictions. Neither ECE nor MCE are proper scorings rules, meaning that trivial solutions (e.g., predicting uniform, random probability) exist with optimal calibration error. Additionally, due to the binning procedure, neither of these metrics monotonically decrease as predictions improve. Nonetheless, these metrics are commonly used due to their ability to provide simple and interpretable estimates of model calibration. MCE is commonly-used in applications where reliable confidence measures are absolutely necessary (i.e., large mistakes in calibration are detrimental), while ECE provides a more holistic, averaged metric across bins.
Reliability Diagrams. If one wishes to obtain a plot that characterizes calibration error instead of a scalar metric like ECE or MCE, per-bin accuracy and confidence measures can be easily converted into a reliability diagram. Such diagrams depict accuracy on the y-axis and average confidence on the x-axis. Then, the average confidence and accuracy measures within each bin are plotted on the diagram, forming a line plot. Here, perfect calibration would yield a diagonal line on the reliability diagram, where confidence is equal to accuracy within each individual bin; see below for an illustration.
Reliability diagrams are often useful for visualizing the calibration error across all bins. While ECE and MCE aggregate bin statistics into a simple, scalar metric, reliability diagrams enable the properties of each bin to be viewed at once, thus capturing more calibration information in an easily-interpretable plot.
Negative Log-Likelihood
The negative log likelihood (NLL) is a proper scoring rule that can be used to evaluate model uncertainty over held-out data, where lower scores correspond to better calibration. Although typically used as an objective function for training, NLL characterizes the disparity between predicted and actual confidence for the true label, reaching a perfect score of zero when all data is predicted correctly with 100% confidence. See the equation below for a formulation of NLL, where y is the raw vector output of some neural network.
However, NLL overemphasizes tail probabilities, meaning that slight deviations from correct, perfectly-confident predictions can cause large increases in NLL. The impact of this property on neural networks can be readily observed, where NLL (i.e., the objective function) may be quite low with respect to the training set, but incorrect predictions on the test set are made with 100% confidence due to a tendency of the network to make high-confidence predictions in order to minimize NLL (i.e., the “overconfidence” issue mentioned at the beginning of this post) [2].
Entropy
Oftentimes, we may want to evaluate a model’s behavior on data that is from a different distribution than the training set and, therefore, has no true label that is understood by the model (i.e., OOD data). In such a case, none of the previous metrics can be used for evaluation due to the lack of a true label. Instead, the model’s behavior is usually analyzed by measuring the entropy of the output distribution produced by such OOD data.
Intuitively, OOD data should result in network predictions with high entropy, corresponding to a state of uncertainty in which all possible outputs are assigned uniform probability. On the other hand, network predictions for data that is understood well should have low entropy, as the model predicts the correct class with high confidence if it is accurate and properly calibrated. Thus, when evaluating a model over a set of testing examples that contains OOD data, the entropy of predictions made for normal and OOD data should be clearly separated, revealing that the model demonstrates measurable uncertainty on OOD examples.
Calibration Methodologies
Within this section, I will explore numerous methodologies that have been proposed for improving neural network confidence calibration. Some of these methodologies are simple tricks that can be added to the training process, while others require post-processing phases that leverage hold-out validation sets or even require significant changes to the network architecture. In describing each methodology, I will overview their pros and cons, focusing upon whether each methodology is appropriate for use in large-scale deep learning applications.
Temperature Scaling [2]
When the poor calibration of modern deep neural networks was first identified and explored (i.e., the “overconfidence” issue outlined at the beginning of this post), authors attributed the tendency of such networks to make overconfident, wrong predictions to recent developments such as increasing neural network size/capacity, batch normalization, training with less weight decay, and even using the NLL loss (i.e., this loss pushes network predictions towards high confidence due to its emphasis on tail probabilities). Surprisingly, such modern best-practices for neural network training — despite producing networks with impressive performance — were found to produce networks with significantly degraded calibration properties in comparison to previous generations of architectures (e.g., LeNet [7]).
To solve such poor calibration, the authors of [2] explore several different post-hoc calibration techniques that perform calibration after the completion of training by using some hold-out validation set. They find that tuning the softmax temperature of the output layer (i.e., referred to as Platt Scaling in the binary setting [8]) to minimize NLL over the validation set is most effective at calibrating network predictions. Thus, the softmax transformation is modified as shown below with positive-valued temperature T.
Within this expression, large values of T will “soften” the output distribution (i.e., move it towards a uniform distribution), while smaller values of T will place more emphasis on the largest-valued outputs in the distribution. Thus, the T parameter essentially controls the entropy of the output distribution.
By tuning the T parameter over a hold-out validation set to optimize NLL, authors of [2] are able to significantly improve network calibration. However, this calibration process requires a validation dataset and is performed as a separate stage after training. Furthermore, later work finds that such a methodology does not work well for handling OOD data, and completely fails when data being exposed to the network is non-i.i.d. [6]. As a result, the network can still make wrong predictions with high confidence given sufficiently unfamiliar or adversarial data.
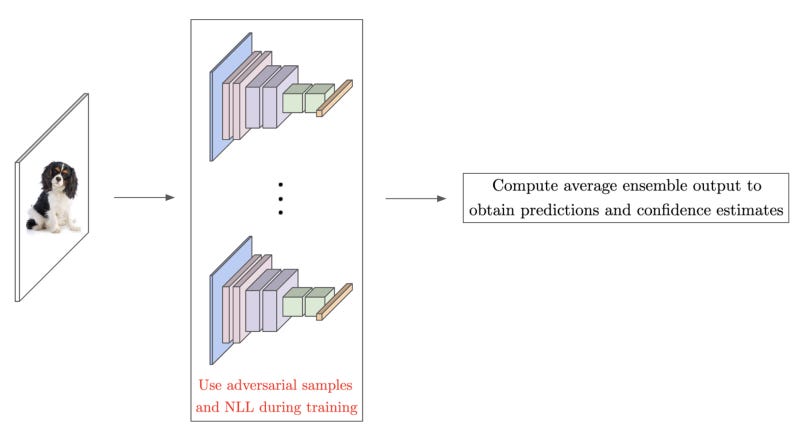
Ensemble-based Calibration [9]
Ensembles — or groups of several, independently-trained networks that are used jointly for prediction — are widely-known to provide improved performance in comparison to individual networks [10]. However, the authors of [9] demonstrated that averaging the predictions of networks within an ensemble can also be used to derive useful uncertainty estimates. In particular, the training procedure is modified by i) using a proper scoring rule (e.g., NLL) as an objective function, ii) augmenting the training set with adversarial examples [11], and iii) training an ensemble of networks; see below for a depiction.
Each network within the ensemble is trained independently and over the full dataset (i.e., with different random initialization and shuffling), meaning that the training of each member within the ensemble can be performed in parallel. Then, by averaging the predictions of the resulting ensemble, one can obtain high-quality uncertainty estimates even on large-scale datasets. Furthermore, such an approach is shown to be robust to shifts in the dataset, allowing OOD examples to be accurately detected. As such, ensemble-based calibration techniques, despite incurring the extra compute cost of handling multiple networks, are simple, highly-robust, and performant.
Mixup [12]
Mixup is a simple data augmentation technique that operates by taking convex combinations of training examples with a randomly-sampled (from a beta distribution) weighting and using such combined samples to train the network; see below for a schematic depiction.
Notably, mixup takes a combination of both the input images and their associated labels. Furthermore, recent work [13] has found that using mixup during training, in addition to providing significant regulation and performance benefits, can result in classification models with improved calibration properties. Such a finding holds even at scale, and Mixup — including its various variants that have been proposed — was even shown to be effective at detecting OOD data [14]. Interestingly, the authors of [13] found that simply mixing the input images is not sufficient for realizing calibration benefits, revealing that mixing of the output labels is essential to calibrating network output. Such a finding is further supported by related work that studies the effect of label smoothing (i.e., increasing the entropy of the label distribution) on network performance and calibration [15].
Bayesian Neural Networks [3]
Bayesian neural networks — motivated by the fact that infinitely-wide neural networks with distributions over their weights converge to Gaussian Processes (and thus have closed-form uncertainty estimates) [4] — can be simply defined as finite neural networks with distributions placed over their weights. Such a formulation offers robustness to overfitting and enables the representation of uncertainty within the network. However, bayesian neural networks, even with the use of newly-developed variational inference techniques, suffer prohibitive compute and memory costs. In fact, the size of the underlying model must usually be doubled to enable proper uncertainty estimates with a bayesian formulation [5]. As such, bayesian neural networks are not yet suitable for large-scale applications, but I recommend anyone interested in this approach to read this wonderful and practical overview.
Dropout as a Bayesian Approximation [5]
As mentioned above, bayesian networks enable reasoning about model uncertainty but are oftentimes prohibitive in terms of computational cost. However, recent work has demonstrated that neural networks trained with dropout [17] are a bayesian approximation of Gaussian Processes. Furthermore, this property can be exploited to generate uncertainty scores for predictions of deep networks by simply i) running multiple random forward passes (with different instantiations of dropout) and ii) averaging the predictions of each forward pass; see below for a depiction of this methodology, which is commonly referred to as Monte Carlo dropout.
Interestingly, this perspective of dropout as an approximation to a Gaussian Process enables robust uncertainty estimation without changing the underlying network or requiring any post-hoc processing. In fact, all that is required is to train a normal network with dropout and perform multiple, random forward passes with dropout at test time, where each of the different forward passes can be parallelized to avoid added latency. Such an approach works quite well in large-scale applications and is shown to both achieve state-of-the-art confidence calibration and detect OOD data with high accuracy. However, the performance of dropout-based calibration is slightly worse than ensemble-based techniques discussed above.
So… What should you use?
Although we have overviewed several methodologies for confidence calibration within this post, one may ask which of them will provide the most benefit in practice. Relevant considerations for such a determination are simplicity, effectiveness, and efficiency. We have seen that methods such as temperature scaling and utilizing uncertainty approximations from Bayesian Neural Networks may not work well at larger scales — e.g., temperature scaling breaks on non-i.i.d. data, while Bayesian Neural Networks are computationally expensive — thus making them less effective in certain scenarios. Other methodologies work quite well and provide impressive calibration results at scale. Thus, given that such approaches are generally effective, one may begin to consider their simplicity and efficiency.
Mixup is a easy-to-implement (i.e., just see the reference implementation in the paper) data augmentation technique that can just be added into training to improve the resulting network’s calibration, making it a low-cost and simple option for calibrating your neural network. Similarly, utilizing an ensemble of networks provides impressive calibration results and is simple to implement (i.e., just train more networks!). But, it introduces the extra computational expense of training multiple networks and using them all for prediction, thus degrading efficiency for both training and prediction in comparison to data augmentation techniques like Mixup. Going further, Monte Carlo dropout does not degrade the efficiency of training and provides impressive uncertainty calibration at scale, but requires multiple forward passes during prediction and is typically outperformed by ensemble-based uncertainty estimation. Thus, the choice of method is typically application-based and depends upon the constraints under which one is operating (e.g., training needs to be fast so use Mixup or Monte Carlo dropout, efficiency is not a concern so use an ensemble, etc.).
Conclusion
Thank you so much for reading this post! I hope you found it helpful. If you have any feedback or concerns, feel free to comment on the post or reach out to me via twitter. If you’d like to follow my future work, you can follow me on Medium. My blog focuses on practical techniques for deep learning, and I try to post two articles about topics ranging from deep learning on video to using online learning techniques for deep networks. Also feel free to check out the content on my personal website if you are interested in my publications and other work. This series of posts was completed as part of my background research as a research scientist at Alegion. If you enjoy this post, feel free to check out the company and any relevant, open positions — we are always looking to discuss with or hire motivated individuals that have an interest in deep learning-related topics!
Bibliography
[1] Brier, Glenn W. “Verification of forecasts expressed in terms of probability.” Monthly weather review 78.1 (1950): 1–3.
[2] Guo, Chuan, et al. “On calibration of modern neural networks.” International Conference on Machine Learning. PMLR, 2017.
[3] Neal, Radford M. Bayesian learning for neural networks. Vol. 118. Springer Science & Business Media, 2012.
[4] Williams, Christopher. “Computing with infinite networks.” Advances in neural information processing systems 9 (1996).
[5] Gal, Yarin, and Zoubin Ghahramani. “Dropout as a bayesian approximation: Representing model uncertainty in deep learning.” international conference on machine learning. PMLR, 2016.
[6] Ovadia, Yaniv, et al. “Can you trust your model’s uncertainty? evaluating predictive uncertainty under dataset shift.” Advances in neural information processing systems 32 (2019).
[7] LeCun, Yann, et al. “Gradient-based learning applied to document recognition.” Proceedings of the IEEE 86.11 (1998): 2278–2324.
[8] Platt, John et al. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in large margin classifiers, 10(3): 61–74, 1999.
[9] Lakshminarayanan, Balaji, Alexander Pritzel, and Charles Blundell. “Simple and scalable predictive uncertainty estimation using deep ensembles.” Advances in neural information processing systems 30 (2017).
[10] T. G. Dietterich. Ensemble methods in machine learning. In Multiple classifier systems. 2000.
[11] I. J. Goodfellow, J. Shlens, and C. Szegedy. Explaining and harnessing adversarial examples. In ICLR, 2015.
[12] Zhang, Hongyi, et al. “mixup: Beyond empirical risk minimization.” arXiv preprint arXiv:1710.09412 (2017).
[13] Thulasidasan, Sunil, et al. “On mixup training: Improved calibration and predictive uncertainty for deep neural networks.” Advances in Neural Information Processing Systems 32 (2019).
[14] Wolfe, Cameron R., and Keld T. Lundgaard. “E-Stitchup: Data Augmentation for Pre-Trained Embeddings.” arXiv preprint arXiv:1912.00772 (2019).
[15] Müller, Rafael, Simon Kornblith, and Geoffrey E. Hinton. “When does label smoothing help?.” Advances in neural information processing systems 32 (2019).
[16] Hendrycks, Dan, and Kevin Gimpel. “A baseline for detecting misclassified and out-of-distribution examples in neural networks.” arXiv preprint arXiv:1610.02136 (2016).
[17] Srivastava, Nitish, et al. “Dropout: a simple way to prevent neural networks from overfitting.” The journal of machine learning research 15.1 (2014): 1929–1958.