Building a Music Recommendation Engine with Probabilistic Matrix Factorization in PyTorch
An explanation of the theory behind probabilistic matrix factorization for recommendation engines, and how it can be implemented in Python.
Recommendation systems are one of the most widespread forms of machine learning in modern society. Whether you are looking for your next show to watch on Netflix or listening to an automated music playlist on Spotify, recommender systems impact almost all aspects of the modern user experience. One of the most common ways to build a recommendation system is with matrix factorization, which finds ways to predict a user’s rating for a specific product based on previous ratings and other users’ preferences. In this article, I will use a dataset of music ratings to build a recommendation engine for music with PyTorch in an attempt to clarify the details behind the theory and implementation of a probabilistic matrix factorization model.
Introduction to Recommendation Systems
In this section, I will attempt to provide a quick, but comprehensive introduction to recommendation systems and matrix factorization before introducing the actual implementation and results for the music recommendation project.
What is a Recommendation System?
To create a recommendation system, we need a dataset that includes users, items, and ratings. Users can be customers buying products from a store, a family streaming a movie from home, or, in our case, even a person listening to music. Similarly, items are the products that a user is buying, rating, listening to, etc. Therefore, the data set for a recommendation system generally has many entries that include a user-item pair and a value representing the user’s rating for that item, such as the data set seen below:
User ratings can be collected either explicitly (asking user for a 5 star ratings, asking whether a user likes a product, etc.) or implicitly (examining purchase history, mouse movements, listening history, etc.). Additionally, the values for ratings could be binary (a user buying a product), discrete (rating a product 1–5 stars), or almost anything else. In fact, the dataset used for this project represents ratings as the total number of minutes a user has spent listening to an artist (this is an implicit rating!). Each of the entries in the data set represents a user-item pairing with a known rating, and, from these known user-item pairings, a recommendation system tries to predict user-item ratings that are not yet known. Recommendations may be created by finding items that are similar to those a user likes (item-based), finding similar users and recommending the stuff they like (user-based), or finding a relationship between user-item interactions as a whole. In this way, the model recommends different items that it believes the user might enjoy that the user has not yet seen.
It’s pretty easy to understand the purpose and value of a good recommender system, but here is a nice figure that I believe summarizes recommendation systems nicely:
What is Matrix Factorization?
Matrix factorization is a common and effective way to implement a recommendation system. Using the previously-mentioned user-item dataset (Figure 1), matrix factorization attempts to learn ways to quantitatively characterize both users and items in a lower-dimensional space (as opposed to looking at every item the user has ever rated), such that these characterizations can be used to predict user behavior and preferences for a known set of possible items. In recent years, matrix factorization has become increasingly popular due to its accuracy and scalability.
Using the data set of user-item pairings, one can create a matrix such that all rows represent different users, all columns represent different items, and each entry at location (i, j) in the matrix represents user i’s rating for item j. This matrix is illustrated in the following figure:
In the above figure, each row contains a single user’s ratings for every item in the set of possible items. However, some of these ratings might be empty (represented by “???”). These empty spots represent user-item pairings that are not yet known, or that the recommendation system is trying to predict. Moreover, this partially-filled matrix, referred to as a sparse matrix, can be thought of as the product of two matrices. For example, the above 4x4 matrix could be created by multiplying two 4x4 matrices with each other, a 4x10 matrix with a 10x4 matrix, a 4x2 matrix with a 2x4 matrix, etc. This process of decomposing the original matrix into a product of two matrices is called matrix factorization.
Matrix Factorization for Recommendation Systems
So, we know that we can decompose a matrix by finding two matrices that can be multiplied together to form our original matrix. But, how does matrix factorization actually work in a recommendation system?
When these two separate matrices are created, they each carry separate information about users, items, and the relationships between them. Namely, one of the matrices will store information that characterizes users, while the other will store information about the items. In fact, every row of the user (left) matrix is a vector of size k that quantitatively describes a single user, while every column of the item (right) matrix is a vector of size k that characterizes a single item. The size of these vectors, k, is called the latent dimensionality (or embedding size), and is a hyperparameter that must be tuned in the matrix factorization model — a larger latent dimentionality will allow for the model to capture more complex relationships and store more information, but can also lead to overfitting.
This idea may seem weird at first, but if you examine closely how the matrices are multiplied to create the user-item matrix, it actually makes a lot of sense — the rating of user i for item j is obtained by finding the inner product of user i’s vector from the left matrix and item j’s vector from the right matrix. Therefore, if these vector embeddings for each user and item are trained to store useful, characteristic information, the inner product can accurately predict a user-item rating based on an item’s characteristics and a user’s preferences for such characteristics, which are all stored in the values of the embedding vector. This concept is illustrated in the following figure:
In the above figure, note how each entry of the product matrix is derived. For example, entry (0, 0) of the user-item matrix, representing user 0’s rating for item 0, is obtained by taking the inner product of the 0th row on the left matrix (the embedding vector for user 0) and the 0th column on the right matrix (the embedding vector for item 0) — this pattern continues for every rating in the user-item matrix. Therefore, as previously described, every rating is predicted by taking the inner product of the corresponding user and item embedding vectors, which is the core idea behind how matrix factorization works for recommendation systems. Using common training methods, like stochastic gradient descent or alternating least squares, these two matrices, and the embedding vectors within them, can be trained to yield a product that is very similar to the original user-item matrix, thus creating an accurate recommendation model.
But wait… didn’t you say Probabilistic Matrix Factorization
Yes, I did! Don’t worry, probabilistic matrix factorization is very similar to what I have been explaining so far. The key difference between normal matrix factorization and probabilistic matrix factorization is the way in which the resulting matrix is created. For normal matrix factorization, all unknown values (the ratings we are trying to predict) are set to some constant (usually 0) and the decomposed matrices are trained to reproduce the entire matrix, including the unknown values. It is not very hard to realize why this might become an issue, as the matrix factorization model is predicting values that we do not actually know and that could be completely wrong. Additionally, how can we predict unknown user-item ratings when we are already training our model to predict a random user-defined constant for all of them?
To solve this problem, we have probabilistic matrix factorization. Instead of trying to reproduce the entire resulting matrix, probabilistic matrix factorization only attempts to reproduce ratings that are in the training set, or the set of known ratings. Therefore, the model is trained using only known ratings, and unknown ratings can be predicted by taking the inner product of the user and item embedding vectors.
Probabilistic Matrix Factorization in PyTorch
Now that you understand the basics behind recommender systems and probabilistic matrix factorization, I am going to outline how a model for such a recommender system can be implemented using PyTorch. If you are unfamiliar with PyTorch, it is a robust python framework often used for deep learning and scientific computing. I encourage anyone who is curious in learning more about PyTorch to check it out, as I heavily use the framework in my research and personal projects.
What are we trying to implement?
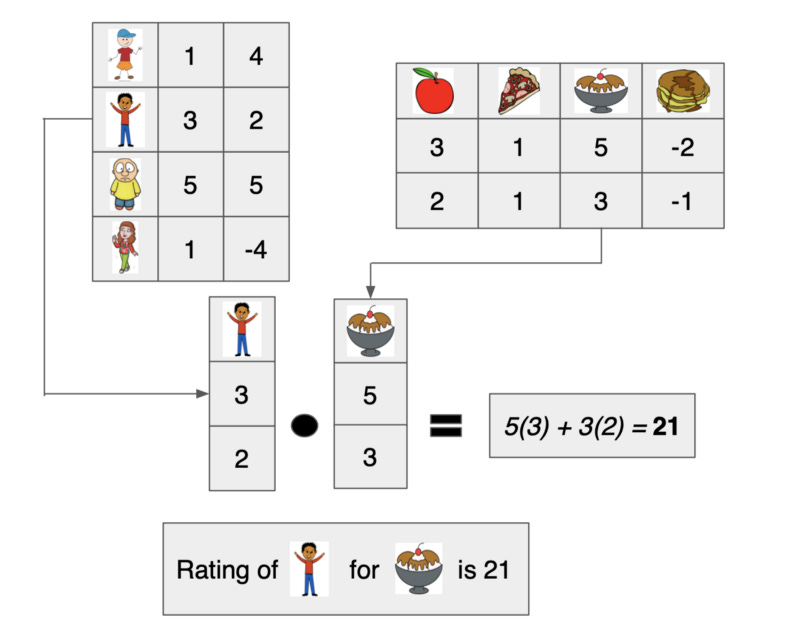
As seen in Figure 4, our model for probabilistic matrix factorization is just two matrices — how simple! One of the matrices will represent the embeddings for each user, while the other matrix will contain embeddings for each item. Each embedding is a vector of k values (k is the latent dimensionality) that describe a user or item. Using these two matrices, a rating prediction for a user-item pairing can be obtained by taking the inner product of the user’s embedding vector and the item’s embedding vector, yielding a single value that represents the predicted rating. Such a process can be observed in the following figure:
As can be seen above, a single rating can be determined by finding the corresponding user and item vectors from the user (left) and item (right) matrices and computing their inner product. In this case, the result shows that the chosen user is a big fan of ice cream — what a surprise! However, it should be noted that each of these matrices are randomly initialized. Therefore, in order for these predictions and embeddings to accurately characterize both users and items, they must be trained using a set of known ratings so that the accuracy of predictions generalizes to ratings that are not yet known.
Such a model can be implemented with relative ease using the Embedding class in PyTorch, which creates a 2-dimensional embedding matrix. Using two of these embeddings, the probabilistic matrix factorization model can be created in a PyTorch module as follows:
The matrix factorization model contains two embedding matrices, which are initialized inside of the model’s constructor and later trained to accurately predict unknown user-item ratings. In the forward function (used to predict a rating), the model is passed a mini-batch of index values, which represent the identification numbers (IDs) of different users and items. Using these indices, passed in the “cats” parameter (an Nx2 matrix) as user-item index pairs, the predicted ratings are obtained by indexing the user and item embedding matrices and taking the inner product of the corresponding vectors.
Adding Bias
The model from Figure 6 is lacking an important feature that is needed for the creation of a powerful recommendation system — the bias term. The bias term is basically a constant value that is assigned to each user and item in the system. When the predicted rating for a user-item pairing is computed, the bias for both the user and item are added to the predicted rating value. This process can be observed below:
As can be seen above, the amount of change needed to add bias into the model is quite small. An extra value for each user/item must be tracked and added to the result of each prediction made by the model. These bias values will be trained alongside the actual embeddings to yield accurate predictions.
Adding bias to the model in PyTorch requires that two extra embeddings be created — one for the user bias and one for the item bias. These embeddings will have a single column and each row will represent the bias value for the user or item with an ID corresponding to that row index. These bias values, similarly to the embedding vectors, should then be found using the indices passed in the “cats” parameter in the forward method. The implementation can be seen below:
As seen in the above implementation, two new embeddings were added into the model for the user and item bias. The values from these bias vectors were then added into the result of each prediction inside of the forward method.
Now, a complete probabilistic matrix factorization model has been implemented — this can be used to create very powerful recommendation systems that can add value to almost any business. However, you might be thinking that this model looks pretty similar to the last one, so why do we bother adding bias into the model? Does it really make it any better?
Why do we even need bias?
We will first consider bias in terms of each user. If a user has a very high bias value, what does this mean? Typically, users are assigned high bias values if they often give high ratings to items, while users that often assign low ratings are given lower bias values. This makes sense, because a user that rates items very high on average should be biased towards higher ratings and vice versa. Such bias can, in turn, allow the model to separate user tendencies in rating items from their actual item preferences by just learning a proper bias value.
Similarly, items that are given typically high ratings are assigned large biases, while items with low average ratings are given low values. This allows items that are highly rated by users to be biased towards high ratings, as most users tend to enjoy such items, and vice versa. This can be visualized in the following figure:
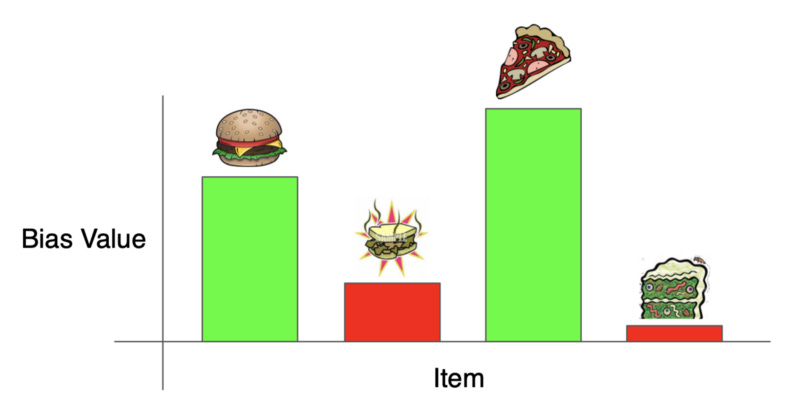
The average ratings of users or items create unneeded noise within the dataset. By including bias, the model to can learn to characterize users and items separately from such noise, allowing the user and item embeddings to more accurately reflect the properties and preferences of each user or item.
Creating a Music Recommendation System
Now that the model has been created, I am going to use it to create a music recommendation system. For this project, I utilized a data set of users and musicians, where each user-musician pairing is assigned a value based on the amount of time a user has spent listening to an artist. I then used the probabilistic matrix factorization model from Figure 8 to create a music recommender model from this dataset.
Simple EDA
I began this experiment by doing some simple exploratory data analysis (EDA) on the data set using pandas. The first step in my analysis was examining a sample of the data and checking for any null values. There were no null values present, and the data appeared as follows:
This data set appears to resemble a normal recommendation system dataset, which is (obviously) well suited for our model. Each datum contains a userID, an artistID, and a value representing the user’s rating of that artist. However, the weight values in this data set, representing the user-artist ratings, are quite large because they are determined by the number of minutes a user has spent listening to an artist. A typical recommendation system dataset contains ratings between 1–5, binary ratings (i.e. 0 or 1), or something along these lines. Therefore, the rating values in this data set should be normalized such that they are within a smaller range, which can be done as follows:
After weight values were normalized, I began to examine the sparsity of the dataset, or the number of known ratings in comparison to the number of possible user-item combinations. Originally, only .2% of possible ratings within the data set were known, which is quite sparse and could negatively impact the accuracy of the model. Therefore, I chose to filter the data set to only include only users that had rated at least five artists.
After the above operation was performed on the dataset, it increased the density of the data set to 1.3%, which, while still relatively sparse, will allow the matrix factorization model to make more accurate predictions.
After these changes were made, there was one last change I wanted to make before fitting the model. Within this data set, each user and artist is assigned a unique ID. However, in order to make using the recommendation model easier, I wanted to make all of these IDs contiguous, such that they can be used to index into the embedding matrices. This can be accomplished with the following code, which ensures that all users and artists are given a contiguous, unique ID:
This code creates a mapping, for both users and items, from the original ID to the new contiguous ID, such that all IDs fall within the range [0, total number of users/artists]. By performing this conversion, the IDs for both users and artists can be used as an index into embedding matrices for easy look up and quick predictions.
Hyperparameter Selection/Tuning
Now that the data has been filtered and preprocessed, the recommendation model can actually be trained. However, training the model has a couple of hyper-parameters that must be set properly: the learning rate and the latent dimensionality.
To determine the optimal learning rate, I utilized an adaptive learning rate selection technique described in the fast.ai deep learning course. This technique trains the model for several iterations, increasing the learning rate used for updating the model’s parameters on every iteration. The loss is then recorded for each iteration and displayed on a graph, as seen in the following figure:
In the above figure, the optimal initial learning rate is represented by the largest value for the learning rate before the loss begins to increase, which, in this case, was around 0.1. Therefore, the learning rate was initially set to .1 when the model was trained.
Determining the optimal latent dimensionality was done through grid search using values of 20, 30, 40, 50, and 60. After running three epochs of training with each of these embedding sizes, the results were as follows:
After performing the grid search, an embedding size of 40 was chosen for the music recommendation system, as it had the minimal validation loss after three epochs of training.
Fitting the Model
Now that the hyper-parameters have been selected, the model can be trained. Training was done three epochs at a time, and the learning rate was reduced by a factor of ~2 every three epochs until the model converged. By gradually decreasing the learning rate, a simple learning rate scheduler was created that allowed the model to fine-tune its parameters and minimize loss as much as possible. The loss for the model throughout the entire training process can be seen in the following figure:
The model was trained for 3 epochs with learning rates of .1, .05, .01, .005, and .001, resulting with a final MSE loss of 0.75. In other words, all predictions made for a user-artist pair had an average error of about 0.86. Given that all ratings in the training and testing datasets are within the range [0, ~60], an average error of .86 is relatively low, which hints that the model fit the data relatively well!
Extra Analysis
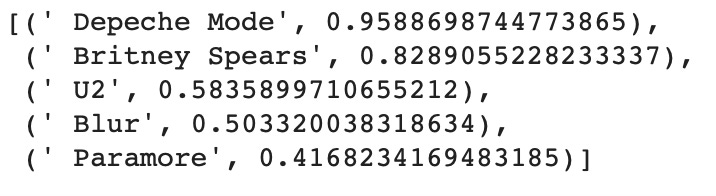
Although probabilistic matrix factorization works well for predicting user-item ratings, one of the most interesting aspects of the model is the embeddings that it creates to quantitatively describe each user and item. These embeddings can be used to gain insights about users or products, as input into other machine learning models (such as a deep neural network), or even to determine which items users enjoy the most! Just for fun, I performed some extra analysis on the embeddings that were created through training this model, in order to see if they carried any interesting information. More specifically, I examined the bias values produced for each artist in the dataset, which characterize, in general, all users’ preference for each artist. After sorting bias values with their associated artists, it yielded the following result:
As can be seen, the artists with the highest bias values are well-known and successful musicians, such as Britney Spears and U2, thus demonstrating the usefulness of information contained within the model’s embeddings!
Conclusion
Thank you so much for reading, and I hope you now have a better understanding of recommendation systems, how they work, and how you can implement probabilistic matrix factorization yourself! If you are interested in exploring the extra details of this project, I encourage you to check out the GitHub repository that I created, which contains the full notebooks with all of my codes used in implementing the recommendation system. Additionally, feel free to follow me on LinkedIn or on Medium to stay updated with my future articles and work.
Sources/Citations
[1] https://johnolamendy.wordpress.com/2015/10/14/collaborative-filtering-in-apache-spark/