This newsletter is supported by Alegion. At Alegion, I work on a range of problems from online learning to diffusion models. Feel free to check out our data annotation platform or contact me about potential collaboration/opportunities!
If you like this newsletter, please subscribe, share it, or follow me on twitter. Thank you for your support!
Prior research in computer graphics and 3D computer vision has proposed numerous approaches for representing 3D shapes. Such methods are useful for:
storing memory-efficient representations of known shapes
generating new shapes
fixing/reconstructing shapes based on limited or noisy data
Beyond classical approaches, deep learning—or, more specifically, generative neural networks—can be used to represent 3D shapes. To do this, we can train a neural network to output a representation of a 3D shape, allowing representations for a variety of shapes to be indirectly stored within the weights of the neural network. Then, we can query this neural network to produce new shapes.
Within this post, we will study one of such methods, called DeepSDF [1], that uses a simple, feed-forward neural network to learn signed distance function (SDF) representations for a variety of 3D shapes. The basic idea is simple: instead of directly encoding a geometry (e.g., via a mesh), we train a generative neural network to output this geometry. Then, we can perform inference to (i) obtain the direct encoding of a (potentially new) 3D shape or (ii) fix/reconstruct a 3D shape from noisy data.
why is this paper important? This post is part of my series on deep learning for 3D shapes and scenes. This area was recently revolutionized by the proposal of NeRF [2], which enables accurate 3D reconstructions of scenes from a few photos of different viewpoints; see above. With a NeRF representation, we can produce an arbitrary number of synthetic viewpoints of this scene or even generate 3D representations of relevant objects; see below.
DeepSDF is a background method that is referenced by NeRF. Currently, we are surveying prior work that is relevant to understanding more modern methods. We will eventually build up to an understanding of NeRF (and other papers that follow it)!
Background
Before diving into how DeepSDF works, there are a few background concepts that we will need to understand. First, we’ll talk a bit about how 3D shapes are usually represented, as well as how a signed distance function (SDF) can be used to represent a 3D shape. Then, we’ll talk about feed-forward neural networks, an incredibly simple deep learning architecture that is used heavily by research in 3D modeling of shapes.
representing 3D shapes
When considering how to store a 3D shape in a computer, we have three options: a point cloud, mesh, or voxels. Each of these representations have different benefits and limitations, but they are all valid methods of directly representing a 3D shape. Let’s get a basic idea of how they work.
point cloud. Point clouds are pretty easy to understand. As we might infer from the name, they just store a group of points with [x, y, z] coordinates in space, and these points are used to represent an underlying geometry; see below.
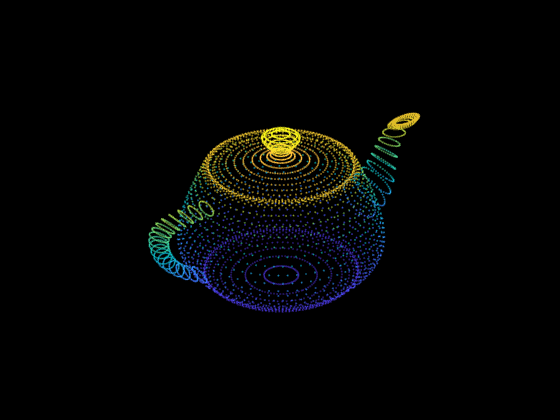
Point clouds are useful because they closely match the type of data we would get from sensors like LiDAR or depth-sensing cameras. But, point clouds do not provide a watertight surface (i.e., a shape with one, closed surface).
mesh. One 3D representation that can provide a watertight surface is a mesh. Meshes are 3D shape representations based upon collections of vertices, edges, and faces that describe an underlying shape. Put simply, a mesh is just a list of polygons (e.g., triangles) that, when stitched together, form a 3D geometry.
voxel-based representation. Voxels are just pixels with volume. Instead of a pixel in a 2D image, we have a voxel (i.e., a cube) in 3D space. To represent a 3D shape with voxels, we can:
Divide a section of 3D space into discrete voxels
Identify whether each voxel is filled or not
Using this simple technique, we can construct a voxel-based 3D object. To get a more accurate representation, we can just increase the number of voxels that we use, forming a finer discretization of 3D space. See below for an illustration of the difference between point clouds, meshes, and voxels.
signed distance functions
Directly storing a 3D shape using a point cloud, mesh, or voxels requires a lot of memory. Instead, we will usually want to store an indirect representation of the shape that’s more efficient. One approach for this would be to use a signed distance function (SDF).
Given a spatial [x, y, z] point as input, SDFs will output the distance from that point to the nearest surface of the underlying object being represented. The sign of the SDF’s output indicates whether that spatial point is inside (negative) or outside (positive) of the object’s surface. See the equation below.
We can identify the surface of a 3D object by finding the locations at which the SDF is equal to zero, indicating that a given point is at the boundary of the object. After finding this surface using the SDF, we can generate a mesh by using algorithms like Marching Cubes.
why is this useful? At a high level, SDFs allow us to store a function instead of a direct representation of the 3D shape. This function is likely more efficient to store, and we can use is to recover a mesh representation anyways!
feed-forward neural networks
Many highly-accurate methods for modeling 3D shapes are based upon feed-forward network architectures. Such an architecture takes a vector as input and applies the same two transformations within each of the network’s layers:
Linear transformation
Non-linear activation function
Though the dimension of our input is fixed, two aspects of the network architecture are free for us to choose: the hidden dimension and the number of layers. Variables like this that we, as practitioners, are expected to set are called hyperparameters. The correct setting of these hyperparameters depends upon the problem and/or application we are trying to solve.
the code. There is not much complexity to feed-forward networks. We can implement them easily in PyTorch as shown below.
| import torch | |
| class FFNN(torch.nn.Module): | |
| def __init__(self, input_size, hidden_size, output_size, num_layers): | |
| super().__init__() | |
| self.input_size = input_size | |
| self.hidden_size = hidden_size | |
| self.output_size = output_size | |
| self.num_layers = num_layers | |
| self.layers = [ | |
| torch.nn.Linear(self.input_size, self.hidden_size), | |
| torch.nn.ReLU(), | |
| ] | |
| for i in range(self.num_layers - 1): | |
| self.layers.append(torch.nn.Linear(self.hidden_size, self.hidden_size)) | |
| self.layers.append(torch.nn.ReLU()) | |
| self.layers.append(torch.nn.Linear(self.hidden_size, self.output_size)) | |
| self.layers = torch.nn.Sequential(*self.layers) | |
| def forward(self, x): | |
| return self.layers(x) |
DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation [1]
Prior research in computer graphics and 3D computer vision has proposed numerous classical approaches for representing 3D shapes and geometries. In [1], authors propose a deep learning-based approach, called DeepSDF, that uses a neural network to learn a continuous SDF for a broad class of shapes. Put simply, this means that we can encode a SDF-based representation of multiple different types of 3D shapes using a single, feed-forward neural network, allowing such shapes to be represented, interpolated or even completed from partial data; see above.
The idea behind DeepSDF is simple: we want to use a neural network to perform regression directly on the values of an SDF. To do this, we train this model over point samples from the SDF (i.e., individual [x, y, z] points with an associated SDF value). If we train a network in this way, then we can easily predict the SDF values of query positions, as well as recover a shape’s surface by finding the points at which the SDF is equal to zero.
how do we represent the shape? More specifically, consider a single shape, from which we sample a fixed number of 3D point samples with SDF values. We should note here that taking more point samples would allow the shape to be represented with higher-precision, but this comes at the cost of increased compute costs.
In the equation above, x is a vector containing [x, y, z] coordinates, while s is the SDF value associated with these coordinates for a given shape.
training the neural network. From here, we can directly train a feed-forward neural network to produce the SDF value s given x as input by training over these sample pairs using an L1 regression loss. Then, the resulting model can output accurate SDF values to represent the underlying shape; see the left subfigure below.
The limitation of such a model is that it only represents a single shape. Ideally, we would want to model a variety of shapes with a single neural network. To accomplish this, we can associate a latent vector (i.e., “Code” in the figure above) with each shape. This is a low-dimensional vector that is unique to each shape that is stored within our neural network. This latent vector can be added as an input to the neural network to inform the network that it is producing output for a particular shape. This simple trick allows us to represent multiple shapes within a single model (this saves a lot of memory!); see the right subfigure above.
The final question we might be asking is: how do we obtain this latent vector for each shape? In [1], the authors do this by proposing an auto-decoder architecture that (i) adds the latent vector to the model’s input and (ii) learns the best latent vector for each shape via gradient descent during training; see below.
Typically, latent vectors are learned via an autoencoder architecture, but this requires the addition of an extra encoder module that incurs extra computational expense. The authors in [1] propose the auto-decoder approach to avoid this extra compute. The difference between these approaches is shown below.
producing a shape. To perform inference with DeepSDF, we must:
Start with a sparse/incomplete set of SDF value samples
Determine the best possible latent vector from these samples
Perform inference with our trained neural network over a bunch of different points in 3D space to determine SDF values
From here, we can visualize the shape represented by DeepSDF with algorithms like Marching Cubes that discretize 3D space and extract an actual 3D geometry based on these SDF values.
the data. DeepSDF is trained and evaluated using the synthetic ShapeNet dataset. In particular, its performance is measured across four tasks.
Representing shapes in the training set
Reconstructing unseen (test) shapes
Completing partial shapes
Sampling new shapes from the latent space
For the first three tasks, we see that DeepSDF tends to outperform baseline methodologies consistently, revealing that it can represent complex shapes with high accuracy and even recover shapes from incomplete samples quite well. This is quite remarkable given that we are storing numerous 3D shapes within a single, memory-efficient neural network; see below.
We can also interpolate the embedding space of a DeepSDF model to produce coherent results. This allows us to do things like find the average shape between a truck and car; see below.
From these results, we can see that interpolation between latent vectors yields a smooth transition between shapes, revealing that the continuous SDFs embedded by DeepSDF are meaningful! Common features of shapes—such as truck beds or arms of chairs—are captured within the representation leveraged by DeepSDF. This is quite remarkable for such a simple, feed-forward network.
Takeaways
DeepSDF is a feed-forward, generative neural network that we can use to represent and manipulate 3D shapes. Using this model, we can easily perform tasks like generate the mesh representation of a shape, recover an underlying shape from incomplete or noisy data, and even generate a new shape that is an interpolation of known geometries. The benefits and limitations of DeepSDF are outlined below.
lots of compression. To store 3D geometries in a computer, we can use mesh or voxel representations. To avoid the memory overhead of directly storing shapes like this, we can use a generative models like DeepSDF. With such an approach, we no longer need the direct mesh encoding of a geometry. Instead, we can use DeepSDF—a small neural network that is easy to store—to accurately generate meshes for a variety of shapes.
fixing a broken geometry. Given partial or noisy representation of an underlying shape, DeepSDF can be used to recover an accurate mesh; see below. In comparison, most prior methods cannot perform such a task—they require access to a full 3D shape representation that matches the type of data used to train the model.
interpolating the latent space. Deep SDF can represent a lot of different shapes and embed their properties into a low-dimensional latent space. Plus, experiments show that this latent space is meaningful and has good coverage. Practically, this means that we can take latent vectors (i.e., vector representations of different objects), linearly interpolate between them, and produce a valid, novel shape. We can easily use this to generate new shapes that have a variety of interesting properties.
limitations. DeepSDF is great, but it always requires access to a (possibly noisy or incomplete) 3D geometry to run inference. Plus, searching for the best possible latent vector (i.e., this must always be done before performing inference due to the auto-decoder approach) is computationally expensive. In this way, the inference abilities of DeepSDF are somewhat limited. To summarize, the approach is slow and cannot generate new shapes from scratch, which leaves room for improvement in future work.
new to the newsletter?
Hello! I am Cameron R. Wolfe, a research scientist at Alegion and PhD student at Rice University. I study the empirical and theoretical foundations of deep learning.
This is the Deep (Learning) Focus newsletter, where I help readers to build a deeper understanding of topics in deep learning research via series of short, focused overviews of popular papers on that topic. Each overview contains explanations of all relevant background information or context. A new topic is chosen (roughly) every month, and I overview two papers each week (on Monday and Thursday). If you like this newsletter, please subscribe, share it with your friends, or follow me on twitter!
bibliography
[1] Park, Jeong Joon, et al. "Deepsdf: Learning continuous signed distance functions for shape representation." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.
[2] Mildenhall, Ben, et al. "Nerf: Representing scenes as neural radiance fields for view synthesis." Communications of the ACM 65.1 (2021): 99-106.
[3] Hoang, Long, et al. "A deep learning method for 3D object classification using the wave kernel signature and a center point of the 3D-triangle mesh." Electronics 8.10 (2019): 1196.