Program-Aided Language Models
We know LLMs can write code. What if they can run it too?
This newsletter is presented by Gretel, a generative AI platform for multi-modal synthetic data. Gretel’s APIs automatically fine-tune models to generate synthetic data on demand, while protecting privacy and maintaining the utility/accuracy of the original data. Our synthetic data platform solves the data bottleneck problem for developers, data scientists, and AI/ML researchers across multiple modalities including tabular, time-series, relational, language and image. Sign up for a free Gretel account today.
Sponsor the newsletter | Follow me on Twitter | My contact info
Although Large Language Models (LLMs) are used for a variety of applications, they have typically struggled to solve reasoning-based tasks. This issue was significantly diminished with the advent of prompting techniques like Chain of Thought and Least-to-Most prompting. At a high level, these techniques encourage reasoning behavior in LLMs by providing examples of problem-solving rationales within the model’s prompt. Then, the model can learn to output such rationales and produce a step-by-step solution to the underlying problem. Notably, this is a prompting-only approach that requires no fine-tuning, revealing that LLMs are capable of reasoning given a prompt with sufficient context.
Despite the effectiveness of techniques like chain of thought prompting, the LLM is expected to produce both a problem-solving chain of thought and a final answer. Interestingly, such an approach leads to peculiar failure cases in which the LLM may produce an accurate rationale for solving a problem but still generate an answer that is incorrect. Usually, such errors are due to simple mistakes (e.g., poor arithmetic). To solve this problem, recent research has explored a programatic approach that encourages the LLM to generate chains of thought with both natural language and code components. Then, the LLM can run this code via an external interpreter to obtain needed outputs.
To understand why such an approach would be useful, we should note that many issues with which LLMs struggle (e.g., arithmetic errors, inability to evaluate complex expressions, etc.) can be easily expressed and solved inside of a program. As a result, using chain of thought-style prompts on LLMs with coding abilities (e.g., Codex) allows us to merge the benefits of LLMs with the computational capabilities of an arbitrary Python program! More specifically, the LLM can be encouraged to generate a problem-solving rationale that contains both natural language and code components, producing a script that can be run by an external interpreter to compute the final output for a problem. Such an approach, which we will explore in this overview, is massively beneficial to the accuracy and reliability of LLMs in solving reasoning-based tasks.
Background Information
Despite the incredible abilities of modern LLMs, these models are all based upon a simple pre-training procedure that performs next-token prediction over a large amount of unlabeled textual data. Although we can tweak the details of this procedure (e.g., the type or mixture of data being used), the fundamental pre-training approach of most LLMs remains fixed. We just simply i) sample some text from the pre-training corpus and ii) teach the model to accurately predict the next word/token in the corpus. That’s it! This simple and profound approach lays the foundation for all of modern language modeling.
But… there are a few more tricks and lessons learned from years of research that allow us to make language models as powerful as ChatGPT or GPT-4. Most models use the same decoder-only architecture, but creating a high-performing language model cannot be done via pre-training alone. We need:
Sufficient scale (i.e., large model and pre-training dataset).
Behavioral refinement via supervised fine-tuning (SFT) and reinforcement learning from human feedback (RLHF) [11, 12].
[Optional] Domain Specialization (i.e., fine-tuning the model on a specific type of data, such as code or dialogue).
If we perform all of these steps correctly, we can create a powerful foundation model that is capable of solving a variety of tasks via textual prompts. Notably, most of a language model’s knowledge and information is learned via pre-training (see “Training process” section here), but these extra refinement steps taken after pre-training make LLMs much more steerable and interesting; see below.
what are LLMs bad at? Language models achieve impressive performance in a variety of different applications, but they are not perfect. These models have known limitations, such as:
Difficulty adding large numbers
Inability to evaluate/solve complex equations
Trouble with reasoning over iterative processes
For example, if we prompt an LLM with a description of the Fibonacci sequence then ask it to compute the 100th number, there is a high likelihood that it will fail! Why is this the case? Well, we know that LLMs struggle with performing arithmetic, and solving the Fibonacci sequence (unless the model uses brute force memorization) requires many, iterative additions between two numbers. If the model has a 95% chance of performing this addition correctly during each iteration, then the 100th Fibonacci number has a <1% chance of being correct!
quick disclaimer. The recent release of GPT-4 has made claims about LLM limitations more difficult to make. For example, GPT-4 is completely capable of solving for the 100th Fibonacci number and can even evaluate some (relatively) complex equations with minimal prompting effort; see below.
With this in mind, any statement about LLM capabilities needs to be taken with a grain of salt. This space is rapidly evolving and models are becoming more and more capable and impressive (literally) every day.
Teaching LLMs how to code
As mentioned above, one (optional) part of creating a high-performing LLM is domain specialization. After pre-training, LLMs are quite generic and capable of only a single task—next-token prediction. If we want an LLM that is specialized within a certain domain or great at performing a specific task (e.g., information-seeking dialogue or writing screenplays), we need to fine-tune the model on a lot of data that demonstrates correct behavior for this task. One of the most successful applications of this technique, which is especially relevant to this overview, is for creating language models that can write code.
Similarly to how large amounts of textual data can be downloaded from the internet for pre-training a language model normally, we can download large amounts code from public sources (e.g., GitHub) for training LLMs, which makes coding a particularly perfect application of specialized LLMs. One notable example of such a model is Codex [4], which is trained using a combination of unlabeled textual data and code downloaded from the internet. Given a Python docstring, Codex is tasked with generating a working Python function that performs the task outlined in the docstring; see above.
Codex performs incredibly well on human-curated coding tasks (see above) and is even used to power the GitHub Copilot coding assistant, revealing that LLMs can be applied to more than just natural language! We can also apply them to many other problems that follow a similar structure. In this case, we use further language model pre-training over a code dataset to adapt a pre-trained LLM to a new domain. Notably, Codex is capable of generating both code and natural language-based output, making it a particular versatile and useful LLM. Plus, creating this domain-specific model is relatively simple—we just need a lot of code for training.
Chain of Thought (CoT) Prompting
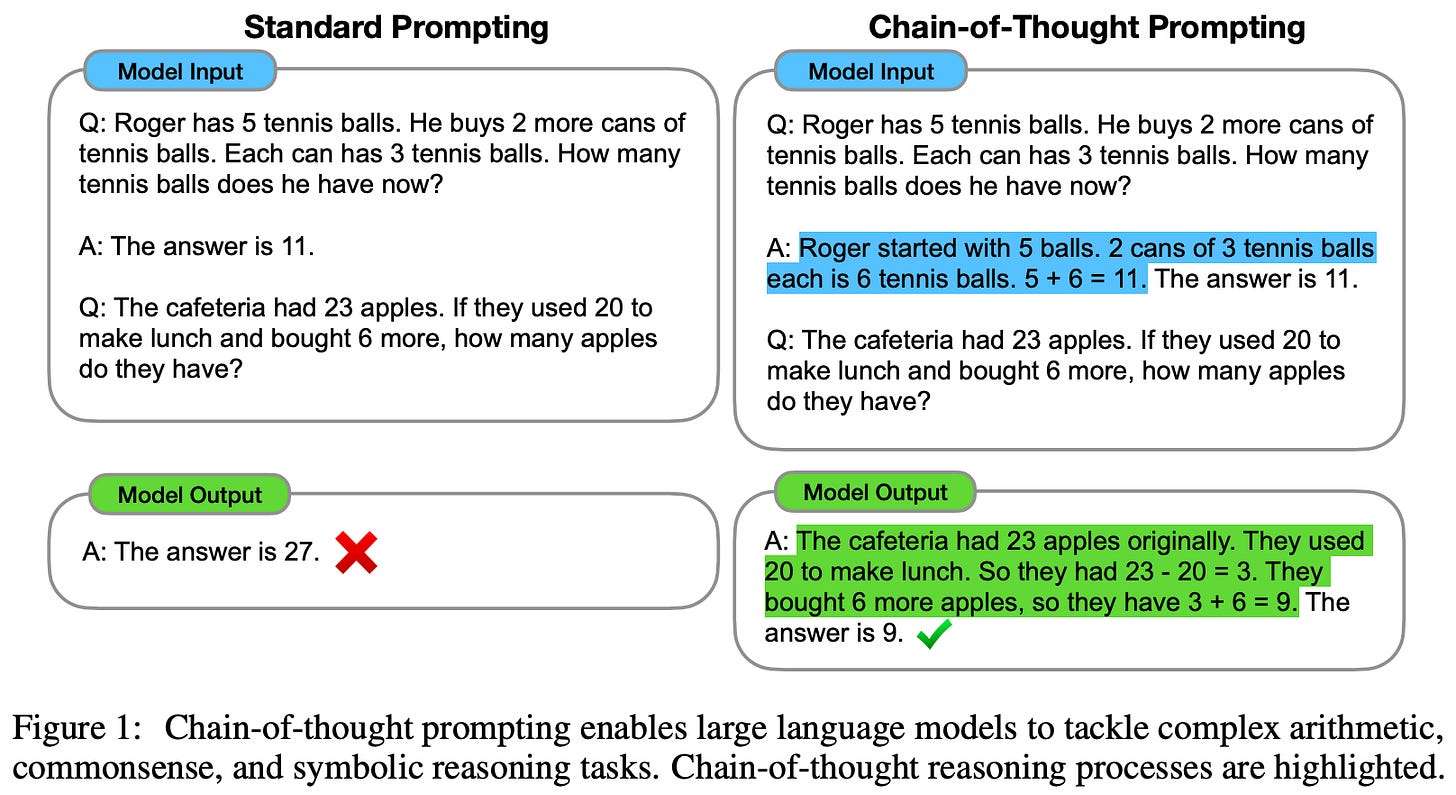
Beyond the limitations outlined previously, LLMs were initially criticized for their inability to solve reasoning tasks. However, research in this area has led to breakthrough techniques like CoT prompting [3] that enable LLMs to solve reasoning-based tasks quite accurately. The idea behind CoT prompting is simple. We just use few-shot learning to teach the LLM how to output a problem-solving rationale that explains its answer—in detail—for any reasoning task; see below. Such an approach is incredibly practical because we only have to generate a few examples of problem-solving rationales to include in the prompt, whereas prior work curated entire datasets of such rationales for fine-tuning.
Unlike teaching an LLM how to code, we see with CoT prompting that such models are capable of solving reasoning tasks without any fine-tuning! Instead, we just need to adopt a better prompting approach that “unlocks” the LLM’s ability to solve complex reasoning tasks.
“Large pretrained language models have built in reasoning capabilities, but they need specific prompts to unleash their power.” - from [13]
Given that we have learned a lot about CoT prompting and its many variants in prior overviews, I will not extensively explore the idea here. However, there is one notable aspect of CoT prompting that we should notice—the LLM is expected to both i) generate a chain of thought and ii) extract the final answer from this chain of thought. Although CoT prompting is effective, we might begin to wonder: is relying on the LLM to accurately solve both of these steps actually a good idea?
Decoupling Reasoning and Computation within LLMs
We know that language models are capable (given a correct prompting approach) of providing an accurate problem-solving rationale or detailed explanation of their output. However, generating a correct rationale does not mean the LLM will solve a problem correctly! What if the LLM makes a small arithmetic error when producing its final answer? Given fundamental limitations of LLMs, techniques like CoT prompting commonly encounter frustrating failure cases in which the model produces an accurate rationale but outputs an incorrect, final answer. Errors of this kind are typically referred to as the compositionality gap for LLMs.
“We measure how often models can correctly answer all subproblems but not generate the overall solution, a ratio we call the compositionality gap.” - from [16]
Within this section, we will explore recent research that attempts to solve this issue by leveraging the unique skills of LLMs that have been trained on code (e.g., Codex [4]) to write coherent and functional programs. We can rely on LLMs to generate a problem-solving rationale. But, instead of asking the LLM to produce an actual answer, we just prompt the model to generate a program associated with the rationale that, when executed using a separate code interpreter, can generate the final answer. Thus, our rationale becomes a hybrid between code and language—basically a Python script with informative comments!
Program-Aided Language Models (PaL)
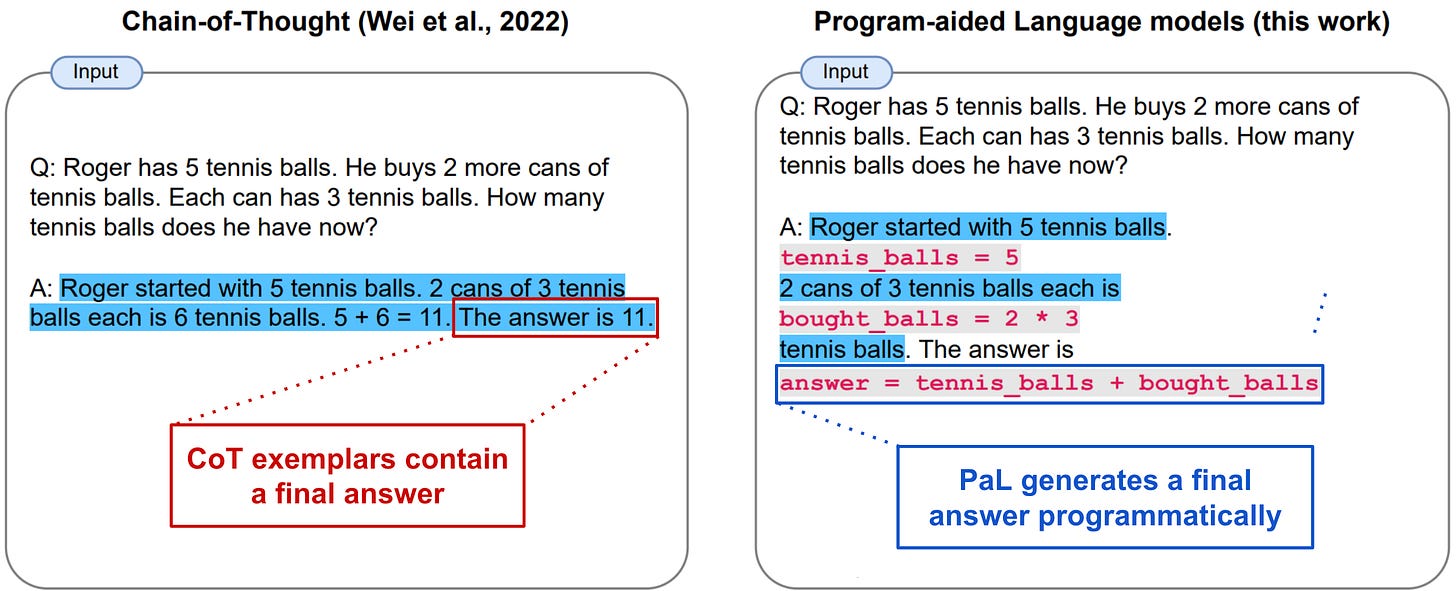
In [1], authors propose a CoT-inspired technique, called Program-Aided Language Models (PaL), that uses an LLM to decompose reasoning-based problems into a step-by-step, problem solving rationale. However, this rationale contains both natural language and (Python-based) programatic components. After such a hybrid rationale has been generated, we can solve the problem by executing the program-based portion of the prompt via a Python interpreter. The goal of such an approach is to eliminated instances where the LLM generates a correct reasoning chain but still produces an incorrect final answer.
“This bridges an important gap in chain-of-thought-like methods, where reasoning chains can be correct but produce an incorrect answer.” - from [1]
With PaL, we can use the LLM to generate a problem-solving rationale, but the process of computing the final solution (i.e., this is the part with which models typically struggle!) is delegated to a code interpreter, eliminating the potential for arithmetic or logical mistakes. As a result, the LLM only needs to learn how to generate a problem-solving rationale—the solution is derived programatically. We can teach the LLM to generate such a hybrid rational via few-shot learning. For this to work, however, we need an LLM that has been pre-trained on both natural language and code (e.g., Codex [4]).
understanding PaL. At a high level, the approach adopted by PaL is quite similar to CoT prompting. We use a few-shot prompting approach that provides several examples of problems being decomposed into an associated rationale. The main difference between CoT and PaL is that the rationales used within PaL are comprised of interleaved natural language and programatic statements; see below.
Each step in the reasoning process with PaL is augmented with a programatic statement. Then, when these programatic statements are synthesized, they can be executed via a separate Python interpreter to generate a final answer (i.e., done via a single, post-hoc execution). PaL is teaching the LLM (via few-shot learning) to generate a program that solves the desired question in a step-by-step manner. Interestingly, authors in [1] encourage the LLM to generate natural language-based intermediate steps by exploiting the Python comment syntax (i.e., the # character), which enables language-based components to be inserted into a generated program. In other words, we are teaching the LLM to solve reasoning task via a step-by-step program with informative comments!
Unlike CoT prompting, few-shot examples used by PaL contain no final solution. Rather, exemplars are just programs with interleaved natural language statements (and nothing else!). The generation of the final solution is delegated to the Python interpreter, so the LLM never needs to learn how to perform this step; see above.
Going further, authors in [1] observe that providing meaningful names to variables used within the program is beneficial. Such a finding indicates that the reasoning process proposed by PaL is a true hybrid approach that merges language and program-based components. Forming symbolic links between entities within programming and language modalities is important; see below.
does this work well? PaL is evaluated on a variety of symbolic, mathematical, and algorithmic reasoning tasks, where it is shown to mitigate many of the common problems encountered with CoT prompting. The proposed method is compared to both standard few-shot learning (called “direct” prompting in [1]) and CoT prompting. On mathematical reasoning tasks, PaL with Codex [4] easily outperforms prior prompting approaches with a variety of different models. Notably, PaL even outperforms Minerva [5], an LLM that was explicitly fine-tuned over a large amount of quantitative reasoning data; see below.
From the table above, we should also notice that PaL using Codex achieves state-of-the-art performance on GSM8K, surpassing the performance of PaLM-540B (i.e., much larger model!) with CoT by 15% absolute top-1 accuracy. Interestingly, authors in [1] point out that GSM8K is mostly focused upon math word problems with smaller numbers (i.e., 50% of numbers are between 0-8) and propose GSM-Hard—a version of this dataset with larger numbers. On the harder dataset, PaL achieves a nearly 40% improvement in absolute top-1 accuracy relative to PaLM with CoT prompting, revealing that program-aided prompting is superior for problems that require complex arithmetic with large numbers.
On symbolic and algorithmic reasoning tasks, PaL again provides a significant benefit; see above. In fact, PaL comes close to completely solving four of the five datasets in this category, achieving accuracy >90%. Furthermore, PaL seems to maintain consistent performance as the complexity of questions increases; see below. Here, we see that added complexity in the form of large numbers or more objects within a reasoning task is simple to handle programmatically, though handling such complexity directly with an LLM might cause issues.
Now from our partners!
Rebuy Engine is the Commerce AI company. They use cutting edge deep learning techniques to make any online shopping experience more personalized and enjoyable.
KUNGFU.AI partners with clients to help them compete and lead in the age of AI. Their team of AI-native experts deliver strategy, engineering, and operations services to achieve AI-centric transformation.
MosaicML enables you to easily train and deploy large AI models on your data and in your secure environment. To try out their tools and platform, sign up here! Plus, MosaicML has a tendency to release awesome open-source, commercially-usable LLMs.
Program of Thoughts (PoT) Prompting
As previously mentioned, the reasoning process with CoT prompting has two distinct steps:
Generating a language (or program)-based solution rationale
Computing the final answer according to this rationale
LLMs excel at performing the first step outlined above, but they may struggle with computing the final answer. Oftentimes, this issue occurs due to an arithmetic error or inability to evaluate a complex expression. Put simply, LLMs struggle with complex numerical tasks. In [2], authors aim to leverage a code-augmented prompting approach, called Program of Thoughts (PoT) prompting, to mitigate this issue and enable LLMs to accurately solve complex numerical tasks.
“In PoT, the computation can be delegated to a program interpreter, which is used to execute the generated program, thus decoupling complex computation from reasoning and language understanding.” - from [2]
As we might suspect, PoT prompting is quite similar to PaL. Both techniques use code-augmented prompting techniques to solve complex reasoning tasks and delegate necessary portions of the reasoning process to a code interpreter. More specifically, PoT prompting leverages few-shot learning with code-based LLMs (e.g., Codex [4]) to generate hybrid rationales that contain both natural language statements and code (in Python). Then, the code portion of the output is offloaded to an interpreter for evaluation, thus decoupling reasoning and computation.
In contrast, CoT prompting performs both reasoning and computation directly with the LLM. This is a problem because LLMs struggle to:
Perform basic arithmetic (especially with larger numbers)
Evaluate complex mathematical expressions (e.g., polynomial or differential equations)
Solve problems that require iteration
Such issues are demonstrated by the figure above, where an LLM with CoT prompting fails to evaluate a simple, cubic equation or reason over an iterative computation of the Fibonacci sequence. Luckily, we can solve these problems pretty easily with a program! For example, we can compute the Fibonacci sequence with a for loop, and a cubic equation can be easily expressed in Python syntax. Then, we can just run this program to generate the correct output, thus removing unneeded dependencies upon the LLM.
details of PoT. Similarly to PaL, PoT prompting generates problem-solving rationales that contain both language and code components. The LLM is taught how to generate such rationales via a series of few-shot exemplars that contain pairs of questions with an associated “program of thoughts” (i.e., a multi-step program with interleaved natural language statements that explain the computation); see above.
Unlike PaL, code written by PoT relies upon a symbolic math library called SymPy. This package allows the user to define mathematical “symbols”, which can then be combined together to form complex expressions. To evaluate these expressions, we can simply pass them into SymPy’s solve function; see above. For more details, check out the tutorial below.
Despite its use of symbolic math, PoT prompting is different from trying to directly generate mathematical equations with an LLM, which has been shown by prior work to be quite difficult [3]. This is because PoT prompting:
Generates symbolic equations via a multi-step, rationale-driven process.
Associates symbolic variables with semantically-meaningful names.
Similarly to PaL, authors in [2] note that assigning meaningful names to the variables in a program does measurably impact the LLM’s performance.
the results. PoT prompting is evaluated using both Codex [4] and GPT-3 [7] on several math word problem and financial question answering datasets (e.g., FinQA [8] and ConvFinQA [9]). Several different LLMs are adopted as baselines using both few-shot learning and CoT prompting (including a CoT prompting variant that is given access to an external calculator). As shown in the table below, PoT prompting outperforms baselines by a significant margin in all cases, which emphasizes the value of decoupling reasoning from computation.
Interestingly, authors in [2] also find that zero-shot PoT prompting (i.e., similar to zero-shot CoT prompting [10]) works quite well. Even without curating several examples of program-infused rationales for the LLM, we can achieve reasonable performance with an LLM on numerical tasks via PoT prompting. Additionally, the authors make an interesting practical note about using PoT prompting. To avoid generating fully language-based rationales (i.e., a program with all comments), they have to manually suppress the probability of the # token. Although this is a small detail, it is important to keep in mind—we don’t want our generated program to be nothing but comments! Plus, it demonstrates that making such techniques work in practice is oftentimes brittle and difficult.
Can we do better?
Both PaL and PoT adopt a greedy decoding strategy in a majority of experiments, meaning that the LLM will produce an output sequence by iteratively selecting the next token with the highest probability. However, there are a variety of better decoding strategies that we can use! One notable (and super simple) strategy is Self-Consistency [14]. This techniques uses the same LLM and prompt to produce multiple different outputs for a problem. Then, the final answer is derived by taking a majority vote over all outputs that are generated; see above.
When Self-Consistency is applied to PoT prompting, we see an immediate and significant benefit! As shown above, PoT with Self-Consistency achieves new state-of-the-art performance on nearly every dataset considered within [2]. Similarly, PaL [1] benefits from the use of Self-Consistency and is even used to explore more complex decoding/prompting strategies, such as least-to-most prompting [15] (i.e., a variant of CoT prompting that explicitly solves reasoning tasks one step at a time). When combined with this more sophisticated prompting style, PaL becomes even more effective; see below.
Although PaL and PoT work quite well, we can make them a little bit better with some easy-to-implement additions to their prompting technique. Such findings inspire further experimentation. Maybe we can get added performance benefits by leveraging other useful techniques, such as prompt ensembles.
Final Thoughts
Although LLMs are useful by themselves, we see in this overview that they can be a lot cooler when given access to useful tools. In particular, we have learned that connecting an LLM to an external code interpreter can be incredibly beneficial to performance on reasoning tasks. However, we need access to an LLM that is capable of writing code for this to work well. Some takeaways are outlined below.
why does this work? The effectiveness of PaL and PoT stems from the fact that LLMs are capable of generating accurate problem-solving rationales but tend to struggle with simple tasks like arithmetic and iteration. Luckily, such concepts can be easily modeled within a program, making the connection of LLMs to an external code interpreter an intuitive and powerful technique for solving reasoning problems. Put simply, we gain a lot by relying on LLMs for what they are good at and delegating remaining problem-solving components to a code interpreter than can more reliably produce a solution.
how should we solve LLM weaknesses? As briefly mentioned in this post, many of the known shortcomings of LLMs are being solved as more powerful models, such as GPT-4, are released. However, we see in this overview that alternative methods of solving such problems exist that might even be more reliable. In particular, relying upon an external code interpreter can solve issues experienced due to an LLM’s limitations in solving reasoning-based tasks. Giving a model the ability to execute code undoubtedly increases the scope of its abilities, which inspires us to think about other tools that may be useful to an LLM.
expressing thoughts as a program. This work really highlights the fact that programs can be interpreted as a structured language for expressing one’s thoughts. Compared to natural language, programming languages are more constrained, which gives them the ability to easily express iteration, model complex equations, and more. However, the formal nature of programs also limits expressivity—writing a poem is much easier in natural language than in a Python script (assuming no calls to the GPT-4 API)! Considering the differences between natural language and code is, in my opinion, pretty interesting. We see here that combining them together can draw upon the strengths of both.
New to the newsletter?
Hello! I am Cameron R. Wolfe, Director of AI at Rebuy and PhD student at Rice University. I study the empirical and theoretical foundations of deep learning. This is the Deep (Learning) Focus newsletter, where I help readers build a better understanding of deep learning research via understandable overviews that explain relevant topics from the ground up. If you like this newsletter, please subscribe, share it, or follow me on twitter!
Bibliography
[1] Gao, Luyu, et al. "PAL: Program-aided Language Models." arXiv preprint arXiv:2211.10435 (2022).
[2] Chen, Wenhu, et al. "Program of thoughts prompting: Disentangling computation from reasoning for numerical reasoning tasks." arXiv preprint arXiv:2211.12588 (2022).
[3] Wei, Jason, et al. "Chain of thought prompting elicits reasoning in large language models." arXiv preprint arXiv:2201.11903 (2022).
[4] Chen, Mark, et al. "Evaluating large language models trained on code." arXiv preprint arXiv:2107.03374 (2021).
[5] Lewkowycz, Aitor, et al. "Solving quantitative reasoning problems with language models." arXiv preprint arXiv:2206.14858 (2022).
[6] Chen, Wenhu. "Large language models are few (1)-shot table reasoners." arXiv preprint arXiv:2210.06710 (2022).
[7] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.
[8] Chen, Zhiyu, et al. "Finqa: A dataset of numerical reasoning over financial data." arXiv preprint arXiv:2109.00122 (2021).
[9] Chen, Zhiyu, et al. "Convfinqa: Exploring the chain of numerical reasoning in conversational finance question answering." arXiv preprint arXiv:2210.03849 (2022).
[10] Kojima, Takeshi, et al. "Large language models are zero-shot reasoners." arXiv preprint arXiv:2205.11916 (2022).
[11] Ouyang, Long, et al. "Training language models to follow instructions with human feedback." Advances in Neural Information Processing Systems 35 (2022): 27730-27744.
[12] Thoppilan, Romal, et al. "Lamda: Language models for dialog applications." arXiv preprint arXiv:2201.08239 (2022).
[13] Li, Yifei, et al. "On the advance of making language models better reasoners." arXiv preprint arXiv:2206.02336 (2022).
[14] Wang, Xuezhi, et al. "Self-consistency improves chain of thought reasoning in language models." arXiv preprint arXiv:2203.11171 (2022).
[15] Zhou, Denny, et al. "Least-to-most prompting enables complex reasoning in large language models." arXiv preprint arXiv:2205.10625 (2022).
[16] Press, Ofir, et al. "Measuring and Narrowing the Compositionality Gap in Language Models." arXiv preprint arXiv:2210.03350 (2022).
This was great. Thanks